다음 네 성질,property을 갖는 집합,set과 이항연산,binary_operation이 있을 경우??
(MathWorld)
closure
associativity
identity
inverse
A group is a 모노이드,monoid each of whose elements is invertible.associativity
identity
inverse
(MathWorld)
군이 되려면
{
https://encyclopediaofmath.org/wiki/Semi-group
}
조건이 추가된 가환군(아래)이 있음.
- 연산에 대해 닫혀 있다
- 결합법칙 성립
- 항등원 존재
- 역원 존재
{
https://encyclopediaofmath.org/wiki/Semi-group
}
조건이 추가된 가환군(아래)이 있음.
chk: 군은 역원을 갖는 모노이드?
TBW
대칭성,symmetry과 관련있음. 관계 서술.
잉여류,coset
{
/// local txt에 작성중
https://artofproblemsolving.com/wiki/index.php/Coset
}
대칭성,symmetry과 관련있음. 관계 서술.
잉여류,coset
{
/// local txt에 작성중
https://artofproblemsolving.com/wiki/index.php/Coset
}
Sub:
직교군,orthogonal_group
 orthogonal_group
orthogonal_group
general_orthogonal_group w GO
stable_orthogonal_group w
MKL 직교행렬,orthogonal_matrix
https://mathworld.wolfram.com/OrthogonalGroup.html
Up: 직교성,orthogonality 군,group
unitary_group
직교군,orthogonal_group
general_orthogonal_group w GO
general orthogonal group
일반직교군?
https://mathworld.wolfram.com/GeneralOrthogonalGroup.html
// general orthogonal group ... general orthogonal group
general orthogonal group  general orthogonal group
general orthogonal group
special_orthogonal_group SO일반직교군?
https://mathworld.wolfram.com/GeneralOrthogonalGroup.html
// general orthogonal group ...
special orthogonal group
특수직교군? 특별직교군?
https://mathworld.wolfram.com/SpecialOrthogonalGroup.html
 Special_orthogonal_group
Special_orthogonal_group
Sub: 회전군,rotation_group SO(3)
// special orthogonal group ... special orthogonal group
special orthogonal group  special orthogonal group
special orthogonal group
사영직교군,projective_orthogonal_group w PO특수직교군? 특별직교군?
https://mathworld.wolfram.com/SpecialOrthogonalGroup.html
Sub: 회전군,rotation_group SO(3)
// special orthogonal group ...
stable_orthogonal_group w
MKL 직교행렬,orthogonal_matrix
https://mathworld.wolfram.com/OrthogonalGroup.html
Up: 직교성,orthogonality 군,group
unitary group
 unitary_group
unitary_group
MKL 유니터리행렬,unitary_matrix
special_unitary_group
// unitary group ... unitary group
unitary group  unitary group
unitary group  unitary group
unitary group
..........CLEANUPBELOW............MKL 유니터리행렬,unitary_matrix
special_unitary_group
// unitary group ...
자명군,trivial_group
유한단순군,finite_simple_group - 이상 두개 writing
monster_group or monster_simple_group
유한군,finite_group
가해군,solvable_group - writing
초가해군,supersolvable_group
위수,order
{
}
중심,center - 군의 중심.![[https]](/123/imgs/https.png) 수학백과: 군의 중심
수학백과: 군의 중심
자기동형군,automorphism_group
{
}
치환군,permutation_group - writing
교대군,alternating_group - writing
자유군,free_group - 작성중
free_Abelian_group free_abelian_group
자유가환군 자유_아벨_군
심플렉틱군,symplectic_group
산재군,sporadic_group - 작성중
 산재군
산재군
 Sporadic_group
Sporadic_group
https://mathworld.wolfram.com/SporadicGroup.html
https://encyclopediaofmath.org/wiki/Sporadic_simple_group
https://ncatlab.org/nlab/show/sporadic finite simple group
기본군,fundamental_group - 작성중
호모토피군,homotopy_group - 작성중
Lorentz_group - writing
dihedral_group - writing
// addhere
군연산,group_operation 별도페이지필요?
군표현,group_representation
원소,element가 하나 뿐.
tmp bmks ko 가장 작은 군 https://blog.naver.com/birth1104/220289397604 - 가장 작은 군은 자명군이며 공집합,empty_set이 될 수가 없다.
 자명군
자명군
 Trivial_group - aka zero group - rel. 영,zero
Trivial_group - aka zero group - rel. 영,zero
https://mathworld.wolfram.com/TrivialGroup.html
https://ncatlab.org/nlab/show/trivial group
단순군,simple_grouptmp bmks ko 가장 작은 군 https://blog.naver.com/birth1104/220289397604 - 가장 작은 군은 자명군이며 공집합,empty_set이 될 수가 없다.
https://mathworld.wolfram.com/TrivialGroup.html
https://ncatlab.org/nlab/show/trivial group
유한단순군,finite_simple_group - 이상 두개 writing
monster_group or monster_simple_group
https://mathworld.wolfram.com/MonsterGroup.html
 Monster_group
Monster_group
 괴물군_(수학)
괴물군_(수학)
https://ncatlab.org/nlab/show/Monster group
https://groupprops.subwiki.org/wiki/Monster_group
https://proofwiki.org/wiki/Definition:Monster_Group
몫군,quotient_group(writing)https://ncatlab.org/nlab/show/Monster group
https://groupprops.subwiki.org/wiki/Monster_group
https://proofwiki.org/wiki/Definition:Monster_Group
유한군,finite_group
가해군,solvable_group - writing
초가해군,supersolvable_group
위수,order
군에 속한 원소의 개수....뿐만이 아니라 두가지 뜻이 있다고
![[https]](/123/imgs/https.png) 수학백과: 위수
수학백과: 위수
 Order_(group_theory)
Order_(group_theory)
 위수_(수학) <- aka '차수'라고도 언급
위수_(수학) <- aka '차수'라고도 언급
https://encyclopediaofmath.org/wiki/Order (군론 말고도 다양한 뜻 설명 도중에 있음)
https://ncatlab.org/nlab/show/order of a group
https://mathworld.wolfram.com/GroupOrder.html
중심화부분군, "centralizer "???![[https]](/123/imgs/https.png) 수학백과: 위수
수학백과: 위수https://encyclopediaofmath.org/wiki/Order (군론 말고도 다양한 뜻 설명 도중에 있음)
https://ncatlab.org/nlab/show/order of a group
https://mathworld.wolfram.com/GroupOrder.html
{
}
중심,center - 군의 중심.
![[https]](/123/imgs/https.png) 수학백과: 군의 중심
수학백과: 군의 중심자기동형군,automorphism_group
{
}
치환군,permutation_group - writing
교대군,alternating_group - writing
자유군,free_group - 작성중
free_Abelian_group free_abelian_group
자유가환군 자유_아벨_군
// free_commutative_group 이라는 말은 안 쓰이나? ..  free_commutative_group
free_commutative_group
![[https]](/123/imgs/https.png) 수학백과: 자유가환군
수학백과: 자유가환군
https://mathworld.wolfram.com/FreeAbelianGroup.html
 자유_아벨_군
자유_아벨_군
 Free_abelian_group
Free_abelian_group
https://encyclopediaofmath.org/wiki/Free_Abelian_group
https://ncatlab.org/nlab/show/free abelian group
tmp: 자유아벨군
자유아벨군  자유가환군
자유가환군
덧셈군, 가법군, additive_group![[https]](/123/imgs/https.png) 수학백과: 자유가환군
수학백과: 자유가환군https://mathworld.wolfram.com/FreeAbelianGroup.html
https://encyclopediaofmath.org/wiki/Free_Abelian_group
https://ncatlab.org/nlab/show/free abelian group
tmp:
아벨군의 이항 연산이 덧셈 연산인 군[1]
 가법군 { 덧셈에 대하여 닫혀 있고, 결합 법칙과 교환 법칙이 성립하는 군 }
가법군 { 덧셈에 대하여 닫혀 있고, 결합 법칙과 교환 법칙이 성립하는 군 }
 Additive_group
Additive_group
mklink: 가법성,additivity
곱셈군,multiplicative_group - 작성중mklink: 가법성,additivity
= 승법군
 Multiplicative_group
Multiplicative_group
https://mathworld.wolfram.com/MultiplicativeGroup.html
https://everything2.com/title/multiplicative group
mklink 곱셈,multiplication
리_군,Lie_group - 작성중https://mathworld.wolfram.com/MultiplicativeGroup.html
https://everything2.com/title/multiplicative group
mklink 곱셈,multiplication
심플렉틱군,symplectic_group
https://mathworld.wolfram.com/SymplecticGroup.html
https://encyclopediaofmath.org/wiki/Symplectic_group
선형군,linear_group - 작성중https://encyclopediaofmath.org/wiki/Symplectic_group
산재군,sporadic_group - 작성중
https://mathworld.wolfram.com/SporadicGroup.html
https://encyclopediaofmath.org/wiki/Sporadic_simple_group
https://ncatlab.org/nlab/show/sporadic finite simple group
호모토피군,homotopy_group - 작성중
Lorentz_group - writing
dihedral_group - writing
// addhere
군연산,group_operation 별도페이지필요?
군표현,group_representation
1. 정의 ¶
연산,operation *를 가지고 있는 공집합이 아닌 집합 G에 대해, 다음 성질
중에서 G1~G3을 만족하면 군이라고 한다.
| 전제 | 성질 | 성질의 명칭 | |
| G1 | ∀a,b,c∈G | (a*b)*c=(a*b)*c | 결합법칙,associativity |
| G2 | ∀a∈G | ∃e∈G such that e*a=a*e=a | 항등원,identity_element e의 존재 |
| G3 | ∀a∈G | ∃a'∈G such that a'*a=a*a'=e | 역원,inverse_element a'의 존재 |
| G4 | ∀a,b∈G | a*b=b*a | 교환법칙,commutativity |
군이 G4를 만족하면 가환군이고,
가환군이 아닌 군은 비가환군이다.
(고급수학.pdf p24)가환군이 아닌 군은 비가환군이다.
◆를 집합 G에 대한 이항연산,binary_operation이라고 하자.
(이것은 ∀x,y∈G ⇒ x◆y∈G이고, x◆y는 오직 하나로 결정된다는 뜻.)
G가 연산 ◆과 함께 다음 성질을 만족하면, G 또는 (G, ◆)를 군이라고 한다.
(이것은 ∀x,y∈G ⇒ x◆y∈G이고, x◆y는 오직 하나로 결정된다는 뜻.)
G가 연산 ◆과 함께 다음 성질을 만족하면, G 또는 (G, ◆)를 군이라고 한다.
- x,y,z∈G ⇒ x◆(y◆z)=(x◆y)◆z
즉 ◆에 대한 결합법칙이 성립.
- 다음 성질을 만족하는 e∈G가 존재한다.
∀x∈G, e◆x=x◆e=x
여기서 e는 항등원이다.
- 각각의 x∈G에 대해 다음 성질을 만족하는 x-1∈G가 존재한다.
x◆x-1=x-1◆x=e
즉 x는 역원을 갖는다.
- 그리고 만일 다음이 성립하면 G는 가환군 또는 아벨군이라 부른다.
x,y∈G ⇒ x◆y=y◆x
(◆에 대한 교환법칙이 성립한다.)
(ℤ, +), (ℚ, +)는 군이다.
(ℕ, +)는 군이 아니다. (∵ 덧셈에 대한 역원이 없음)
(10개의 특강으로 끝내는 수학의 기본 원리 p212)(ℕ, +)는 군이 아니다. (∵ 덧셈에 대한 역원이 없음)
2.1. 대칭군 ¶
curr goto 대칭성,symmetry
pagename 영어로 구분되긴 하지만... 각각 대칭적군 대칭성군 이러면 어떨까
// 이건 기하학의 군?? chk
// from https://horizon.kias.re.kr/17080/ 위에서 30% 쯤 그림 바로 뒤
{
어떤 집합 에 작용하는 대칭군
에 작용하는 대칭군 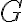 란, 집합
란, 집합  에서 자신으로 가는 일대일대응(전단사,bijection, 전단사함수,bijective_function)들의 집합인데
에서 자신으로 가는 일대일대응(전단사,bijection, 전단사함수,bijective_function)들의 집합인데
// from https://horizon.kias.re.kr/17080/ 위에서 30% 쯤 그림 바로 뒤
{
어떤 집합
- 두 원소를 합성,composition하면 다시
의 원소가 되고,
의 원소들의 역함수,inverse_function들이 모두
에 포함되고,
- 항등함수,identity_function가
에 포함되는
2.1.2. 대칭군 symmetry group ¶
2.2. 부분군 subgroup ¶
부분군,subgroup - 작성중 https://artofproblemsolving.com/wiki/index.php/Subgroup
정규부분군,normal_subgroup - 작성중 https://artofproblemsolving.com/wiki/index.php/Normal_subgroup
순환부분군,cyclic_subgroup
characteristic_subgroup
정규부분군,normal_subgroup - 작성중 https://artofproblemsolving.com/wiki/index.php/Normal_subgroup
순환부분군,cyclic_subgroup
characteristic_subgroup
// (이하 순환-가환-멱영-가해 군은 먼저 것이 다음 것에 포함되며 같지 않음.)
- 순환군 ⊊ 가환군 ⊊ 멱영군 ⊊ 가해군 ? chk
- 순환군 ⊊ 가환군 ⊊ 멱영군 ⊊ 가해군 ? chk
2.4. 가환군 commutative group, 아벨 군 abelian group ¶
mkl free_abelian_group
mkl 비아벨군 - non-abelian_group
https://mathworld.wolfram.com/AbelianGroup.html
mkl 비아벨군 - non-abelian_group
https://mathworld.wolfram.com/AbelianGroup.html
4. Links ko ¶
정석(6차 수I p22)
집합,set G에 연산 ⚬가 정의되어 있어 ⑴~⑷ 조건을 만족시키면 G는 연산 ⚬에 대한 군, ⑴~⑸ 조건을 만족시키면 G는 연산 ⚬에 대한 가환군.
⑴ 연산에 대해 닫혀 있음
집합,set G에 연산 ⚬가 정의되어 있어 ⑴~⑷ 조건을 만족시키면 G는 연산 ⚬에 대한 군, ⑴~⑸ 조건을 만족시키면 G는 연산 ⚬에 대한 가환군.
⑴ 연산에 대해 닫혀 있음
a ∈ G, b ∈ G 이면 a ⚬ b ∈ G
⑵ 결합법칙 성립∀ a, b, c ∈ G,
(a ⚬ b) ⚬ c = a ⚬ (b ⚬ c)
⑶ 항등원 존재(a ⚬ b) ⚬ c = a ⚬ (b ⚬ c)
∀ a ∈ G,
∃ e ∈ G such that
a ⚬ e = e ⚬ a = a
(e: 연산 ⚬에 대한 항등원)
⑷ 역원 존재∃ e ∈ G such that
a ⚬ e = e ⚬ a = a
(e: 연산 ⚬에 대한 항등원)
∀ a ∈ G,
∃ x ∈ G such that
a ⚬ x = x ⚬ a = e
(x: ⚬에 대한 a의 역원, e: 항등원)
⑸ 교환법칙 성립∃ x ∈ G such that
a ⚬ x = x ⚬ a = e
(x: ⚬에 대한 a의 역원, e: 항등원)
∀ a, b ∈ G,
a ⚬ b = b ⚬ a
a ⚬ b = b ⚬ a
6. Etc ¶
group의 다른 뜻, tmp
통계,statistics 특히 가설검정,hypothesis_test에서 group은 실험군(실험집단) 대조군(통제집단) 할 때 그 군/집단. 둘의 차이는 독립변인 or 독립변수,independent_variable.
통계,statistics 특히 가설검정,hypothesis_test에서 group은 실험군(실험집단) 대조군(통제집단) 할 때 그 군/집단. 둘의 차이는 독립변인 or 독립변수,independent_variable.
- 통제집단 control group = 대조군 - 실험이나 처치(treatment)를 하지 않은 집단
- 실험집단 experimental group = 실험군 = 처치집단 ...
![[https]](/123/imgs/https.png) 두산백과: 실험 집단 experimental group
두산백과: 실험 집단 experimental group
Twins:
https://artofproblemsolving.com/wiki/index.php/Group
https://mathworld.wolfram.com/Group.html
 Group_(mathematics)
Group_(mathematics)
 Group_theory
Group_theory
![[https]](/123/imgs/https.png) https://en.citizendium.org/wiki/Group_(mathematics)
https://en.citizendium.org/wiki/Group_(mathematics)
![[https]](/123/imgs/https.png) https://en.citizendium.org/wiki/Group_theory
https://en.citizendium.org/wiki/Group_theory
https://ncatlab.org/nlab/show/group
http://foldoc.org/group
https://everything2.com/title/group (다른것 많이 포함)
https://everything2.com/title/group theory
https://proofwiki.org/wiki/Definition:Group
https://artofproblemsolving.com/wiki/index.php/Group
https://mathworld.wolfram.com/Group.html
![[https]](/123/imgs/https.png) https://en.citizendium.org/wiki/Group_(mathematics)
https://en.citizendium.org/wiki/Group_(mathematics)![[https]](/123/imgs/https.png) https://en.citizendium.org/wiki/Group_theory
https://en.citizendium.org/wiki/Group_theoryhttps://ncatlab.org/nlab/show/group
http://foldoc.org/group
https://everything2.com/title/group (다른것 많이 포함)
https://everything2.com/title/group theory
https://proofwiki.org/wiki/Definition:Group
안정자,stabilizer
kms stabilizer : 안정자 ... https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=stabilizer
https://artofproblemsolving.com/wiki/index.php/Stabilizer
kms stabilizer : 안정자 ... https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=stabilizer
https://artofproblemsolving.com/wiki/index.php/Stabilizer
Sylow_theorem
kms sylow : 실로우 ... https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=sylow
https://artofproblemsolving.com/wiki/index.php/Sylow_Theorems
}
kms sylow : 실로우 ... https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=sylow
https://artofproblemsolving.com/wiki/index.php/Sylow_Theorems
}
Up: 대수학,algebra

