의 뜻:
if
극한값은 함수값이나 함수값의 존재 여부와는 무관.
극한이 존재하려면 좌극한과 우극한이 같아야 함.
극한이 존재하려면 좌극한과 우극한이 같아야 함.
즉 극한값의 존재 여부(존재성,existence)를 따질 때, 극한값이 없다는 것을 보이려면 좌극한과 우극한이 다름을 보이면 됨. - 또는 물론 좌극한이 없다거나, ...etc. - 모두 찾아서 정리.
극한값이 없는 다른 경우들 TBW
cmp 함수값 / tbw 함수값과 극한값이 다른, ...etc. 극한값 문단 mk? 극한값
극한값  극한값
극한값  극한값
극한값  극한값
극한값
TBD 함수값,function_value과 비교 용도로 극한값 page분리할필요 있는지? page 극한값,limit_value? 영어로 맞는 표현? 글쎄?? 필요없을듯하긴 한데.. 극한,limit 값,value
관련: 점근선,asymptote(curr go 직선,line)cmp 함수값 / tbw 함수값과 극한값이 다른, ...etc. 극한값 문단 mk?
TBD 함수값,function_value과 비교 용도로 극한값 page분리할필요 있는지? page 극한값,limit_value? 영어로 맞는 표현? 글쎄?? 필요없을듯하긴 한데.. 극한,limit 값,value
2. Limit laws ¶
단 n은 양의 정수.
3. 무한대,infinity관련 극한 ¶
이건 어떻게 보면 매우 오래된(고대 그리스) 개념인데, 미적분학의 역사의 극 초반에 언급되는 내용. method of exhaustion.
어떤 원,circle 안에 들어가는 n각형(다각형,polygon)의 넓이,area가) 이면
이면
=) 원의 면적
원의 면적
또는
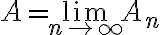
극한에 도달하지 못했다면 근사,approximation와 관련.
어떤 원,circle 안에 들어가는 n각형(다각형,polygon)의 넓이,area가
iff
such that
iff
such that
from Stewart
Let  be a function defined on some open 구간,interval that contains the number
be a function defined on some open 구간,interval that contains the number  , except possibly at
, except possibly at  itself. Then
itself. Then
=\infty)
means that for every positive number 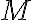 there is a positive number
there is a positive number 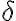 such that
such that
=-\infty)
의 뜻은, 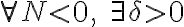 such that
such that
<N)
Let  be a function defined on some interval
be a function defined on some interval .) Then
Then
=\infty)
means that for every positive number 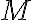 there is a corresponding positive number
there is a corresponding positive number 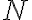 such that
such that
if 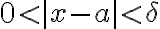 then
then >M)
마찬가지로if 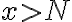 then
then >M)
Def.
⇔
4. Limits At Infinity ¶
Fact:
1. 이 양의 유리수,rational_number이고 c가 임의의 실수이면,
이 양의 유리수,rational_number이고 c가 임의의 실수이면,

2.  이 양의 유리수,rational_number이고 c가 임의의 실수이고
이 양의 유리수,rational_number이고 c가 임의의 실수이고 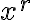 이
이 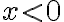 에서 정의되었으면,
에서 정의되었으면,
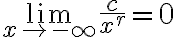
from https://tutorial.math.lamar.edu/Classes/CalcI/LimitsAtInfinityI.aspx
1.
5. 수열의 극한 ¶
(보통 함수,function의 극한을 얘기하는데 -  함수의_극한) 여기선 수열,sequence의 극한을... (Q1. 함수 수열 말고 다른 극한이 있는지? Q2. 이 둘을 어떻게 체계적으로 re-write할 것인지)
함수의_극한) 여기선 수열,sequence의 극한을... (Q1. 함수 수열 말고 다른 극한이 있는지? Q2. 이 둘을 어떻게 체계적으로 re-write할 것인지)
The limit of a sequence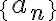 is
is 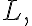 written
written

if, for each 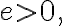 there is an integer
there is an integer 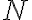 such that
such that 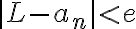 whenever
whenever 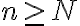 .
.
The limit of a sequence
수열의 극한이 존재하면 convergent; otherwise, divergent.
// from http://archives.math.utk.edu/visual.calculus/6/sequences.3/index.html
// from http://archives.math.utk.edu/visual.calculus/6/sequences.3/index.html
정의
수열 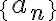 이
이 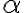 에 수렴한다 ⇔
에 수렴한다 ⇔
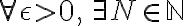 such that
such that 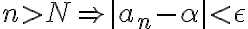
수열 {an}이 α에 수렴한다는 것은
임의의 양수 ε에 대해 자연수 N이 존재하여
n>N일 때 마다 |an-α|<ε이 성립하는 것.
임의의 양수 ε에 대해 자연수 N이 존재하여
n>N일 때 마다 |an-α|<ε이 성립하는 것.
12. 영단어 limit의 다른 뜻 ¶
극한_EpsilonDeltaLimitDefinition
미적분,calculus
수열,sequence이 극한값을 가진다면 수렴한다(converge)고 하고 수렴하는(convergent) 수열이라고 한다.
수렴하지 않을 때는 발산하는(divergent) 수열이라고 말한다.
https://calculus.subwiki.org/wiki/Limithttps://everything2.com/title/limit
https://mathworld.wolfram.com/Limit.html
Up: 해석학,analysis


![[https]](/123/imgs/https.png)