극한의 엄밀한 정의: ε-δ를 이용한
Formal definition of limits
Formal definition of limits
아님 특정 점으로 수렴,convergence하는 극한은 ε-δ, 무한대로 가는(발산,divergence?) 극한 관련되면 ε-N?
아주작은양수(실수) δ, 아주큰자연수 N 같은데...?
아주작은양수(실수) δ, 아주큰자연수 N 같은데...?
1. Links ¶
https://blog.naver.com/dydrogud22/110188882533
https://blog.naver.com/dydrogud22/110188927079
https://blog.naver.com/dydrogud22/110188937447
https://blog.naver.com/dydrogud22/110188927079
https://blog.naver.com/dydrogud22/110188937447
Twins:
 엡실론-델타_논법
엡실론-델타_논법
 미적분학#극한의_정의
미적분학#극한의_정의
![[https]](/123/imgs/https.png) https://en.wikipedia.org/wiki/(%CE%B5,_%CE%B4)-definition_of_limit redir to
https://en.wikipedia.org/wiki/(%CE%B5,_%CE%B4)-definition_of_limit redir to  Limit_of_a_function#Functions_of_a_single_variable
Limit_of_a_function#Functions_of_a_single_variable
![[https]](/123/imgs/https.png) https://en.wikipedia.org/wiki/(%CE%B5,_%CE%B4)-definition_of_limit redir to
https://en.wikipedia.org/wiki/(%CE%B5,_%CE%B4)-definition_of_limit redir to 나올 수 밖에 없는 타이밍. 입실론 델타의 정석 - 수학 갤러리
http://gall.dcinside.com/board/view/?id=mathematics&no=48306
copy at
http://yeogue.tistory.com/300
http://gall.dcinside.com/board/view/?id=mathematics&no=48306
copy at
http://yeogue.tistory.com/300
3. 정의 ¶
limx→af(x) = L
임의의 실수 ϵ>0에 대해, 적당한 실수 δ>0 가 존재해서, 0<∣x−a∣<δ ⇒ ∣f(x)−L∣<ϵ 이다
임의의 실수 ϵ>0에 대해, 적당한 실수 δ>0 가 존재해서, 0<∣x−a∣<δ ⇒ ∣f(x)−L∣<ϵ 이다
임의의 실수
δ는 ε에 영향을 받는 변수이다. δ = δ(ε)
f(a)가 반드시 정의될 필요는 없다. 따라서 0<|x-a|<δ 의 0< 부분이 있는 것.
먼저
 : 상수
: 상수
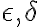 : 매우 작은 양수
: 매우 작은 양수
 : 변수
: 변수
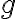 : 함수
: 함수
* * *
"g(x)에서 x가 a에 가까이 가면, g(x)는 L에 가까이 간다"를 식으로 표현하면
=L)
위 명제가 성립할 필요충분조건은
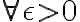 에 대해 어떤 수
에 대해 어떤 수 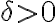 가 존재하여 다음을 만족한다.
가 존재하여 다음을 만족한다.
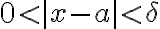 이면
이면 -L|<\epsilon) 이다.
이다.
x가 a로 가까이 가지만 결코 a와 같을 수 없다.
하지만=L) 일 가능성은 배제하지 않는다.
일 가능성은 배제하지 않는다.
실제로 이렇게 가정하면, 즉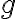 가 상수함수라면,
가 상수함수라면,
-L|=|L-L|=0<\epsilon)
이므로 -L|<\epsilon) 은 항상 성립한다.
은 항상 성립한다.
그럼 임의의 함수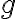 에 대해 성립함을 보이려면 무엇을 해야 하는가?
에 대해 성립함을 보이려면 무엇을 해야 하는가?
하지만
실제로 이렇게 가정하면, 즉
그럼 임의의 함수
정의에 따라, 주어진 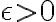 에 대해 다음 명제를 만족하는 어떤 수
에 대해 다음 명제를 만족하는 어떤 수 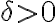 를 만들어야 할 것이다.
를 만들어야 할 것이다.
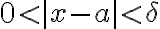 이면
이면 -L|<\epsilon) 이다.
이다.
그러므로,
ε>0은 미리 주어져 있고
δ>0 값은 만들어 내야만 한다.
ε>0은 미리 주어져 있고
δ>0 값은 만들어 내야만 한다.
x가 a로 충분히 가까이 (δ보다 작은 거리로) 갈 때, (a가 되지는 않음)
g(x)도 얼마든지 L에 가까이 (ε보다 작은 거리로) 갈 수 있음을 보여야만 한다.
g(x)도 얼마든지 L에 가까이 (ε보다 작은 거리로) 갈 수 있음을 보여야만 한다.
| L에 가까이 간다는 것 | ε>0에 의해 측정됨 | ε은 누군가로부터 주어짐 |
| a에 가까이 간다는 것 | δ>0에 의해 측정됨 | δ는 우리가 만드는 것 |
(우리가 발견해야 할 값인) δ는
(우리에게 주어진 값인) ε에 따라 다른 값을 취할 수 있음을 이제는 예상할 수 있다.
"매우 작은 값인 ε"이, 일반적으로
"매우 작은 값인 δ"를 필요로 함을 예상할 수 있다.
"매우 작은 값인 δ"를 필요로 함을 예상할 수 있다.
만일 위 (극한의) 정의를 성립하는 단 하나의 δ>0 이 존재한다면,
이 정의를 성립하도록 하는 무수히 많은 값들이 존재한다.
이 정의를 성립하도록 하는 무수히 많은 값들이 존재한다.
예를 들어 (위 극한의 정의를 만족하는) δ를 발견했다고 가정하자.
그리고 δ1을 δ보다 작은 임의의 양수라고 하자. 다시 말해
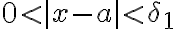 일 때
일 때 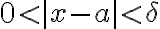 이다.
이다.
그러므로-L|<\epsilon) 이다. 따라서 δ1도 정의를 만족시킨다.
이다. 따라서 δ1도 정의를 만족시킨다.
다시 말하면, δ는 선택의 폭이 넓다.
(예를 들어 δ1=δ/2 또는 δ/3 등등)
그리고 δ1을 δ보다 작은 임의의 양수라고 하자. 다시 말해
0 < δ1 < δ
그러면 그러므로
다시 말하면, δ는 선택의 폭이 넓다.
(예를 들어 δ1=δ/2 또는 δ/3 등등)
* * *
예: 다음 식 증명.
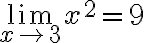
정의에 따라, 주어진 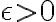 에 대해 다음을 만족하는
에 대해 다음을 만족하는 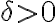 가 있음을 증명하면 됨.
가 있음을 증명하면 됨.
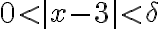 이면
이면 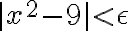 이다.
이다.
(생각보다 간단하지 않고 길어져서 생략. 절대부등식과 min함수 필요.)
// from 10개의 특강...에서 요약
4. 비유 ¶
내친구가 예전에 했던 적절한 비유인데 이게 존나 그럴싸함
입델을 하나의 게임처럼 생각하는거지
갑과 을이 게임을 하며 각각의 역할은 다음과 같아
갑 : 을에게 양수 ε(입실론) 값을 아무렇게나 던져줌
을 : 갑에게 받은 ε값을 가지고 다음 명제 만족하는 δ값을 아무거나 하나 찾아내서 갑에게 돌려줌
다음 명제 : 0<|x-a|<δ 이면 |f(x)-L|<ε이다
을 : 갑에게 받은 ε값을 가지고 다음 명제 만족하는 δ값을 아무거나 하나 찾아내서 갑에게 돌려줌
다음 명제 : 0<|x-a|<δ 이면 |f(x)-L|<ε이다
만약 을이 대답할 수 없는 ε값을 갑이 던져주면 갑의승리
갑이 무슨짓을해도 을이 수비할수있으면 을의승리
갑이 무슨짓을해도 을이 수비할수있으면 을의승리
갑이 이기면 x->a에서 f(x)의 극한은 존재하지 않음
을이 이기면 x->a에서 f(x)의 극한은 L
을이 이기면 x->a에서 f(x)의 극한은 L
물론 비유니까, 뭐 갑이 모든 양의실수를 다 말할 수 없네 어쩌네 하는 태클은 사양
8. 다변수함수의 극한 ¶
일변수함수의 극한
such that
이변수함수의 극한
의 정의는
such that
즉 작은 원 안에 들어가야 함
3변수함수의 극한은 작은 구 안에 들어가야 할 것이다? CHK
Ex.
\to(0,0)}\frac{x^2-y^2}{x^2+y^2}=?)
x축을 따라서 원점으로 갈 때 (y를 0으로 고정)
\to(0,0)}\frac{x^2-0^2}{x^2+0^2}=1)
y축을 따라서 원점으로 갈 때 (x를 0으로 고정)
\to(0,0)}\frac{0^2-y^2}{0^2+y^2}=-1)
따라서 극한은 존재하지 않음
10. 일반수학2 단국대학교 김도형 ¶
1강
⇔
∀ε>0, ∃N>0 s.t. ⇔
∀n>0, ∃N>0 such that 함수 f가 L에서 연속
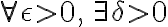
such that
-f(L)|<\epsilon)
such that
https://mathworld.wolfram.com/Epsilon-DeltaDefinition.html
https://mathworld.wolfram.com/Epsilon-DeltaProof.html
 엡실론-델타_논법
엡실론-델타_논법
https://mathworld.wolfram.com/Epsilon-DeltaProof.html


![[http]](/123/imgs/http.png)