차원,dimension에 따라,
1D에선 기울기,slope??
2D에선
 \hat{\rm i} + \frac{\partial}{\partial y}f(x,y)\hat{\rm j})
3D에선
nD에선
)
수식에서 델,del,나블라,nabla 바로 뒤에 스칼라장을 붙이면 그 스칼라장의 기울기임. 결과는 벡터장.
1D에선 기울기,slope??
2D에선
nD에선
미분가능한 다변수 스칼라값함수 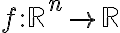 의 gradient
의 gradient 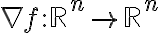 는 점,point
는 점,point ) 에서 다음 벡터,vector로 정의. (Wikipedia Gradient)
에서 다음 벡터,vector로 정의. (Wikipedia Gradient)
=\begin{bmatrix}\frac{\partial f}{\partial x_1}(p)\\ \vdots\\ \frac{\partial f}{\partial x_n}(p)\end{bmatrix})
또는 이렇게도 표기 (source: Function_of_several_real_variables#Multivariable_differentiability)
Function_of_several_real_variables#Multivariable_differentiability)
 = \left(\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}, \cdots, \frac{\partial}{\partial x_n} \right) f(\vec{x}))
아무튼 그래서 일반적으로 델,del,나블라,nabla는또는 이렇게도 표기 (source:
chk:
 가 있을 때
가 있을 때
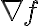 : gradient of
: gradient of  는 가장 가파르게 / 최대로 증가,increment하는 방향,direction, -> 기울기상승,gradient_ascent
는 가장 가파르게 / 최대로 증가,increment하는 방향,direction, -> 기울기상승,gradient_ascent
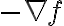 : 거기에 음의 부호를 붙이면 가장 가파르게 / 최대로 감소,decrement하는 방향? -> 기울기하강,gradient_descent
: 거기에 음의 부호를 붙이면 가장 가파르게 / 최대로 감소,decrement하는 방향? -> 기울기하강,gradient_descent
// rel. 증감,increment_and_decrement
스칼라장,scalar_field의 기울기는 최대 공간증가율의 크기와 방향을 동시에 나타내는 벡터,vector이다. (벡터? 벡터장?) (Sadiku 3.5)
입력: 스칼라장,scalar_field
출력: 벡터장,vector_field
// rel. 증감,increment_and_decrement
CHK
스칼라장을 벡터장으로? 항상?입력: 스칼라장,scalar_field
출력: 벡터장,vector_field
다변수함수의 편미분,partial_derivative과 밀접
Q: 기울기,slope와의 관계는?? slope를 더 높은 차원으로 일반화한게 gradient??
{
경사(gradient)라는 이름은, 예를 들어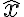 성분
성분 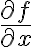 가
가  의
의  에 대한 기울기(slope)라는 점에서 비롯된 것. [1]
에 대한 기울기(slope)라는 점에서 비롯된 것. [1]
{
경사(gradient)라는 이름은, 예를 들어
각 방향/축? 에 대해 편미분을 한 다음 모아서 벡터로 만드는 것
쉬운 예:=x^2\sin y) 이면
이면
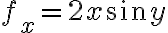
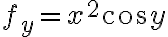
=(2x\sin y, x^2\cos y)) ← gradient
← gradient
)
Q: f 뒤에 parameter (x,y) 있는지 없는지 여부에 따라 달라지는 게 있음? 다시말해 위의 둘은 완전히 같은건가 아님 표기에 따라 차이가 있나?
쉬운 예:
Q: f 뒤에 parameter (x,y) 있는지 없는지 여부에 따라 달라지는 게 있음? 다시말해 위의 둘은 완전히 같은건가 아님 표기에 따라 차이가 있나?
기호 읽기: ∇f: del f, (nabla f,) gradient f
Contents
1. 정길수 ¶
공간상의 한 임의의 점 (x,y,z) 에서 각 방향의 기울기를 생각하면
) 의 최대 기울기는 벡터 합
의 최대 기울기는 벡터 합
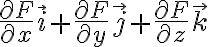
가 된다.
F)
grad F는 각 축의 기울기 중에서 최대로 급한 경사를 선택한 것이므로 전체 기울기도 최대로 급한 경사를 나타낸다.
F(x,y,z)의 x축 방향 기울기 ∂F/∂x에 방향을 생각하면 (∂F/∂x)i 가 되고
F(x,y,z)의 y축 방향 기울기 ∂F/∂y에 방향을 생각하면 (∂F/∂y)j 가 되고
F(x,y,z)의 z축 방향 기울기 ∂F/∂z에 방향을 생각하면 (∂F/∂z)k 가 된다.
따라서 F(x,y,z)의 y축 방향 기울기 ∂F/∂y에 방향을 생각하면 (∂F/∂y)j 가 되고
F(x,y,z)의 z축 방향 기울기 ∂F/∂z에 방향을 생각하면 (∂F/∂z)k 가 된다.
3. 공식 (Sadiku 식 3.31 a-d) ¶
또는 스칼라장 V의 기울기는 다음 기본 성질을 가지고 있다.
- ∇V의 크기는 단위길이당 V의 최대 변화율과 같다.
- ∇V는 V의 최대 변화율의 방향을 가리킨다.
- 임의의 점에서의 ∇V는 이 점을 지나는 V가 일정한 면에 수직이다.
- 단위벡터,unit_vector a 방향으로의 투영(또는 성분)(see 사영,projection)은 ∇V·a이고, 이것을 a에 따른 V의 방향성 도함수라 한다. (see 방향도함수,directional_derivative) 이것은 a방향에서의 V의 변화율이다. (중략) 그러므로 스칼라 함수 V의 기울기로부터 V가 가장 급격하게 변하는 방향과 V의 최대 방향성 도함수의 크기를 알 수 있다.
- 만약 A=∇V이면 V를 A의 스칼라 포텐셜이라 한다. (maybe related to 퍼텐셜,potential, curr see 스칼라,scalar, ...)
4. 공식 (Thomas) ¶
두 함수  와
와 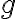 의 gradient를 알고 있으면, 그 함수들의 합(합,sum), 차(차이,difference), 곱(곱,product), 몫(몫,quotient)의 gradient를 구하는 방법.
의 gradient를 알고 있으면, 그 함수들의 합(합,sum), 차(차이,difference), 곱(곱,product), 몫(몫,quotient)의 gradient를 구하는 방법.
기울기에 대한 대수 공식
=\nabla f + \nabla g)
=\nabla f - \nabla g)
=k\nabla f) (k는 임의의 실수)
(k는 임의의 실수)
=f\nabla g + g\nabla f)
=\frac{g\nabla f-f\nabla g}{g^2})
rel. 델,del,나블라,nabla
6.1. electric potential gradient ¶
전위경도, Electric Potential Gradient (EPG?) 라는 게 있음. electric_potential_gradient  electric.potential.gradient
electric.potential.gradient
curr goto 전위,electric_potential#s-25
curr goto 전위,electric_potential#s-25
7. ML, NN, backprop에 나오는 각종 gradient ¶
신경망,neural_network (esp ANN)
오차역전파 = 역전파,backpropagation
에 나오는 gradients 일단 여기에.
물론 계산그래프,computational_graph 자동미분,automatic_differentiation 관련.
오차역전파 = 역전파,backpropagation
에 나오는 gradients 일단 여기에.
물론 계산그래프,computational_graph 자동미분,automatic_differentiation 관련.
자료들의 source는 Stanford cs231n이 대부분인 듯. https://cs231n.github.io/optimization-2/ etc.
7.1. numerical gradient vs analytic gradient ¶
10. tmp CHK ¶
직각좌표계에서 스칼라장 V의 미분,differential은
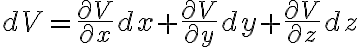
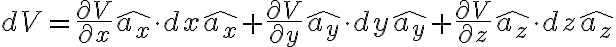
 \cdot \left( dx\hat{a_x}+dy\hat{a_y}+dz\hat{a_z} \right))
스칼라장 V의 기울기 : 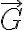 라 하면
라 하면
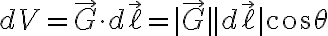
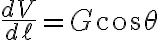 ........이 값은
........이 값은 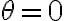 일 때 최대, 즉
일 때 최대, 즉 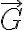 와
와 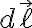 이 같은 방향일 때 최대
이 같은 방향일 때 최대
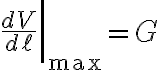
from https://www.youtube.com/watch?v=-l0gZfn1IVo&list=PL4kNQgnipU2H6NbkZDdsM4qmmVOSILnw3&index=21
11. tmp; 증감(증가/감소)와의 관계 ... mklink: 증가감소 ¶
https://sdolnote.tistory.com/entry/Gradient (very easy, 하지만 증가감소와 관련된 직관에 도움)
gradient의 방향,direction은 함수,function가 증가,increment하는 방향. viz 함수값이 커지는 방향.
{
rel. 증감,increment_and_decrement - 증가,increment and 감소,decrement
gradient의 방향,direction은 함수,function가 증가,increment하는 방향. viz 함수값이 커지는 방향.
rel. gradient의 방향이란 기울기벡터(gradient_vector)의 방향과 같은 말인지? 아님 기울기벡터가 기울기와 원래 동의어이고 뉘앙스만(뒤에 -벡터,vector 수식어가 붙었는지 아닌지만) 다른 건지? 암튼 see also 기울기벡터,gradient_vector#s-2의 선형계획법 example
chk (내생각){
rel. 증감,increment_and_decrement - 증가,increment and 감소,decrement
2d 곡선,curve function/graph에선
기울기,slope의
부호,sign는 양positive이면 증가하는 / 음negative이면 감소하는 - rel. 1st order 미분,derivative(first_order_derivative)
3d(이상) 곡면,surface(초곡면,hypersurface) function/graph에선부호,sign는 양positive이면 증가하는 / 음negative이면 감소하는 - rel. 1st order 미분,derivative(first_order_derivative)
기울기,gradient(기울기벡터,gradient_vector)의
방향,direction은 증가하는 방향이며, 그것에 마이너스 부호를 붙이면 (i.e. 방향을 반대로 하면) 감소하는 방향
}방향,direction은 증가하는 방향이며, 그것에 마이너스 부호를 붙이면 (i.e. 방향을 반대로 하면) 감소하는 방향
12. etc ¶
gradient는 ![[http]](/123/imgs/http.png) contour plot/map/curve,
contour plot/map/curve, ![[http]](/123/imgs/http.png) 등고선 과 관련있는데 TBW.
등고선 과 관련있는데 TBW.
https://math.fandom.com/wiki/Gradient
![[http]](/123/imgs/http.png) contour plot/map/curve,
contour plot/map/curve, ![[http]](/123/imgs/http.png) 등고선 과 관련있는데 TBW.
등고선 과 관련있는데 TBW.벡터가 등고선에 수직. perpendicular to the contour line.
그 벡터는 steepest descent/ascent를 가리키는.
또, gradient도 always perpendicular to the contour line.
tmp bmks en그 벡터는 steepest descent/ascent를 가리키는.
또, gradient도 always perpendicular to the contour line.
https://math.fandom.com/wiki/Gradient
AKA 그레이디언트, 그래디언트, 경사, 경사도, 경도, 변화도, 구배, 물매
Twins:  기울기_(벡터)
기울기_(벡터)
{
기울기란, 스칼라장의 최대의 증가율을 나타내는 벡터장이라 함.
}
 Gradient
Gradient
{
기울기란, 스칼라장의 최대의 증가율을 나타내는 벡터장이라 함.
}
스칼라장의 기울기(gradient) https://angeloyeo.github.io/2019/08/25/gradient.html
구배(勾配, Gradient)의 의미 https://ghebook.blogspot.com/2010/07/gradient.html
https://everything2.com/title/Gradient구배(勾配, Gradient)의 의미 https://ghebook.blogspot.com/2010/07/gradient.html
----
- [1] f의 x에 대한 기울기라는 점에서 비롯된 것이다. https://terms.naver.com/entry.nhn?docId=3578284&cid=58944&categoryId=58968


![[https]](/123/imgs/https.png)