Sub:
Excerpts
정의 7.11: 직교 기저와 직교 정규 기저
 차원 실수 유클리드 공간에 대한 기저
차원 실수 유클리드 공간에 대한 기저 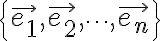 을 이루는 벡터가 모두 서로 직교하면,
을 이루는 벡터가 모두 서로 직교하면,
즉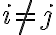 일 때
일 때 =0) 을 만족하면 // 내적,inner_product이 영,zero
을 만족하면 // 내적,inner_product이 영,zero
기저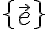 는 직교 기저라고 한다.
는 직교 기저라고 한다.
나아가 기저를 이루는 모든 벡터의 길이가 1이면, // 길이,length 하나,one 단위,unit
즉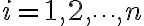 에 대해
에 대해 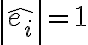 이 성립하면,
이 성립하면,
기저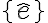 는 직교 정규 기저라고 한다. // orthonormal_basis
는 직교 정규 기저라고 한다. // orthonormal_basis
기저함수,basis_function - curr see 기저,basis#s-6
basis_change or ,change_of_basis 기저바꾸기? 기저바꿈? 기저변환? - pagename TBD, writing
순서기저,ordered_basis - writing ... 특성상 보통 복수형 ordered_bases 가 많이 보임
직교기저,orthogonal_basis - writing (see also 기저,basis#s-2)
{basis_change or ,change_of_basis 기저바꾸기? 기저바꿈? 기저변환? - pagename TBD, writing
순서기저,ordered_basis - writing ... 특성상 보통 복수형 ordered_bases 가 많이 보임
직교기저,orthogonal_basis - writing (see also 기저,basis#s-2)
Excerpts
정의 7.11: 직교 기저와 직교 정규 기저
즉
기저
나아가 기저를 이루는 모든 벡터의 길이가 1이면, // 길이,length 하나,one 단위,unit
즉
기저
(이승준 p145)
직교성,orthogonality 기저,basis
}
}
정규직교기저 orthonormal_basis - writing
표준기저,standard_basis - 기저 set 중에서 서로 모두 orthogonal and 길이가 모두 1 (normalized, unit) 인 특수한 경우? CHK
쌍대기저,dual_basis - writing
2022-09-25
power_basis
integral_basis - https://planetmath.org/integralbasis
/* 기타 basis 들은![[https]](/123/imgs/https.png) kms basis
kms basis ![[https]](/123/imgs/https.png) kms 기저 보고 추가 */
kms 기저 보고 추가 */
표준기저,standard_basis - 기저 set 중에서 서로 모두 orthogonal and 길이가 모두 1 (normalized, unit) 인 특수한 경우? CHK
쌍대기저,dual_basis - writing
2022-09-25
power_basis
integral_basis - https://planetmath.org/integralbasis
/* 기타 basis 들은
![[https]](/123/imgs/https.png) kms basis
kms basis ![[https]](/123/imgs/https.png) kms 기저 보고 추가 */
kms 기저 보고 추가 */CHK: 대략, 서로 선형독립,linear_independence인데 선형결합,linear_combination을 해서 벡터공간,vector_space을 만들 수 있는 ...그런데 필요 이상의 개수는 존재하지 않는? ... 벡터,vector들의 집합,set?
linearly independent한 (아마 유한개??) 것들이 (span해서 전체를 덮으면/전체로 span하면) 그것들이 바로 기저????(notsure)
(정확한 서술 필요)
벡터공간 V에 속한 선형독립,linear_independence인 벡터들의 최대 집합을 벡터공간 V의 기저라고 한다. 따라서, V에 속한 한 개 이상의 벡터를 기저에 첨가하면, 이 집합은 선형종속이 된다. 따라서, 기저에 속한 벡터의 개수는 dim V와 같다. (see 차원,dimension)
(Kreyszig)
(Kreyszig)
벡터공간,vector_space 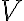 안의 벡터 집합
안의 벡터 집합 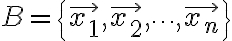 을 고려한다.
을 고려한다.
집합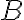 가 선형독립,linear_independence이고,
가 선형독립,linear_independence이고,
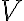 안의 모든 벡터가 이 벡터들의 선형결합,linear_combination으로 표현될 수 있다면,
안의 모든 벡터가 이 벡터들의 선형결합,linear_combination으로 표현될 수 있다면,
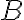 는
는 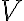 를 위한 기저(basis)라고 한다.
를 위한 기저(basis)라고 한다.
집합
(Zill Def 7.6.4 Basis for a Vector Space)
//차원과...
기저의 수와 차원은 밀접.
기저 안의 원소(벡터)의 수가 차원,dimension. <- 여기 예전 서술
V의 한 기저에 들어 있는 벡터의 개수가 차원이며 dim V로 나타냄. <- 저기 현재 서술
(이하 차원의 존재성과 유일성 간단히 언급)
}
기저의 수와 차원은 밀접.
기저 안의 원소(벡터)의 수가 차원,dimension. <- 여기 예전 서술
V의 한 기저에 들어 있는 벡터의 개수가 차원이며 dim V로 나타냄. <- 저기 현재 서술
(이하 차원의 존재성과 유일성 간단히 언급)
}
2. 정규/직교/정규직교 기저 ¶
정규기저,normal_basis
직교기저,orthogonal_basis
![[https]](/123/imgs/https.png) 수학백과: 직교기저
수학백과: 직교기저
https://mathworld.wolfram.com/OrthogonalBasis.html
 Orthogonal_basis
Orthogonal_basis
https://encyclopediaofmath.org/wiki/Orthogonal_basis
정규직교기저,orthonormal_basis
정규기저(normal basis) : 노름이 1, 노름,norm
직교기저(orthogonal basis) : 모두 서로 수직,
정규직교기저(orthonormal basis) : 정규직교이자 직교기저인 기저
 기저_(선형대수학)
기저_(선형대수학)
직교기저,orthogonal_basis
![[https]](/123/imgs/https.png) 수학백과: 직교기저
수학백과: 직교기저https://mathworld.wolfram.com/OrthogonalBasis.html
https://encyclopediaofmath.org/wiki/Orthogonal_basis
정규기저(normal basis) : 노름이 1, 노름,norm
직교기저(orthogonal basis) : 모두 서로 수직,
정규직교기저(orthonormal basis) : 정규직교이자 직교기저인 기저
항상 서로 수직이고 길이가 1
인 것 같다. CHK; from 정규직교기저는 그람-슈미트_과정,Gram-Schmidt_process 관련.
3. 순서기저 ordered basis ¶
기저들의 순서,order가 중요한 경우 이렇게??
순서집합,ordered_set의 일종?
tmp
{
https://chocobear.tistory.com/116 이 글에서 선형변환,linear_transformation의 행렬 표현을 알아보기 위해 순서기저를 먼저 정의
}
{
https://chocobear.tistory.com/116 이 글에서 선형변환,linear_transformation의 행렬 표현을 알아보기 위해 순서기저를 먼저 정의
}
4. 기저가 될 수 있는/없는 조건 ¶
상식적으로,
수식으로는
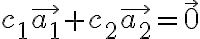
을 만족하는 ) 가 존재하면 기저벡터가 될 수 없다.
가 존재하면 기저벡터가 될 수 없다.
(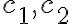 중 적어도 하나는 0이 아님 )
중 적어도 하나는 0이 아님 )
- 영벡터는 안된다.
- collinear하면 안된다.
수식으로는
(
이유는, 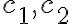 모두 0이 아니면
모두 0이 아니면
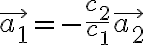
인데 이것은 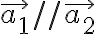 를 뜻하며 (위에서 collinear 조건)
를 뜻하며 (위에서 collinear 조건)
둘 중 하나가 0이고 다른 하나가 0이 아니면, 예를 들어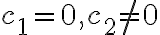 이면
이면 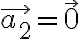 이렇게 영벡터가 되기 때문.
이렇게 영벡터가 되기 때문.
둘 중 하나가 0이고 다른 하나가 0이 아니면, 예를 들어
요소의 조합 중에 일차종속이 아닌 것은 일차독립.
(나카이 에츠지)
5. 기저벡터가 만드는 평행사변형 ¶
2D에서, 기저 벡터는 평행사변형을 만들며, 이 면적은
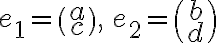
일 때
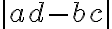
즉 (행렬식의 절대값) = (일차변환의 확대율)
// 확대율이란 e1=(1,0),e2=(0,1)가 만드는 1×1=1의 cell에 비해 e1',e2'가 만드는 cell의 크기(평행사변형의 면적)가 얼마나 되는지 얘기.
// 확대율이란 e1=(1,0),e2=(0,1)가 만드는 1×1=1의 cell에 비해 e1',e2'가 만드는 cell의 크기(평행사변형의 면적)가 얼마나 되는지 얘기.
(나카이 에츠지)
10. etc ¶
벡터공간이 있으면 기저를 항상 찾을 수 있다. (Zorn's lemma를 이용한다고)
한 벡터공간의 기저는 유일하지 않다. (기저 벡터 하나에 스칼라배를 해도 ok이므로)
한 벡터공간의 기저의 수는 유일하다.
기저 변환은 transition matrix 관련. (추이행렬,transition_matrix)
11. tmp links ko ¶
관련: (to link)
생성,span
차원,dimension .... 기저의 원소,element의 수, 즉 기저 속 벡터,vector의 수 - 이것이 차원? 100% 일치? chk
선형성,linearity
일차독립/일차종속 - see 선형독립,linear_independence
생성,span
차원,dimension .... 기저의 원소,element의 수, 즉 기저 속 벡터,vector의 수 - 이것이 차원? 100% 일치? chk
선형성,linearity
일차독립/일차종속 - see 선형독립,linear_independence
서로 다른 basis끼리는 independent하다. (you know.) 이것에 대해 독립과 관련지어 서술할 것. TBW
일차결합(선형결합,linear_combination)축,axis과 분명 관련있는데... 정확히?
기저를 기하학,geometry적으로 나타낸다면, 각 축 방향으로의 단위벡터,unit_vector들이 기저와 동등?
주성분분석,principal_component_analysis,PCA은 원 data의 분산,variance을 최대한 보존(?)하는 축을/기저를 찾으면서 차원축소 dimensionality_reduction 를 하는 것.
기저를 기하학,geometry적으로 나타낸다면, 각 축 방향으로의 단위벡터,unit_vector들이 기저와 동등?
주성분분석,principal_component_analysis,PCA은 원 data의 분산,variance을 최대한 보존(?)하는 축을/기저를 찾으면서 차원축소 dimensionality_reduction 를 하는 것.
수학적귀납법,mathematical_induction은 basis와 inductive_step s(귀납,induction적 단계,step들)로 이루어짐.
저 basis는 아마 기저로 번역될 건 아니고 base_case 와 동의어?
저 basis는 아마 기저로 번역될 건 아니고 base_case 와 동의어?
AKA 기저벡터 chk
Twins:
![[https]](/123/imgs/https.png) 수학백과: 기저
수학백과: 기저
![[https]](/123/imgs/https.png) 수학백과: 기저(위상수학) <- 위상,topology? chk
수학백과: 기저(위상수학) <- 위상,topology? chk
 Basis_(linear_algebra)
Basis_(linear_algebra)
 Basis_(linear_algebra)
Basis_(linear_algebra)
 기저_(선형대수학)
기저_(선형대수학)
https://mathworld.wolfram.com/Basis.html - 뜻이 많으므로 설명을 하지 않고,
https://mathworld.wolfram.com/VectorBasis.html - 여기서 설명함.
https://everything2.com/title/basis for a vector space
![[https]](/123/imgs/https.png) https://en.citizendium.org/wiki/Basis_(linear_algebra)
https://en.citizendium.org/wiki/Basis_(linear_algebra)
 기저
기저
![[https]](/123/imgs/https.png) 물리학백과: 기저
물리학백과: 기저
![[https]](/123/imgs/https.png) 수학백과: 기저
수학백과: 기저![[https]](/123/imgs/https.png) 수학백과: 기저(위상수학) <- 위상,topology? chk
수학백과: 기저(위상수학) <- 위상,topology? chkhttps://mathworld.wolfram.com/Basis.html - 뜻이 많으므로 설명을 하지 않고,
https://mathworld.wolfram.com/VectorBasis.html - 여기서 설명함.
https://everything2.com/title/basis for a vector space
![[https]](/123/imgs/https.png) https://en.citizendium.org/wiki/Basis_(linear_algebra)
https://en.citizendium.org/wiki/Basis_(linear_algebra)![[https]](/123/imgs/https.png) 물리학백과: 기저
물리학백과: 기저
