디랙 델타 함수 Dirac delta function AKA 델타 함수 delta function
다음 두 조건을 만족하는 함수이다.
 = \begin{cases} +\infty & (x = 0) \\ 0 & (x \ne 0) \end{cases})
 \, dx = 1)
단위임펄스함수,unit_impulse_function와 동일?
크로네커_델타,Kronecker_delta와 관련성 TBW
단위계단함수,unit_step_function과 차이 tbw
비약 불연속(jump discontinuity)의 개념 적절한 곳에 적을 것 tbw
{
이 점에서는 좌극한과 우극한이 둘 다 존재하나 서로 같지 않아서 결국 극한,limit이 존재하지 않는다. 그리고 불연속(불연속성,discontinuity)이다. chk
}
- wpen첫부분 "also known as the unit impulse"
임펄스함수,impulse_function크로네커_델타,Kronecker_delta와 관련성 TBW
단위계단함수,unit_step_function과 차이 tbw
비약 불연속(jump discontinuity)의 개념 적절한 곳에 적을 것 tbw
{
이 점에서는 좌극한과 우극한이 둘 다 존재하나 서로 같지 않아서 결국 극한,limit이 존재하지 않는다. 그리고 불연속(불연속성,discontinuity)이다. chk
}
적분하면 부호함수와 관련, chk 부호,sign
6. Excerpts ¶
정의 4.1: 델타 함수
) 가
가 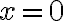 을 포함하는 임의의 유한한 구간에서 연속인 함수라고 할 때,
을 포함하는 임의의 유한한 구간에서 연속인 함수라고 할 때,
델타 함수) 는 다음 식으로 정의된다.
는 다음 식으로 정의된다.
 g(x) dx = g(0))
(중략)
델타 함수
정의에 따르면 사실 델타 함수는 일반적인 의미에서의 함수라고 볼 수는 없으며, 즉 임의의  에 대해 함수의 값이 유일하게 정의되지 않으므로, 정확하게 표현하면 델타 함수는 일반화된 함수(generalized function)에 속한다.
에 대해 함수의 값이 유일하게 정의되지 않으므로, 정확하게 표현하면 델타 함수는 일반화된 함수(generalized function)에 속한다.
(이승준 p77-80)
Twins:
 Dirac_delta_function
Dirac_delta_function
https://ghebook.blogspot.com/2011/10/dirac-delta-function.html
https://freshrimpsushi.github.io/posts/dirac-delta-function/
https://proofwiki.org/wiki/Definition:Dirac_Delta_Function
https://en.citizendium.org/wiki/Dirac_delta_function
![[https]](/123/imgs/https.png) 수학백과: 디랙 델타함수
수학백과: 디랙 델타함수
![[https]](/123/imgs/https.png) 물리학백과: 디랙 델타 함수
물리학백과: 디랙 델타 함수
![[https]](/123/imgs/https.png) 물리학백과: 델타함수
물리학백과: 델타함수
델타함수,delta_function
https://ghebook.blogspot.com/2011/10/dirac-delta-function.html
https://freshrimpsushi.github.io/posts/dirac-delta-function/
https://proofwiki.org/wiki/Definition:Dirac_Delta_Function
https://en.citizendium.org/wiki/Dirac_delta_function
![[https]](/123/imgs/https.png) 수학백과: 디랙 델타함수
수학백과: 디랙 델타함수![[https]](/123/imgs/https.png) 물리학백과: 디랙 델타 함수
물리학백과: 디랙 델타 함수![[https]](/123/imgs/https.png) 물리학백과: 델타함수
물리학백과: 델타함수델타함수,delta_function
https://everything2.com/title/Dirac delta function
http://en.citizendium.org/wiki/dirac_delta_function
 디랙_델타_함수
디랙_델타_함수
https://mathworld.wolfram.com/DeltaFunction.html
 디랙_델타_함수
디랙_델타_함수
http://en.citizendium.org/wiki/dirac_delta_function
https://mathworld.wolfram.com/DeltaFunction.html
----
- [1] Weisstein, Eric W. "Kronecker Delta." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/KroneckerDelta.html


![[http]](/123/imgs/http.png)