참이나 거짓 여부를 객관적으로 정할(판단할) 수 있는 문장.
참인지 거짓인지 판별할 수 있는 의미있는 평서문.
참인지 거짓인지를 명확하게 판별할 수 있는 문장,sentence이나 식,expression.[1]
의미론적으로semantically(semantics) 해석,interpretation되어 진리값,truth_value을 갖는 것으로 의도된(intended) 것? 현대 논리학에선 먼저 문맥 or 맥락(context)을 명시한 뒤에 그 안에서 명제를 고려하는 것이 깔끔하다(clean). (nlab)
참인지 거짓인지 판별할 수 있는 의미있는 평서문.
참인지 거짓인지를 명확하게 판별할 수 있는 문장,sentence이나 식,expression.[1]
의미론적으로semantically(semantics) 해석,interpretation되어 진리값,truth_value을 갖는 것으로 의도된(intended) 것? 현대 논리학에선 먼저 문맥 or 맥락(context)을 명시한 뒤에 그 안에서 명제를 고려하는 것이 깔끔하다(clean). (nlab)
따라서 두 가지로 분류 가능:
이 둘 이외에 다른 것은 없음(배중률,law_of_excluded_middle) - chk
할당한 것을 진리값,truth_value이라고 한다. (수백)
이 둘 이외에 다른 것은 없음(배중률,law_of_excluded_middle) - chk
QQQ 배중률을 인정하지 않는 (고전논리학이 아닌) 그런 체계에서는 이 문단은 의미가 없는건지? - chk.
고전논리학에서할당한 것을 진리값,truth_value이라고 한다. (수백)
관행적 기호: p, q, r, …
명제가
명제가
p이면 q이다즉
꼴일 때, p를 가정, q를 결론이라고 한다.
Sub:
{
conditional propositions 조건명제
조건명제,conditional_proposition
등치명제,biconditional_proposition
단순명제,simple_proposition simple proposition = primary proposition = atomic proposition ?
 합성명제 복합명제
합성명제 복합명제  합성명제 복합명제
합성명제 복합명제
(쌍방)조건명제 biconditional
추측,conjecture
명제식: 일상어가 아닌 논리기호로 써서 애매하지 않은 명제?
명제논리,propositional_logic
명제함수,propositional_function - 작성중
명제변수,propositional_variable - 작성중
propositional_formula 명제식? - 작성중
propositional_calculus (kms: 명제계산법[2]) -> (curr at 형식체계,formal_system) 명제논리,propositional_logic 및 영차논리,zeroth-order_logic와 동의어. chk
propositional_connective 명제연결사?
 Premise앞부분 참조.
Premise앞부분 참조.  premise
premise
chk:
원자명제 : 더 작은 명제로 표현할 수 없는 명제 atomic_proposition ... 더 이상 쪼갤 수 없는 명제. 명제논리,propositional_logic는 원자명제에 유한한 논리연산을 가하여 구성할 수 있는 명제들을 다루는 논리체계(형식체계,formal_system).
합성명제 : 더 작은 명제로 표현할 수 있는 명제 compound_proposition
chk
{
단순명제: 한 가지 사실을 주장하는 명제
합성명제: 연결사를 써서 단순명제를 이어 만든 명제
}
## from 황병연 http://www.kocw.net/home/search/kemView.do?kemId=1395260 논리와명제1 12:30
단순명제simple_proposition: 하나의 문장,statement이나 식,expression으로 구성한 명제
합성명제composition proposition: 여러 단순 명제들이 논리연산자(들)로 연결해 만든 명제
'장미꽃은 빨갛다', '유채꽃은 노랗다' : 단순명제
'장미꽃은 빨갛고 유채꽃은 노랗다' : 합성명제
선언명제 : disjunctive proposition : 2개의 명제가 선언(選言)의 기호 '∨'로 결부된 것.
chk; tmp from https://m.blog.naver.com/hafs_snu/221094765804chk: 한 문장이나 식으로 구성
합성명제가 아닌 명제
= 원자명제 atomic_proposition ? chk simple.proposition vs atomic.proposition
simple.proposition vs atomic.proposition
합성명제,compound_proposition =복합명제? ... 합성명제가 아닌 명제
= 원자명제 atomic_proposition ? chk
chk: 여러 단순명제들이 논리연산자 또는 연결사(logical_operator or connective = 연결사,connective = 논리연결사,logical_connective)로 연결되어 만들어진 명제,proposition.
단순명제에 비해 진리값을 알아내기 복잡하므로 진리표,truth_table를 사용하여 단계적으로 알아내면 편리하다.
compound proposition
단순명제들을 (논리연산자,logical_operators or 연결사connectives)로 연결해 합성명제를 만들 수 있다.
![[https]](/123/imgs/https.png) 수학백과: 합성명제(easy)
수학백과: 합성명제(easy)
항진명제,tautology - 항상 참이 되는 명제단순명제에 비해 진리값을 알아내기 복잡하므로 진리표,truth_table를 사용하여 단계적으로 알아내면 편리하다.
compound proposition
단순명제들을 (논리연산자,logical_operators or 연결사connectives)로 연결해 합성명제를 만들 수 있다.
![[https]](/123/imgs/https.png) 수학백과: 합성명제(easy)
수학백과: 합성명제(easy)chk: 진리값,truth_value이 항상 참인 명제
동일률 p→p, 배중률 p∨(~p)
ex. "C는 까마귀이다 또는 C는 까마귀가 아니다"
![[https]](/123/imgs/https.png) 수학의 세계: 항진명제와 동치명제
수학의 세계: 항진명제와 동치명제
항상 참인 명제. '참인 명제'와는 의미가 다름.
비슷: 항진식
반대: 모순명제=항위명제 contradiction
![[https]](/123/imgs/https.png) 수학백과: 항진명제
수학백과: 항진명제
항진명제 : 논리식이나 합성명제에서, 각 명제의 모든 참/거짓 조합에 대해, 항상 참인 것. from http://www.aistudy.com/logic/tautology.htm
항진=tautology: curr at 논리학,logic#s-6.1
논리학,logic#s-6.1
Sub
Twin
https://everything2.com/title/tautology
https://encyclopediaofmath.org/wiki/Tautology
Up: 명제,proposition
모순명제 = 항위명제 : 모순,contradiction동일률 p→p, 배중률 p∨(~p)
ex. "C는 까마귀이다 또는 C는 까마귀가 아니다"
![[https]](/123/imgs/https.png) 수학의 세계: 항진명제와 동치명제
수학의 세계: 항진명제와 동치명제항상 참인 명제. '참인 명제'와는 의미가 다름.
비슷: 항진식
반대: 모순명제=항위명제 contradiction
![[https]](/123/imgs/https.png) 수학백과: 항진명제
수학백과: 항진명제항진명제 : 논리식이나 합성명제에서, 각 명제의 모든 참/거짓 조합에 대해, 항상 참인 것. from http://www.aistudy.com/logic/tautology.htm
항진=tautology: curr at
Sub
Twin
https://everything2.com/title/tautology
https://encyclopediaofmath.org/wiki/Tautology
Up: 명제,proposition
(쌍방)조건명제 biconditional
추측,conjecture
명제식: 일상어가 아닌 논리기호로 써서 애매하지 않은 명제?
명제논리,propositional_logic
명제함수,propositional_function - 작성중
명제변수,propositional_variable - 작성중
propositional_formula 명제식? - 작성중
propositional_calculus (kms: 명제계산법[2]) -> (curr at 형식체계,formal_system) 명제논리,propositional_logic 및 영차논리,zeroth-order_logic와 동의어. chk
propositional_connective 명제연결사?
https://encyclopediaofmath.org/wiki/Propositional_connective
ex. conjunction disjunction implication negation equivalence Sheffer_stroke
전제,premise is_a proposition. 관계는 ex. conjunction disjunction implication negation equivalence Sheffer_stroke
chk:
원자명제 : 더 작은 명제로 표현할 수 없는 명제 atomic_proposition ... 더 이상 쪼갤 수 없는 명제. 명제논리,propositional_logic는 원자명제에 유한한 논리연산을 가하여 구성할 수 있는 명제들을 다루는 논리체계(형식체계,formal_system).
합성명제 : 더 작은 명제로 표현할 수 있는 명제 compound_proposition
chk
{
단순명제: 한 가지 사실을 주장하는 명제
합성명제: 연결사를 써서 단순명제를 이어 만든 명제
}
## from 황병연 http://www.kocw.net/home/search/kemView.do?kemId=1395260 논리와명제1 12:30
단순명제simple_proposition: 하나의 문장,statement이나 식,expression으로 구성한 명제
합성명제composition proposition: 여러 단순 명제들이 논리연산자(들)로 연결해 만든 명제
1. composite/composed가 아니고? 위에는 또 compound라고 썼는데 2. 복합명제도 되나? 아님 다른뜻?
ex.'장미꽃은 빨갛다', '유채꽃은 노랗다' : 단순명제
'장미꽃은 빨갛고 유채꽃은 노랗다' : 합성명제
선언명제 : disjunctive proposition : 2개의 명제가 선언(選言)의 기호 '∨'로 결부된 것.
원리적으로는 2개의 조합기호가 충분하나, 보통 다음 4개의 기호가 쓰인다.
연언(連言: ∧), 선언(選言: ∨), 함의(含意: ⊃), 부정(否定: ∼)
from![[https]](/123/imgs/https.png) 두산백과: 선언명제
두산백과: 선언명제
연언(連言: ∧), 선언(選言: ∨), 함의(含意: ⊃), 부정(否定: ∼)
from
![[https]](/123/imgs/https.png) 두산백과: 선언명제
두산백과: 선언명제{
conditional propositions 조건명제
조건명제,conditional_proposition
p→q
if p then q
다른 말로if p then q
q, if p
p only if q - 구어체와 용법이 다르다고
when p, q
p는 가정,hypothesis, q는 결론,conclusion
p가 될 필요조건,necessary_condition은 q
a necessary condition for p is q
q가 될 (q에 필요한??) 충분조건,sufficient_condition은 p
a sufficient condition for q is p
biconditional proposition 등치명제p only if q - 구어체와 용법이 다르다고
when p, q
p는 가정,hypothesis, q는 결론,conclusion
p가 될 필요조건,necessary_condition은 q
a necessary condition for p is q
q가 될 (q에 필요한??) 충분조건,sufficient_condition은 p
a sufficient condition for q is p
등치명제,biconditional_proposition
p↔q
p iff q
p if and only if q
(p→q)∧(q→p)와 완전히 동일
}p iff q
p if and only if q
(p→q)∧(q→p)와 완전히 동일
맛있는해석학 p13에서.
| 명제 이름 | 명제 | |
| 전칭명제 | ∀x, p(x) | ∀는 전칭기호 |
| 존재명제 | ∃x, p(x) | ∃는 존재기호 |
| 한정명제 | 전칭명제와 존재명제를 통틀어 한정명제라 부름 | ∀, ∃를 통틀어 한정기호라 부름 |
Related:
진리값,truth_value : 어떤 명제의 내용이 참인지 거짓인지를 나타내는 값. 따라서 당연히 참,true 또는 거짓,false. - curr chkout 진리표,truth_table bottom
괴델_수,Goedel_number
괴델_수,Goedel_number
단순명제와 복합명제
복합명제 검토에 진리표,truth_table가 쓰임.
부정(~), 연결기호(∧, ∨), ⇒를 써서 단순명제로부터 복합명제를 생성할 수 있다.
conjunction 논리곱
disjunction 논리합
conditional proposition 조건명제
biconditional proposition 등치명제![[https]](/123/imgs/https.png) CHK
CHK
tautology 항진명제
disjunction 논리합
conditional proposition 조건명제
biconditional proposition 등치명제
![[https]](/123/imgs/https.png) CHK
CHKtautology 항진명제
...에서 몇개를 표로 나타내면....
| 표기 | in human language | |
| 논리곱 conjunction | p∧q | p and q |
| 논리합 disjunction | p∨q | p or q |
| 조건명제 conditional prop. | p→q | if p then q q, if p p only if q(이거 순서 맞나??? CHK) when p, q (여기서 p는 가정hypothesis이고 q는 결론conclusion) |
| equivalence? | p≡q | ? |
| 등치명제 biconditional prop. | p↔q | p if and only if q |
연산자우선순위 or 연산순서 는
명시된 괄호
¬ not
∧ and
∨ or
→ then
인듯? 항상?¬ not
∧ and
∨ or
→ then
(고딩, easy) p→q형태의 명제 얘기들, CLEANUP, del ok ¶
명제 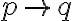 가 참이면
가 참이면 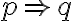 로 표기.
로 표기.
명제 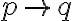 의
의
명제가 거짓이면 그 대우명제도 거짓
- 역 :
- 이 :
- 대우 :
명제가 거짓이면 그 대우명제도 거짓
술어와의 비교 ¶
명제와 술어,predicate 비교 TBW
{ 내 생각 대충임, chk
ex.
1+1=2는 명제이다.
1+x=2는 술어이다.
1+1=2는 참인 명제이다.
1+x=2는 x가 정해지지 않은 경우 명제라고 할 수 없다.
}
{ 내 생각 대충임, chk
ex.
1+1=2는 명제이다.
1+x=2는 술어이다.
변수,variable x의 값이 1일 때 이 술어는 참인 명제가 되고, (컴퓨터 식,expression으로 표현된 경우 x에 1이 대입,assignment되면)
변수,variable x의 값이 1이 아닌 다른 값일 때 이 술어는 거짓인 명제가 된다.
1+1=1은 거짓인 명제이다.변수,variable x의 값이 1이 아닌 다른 값일 때 이 술어는 거짓인 명제가 된다.
1+1=2는 참인 명제이다.
1+x=2는 x가 정해지지 않은 경우 명제라고 할 수 없다.
}
현재는 see 술어논리,predicate_logic - 저기 약간의 내용 있음
명제와 정리 ¶
참인 명제들 중에서 중요한 것들을 정리,theorem라고 한다.
다른 명제를 증명하기 위해 유용한 예비 명제(preliminary proposition)를 보조정리,lemma라고 한다.
정리에서 조금 더 나아간 것을 따름정리,corollary라고 한다.
이 구분은 명확한 것은 아니다.
(mcs.pdf 1.3)
다른 명제를 증명하기 위해 유용한 예비 명제(preliminary proposition)를 보조정리,lemma라고 한다.
정리에서 조금 더 나아간 것을 따름정리,corollary라고 한다.
이 구분은 명확한 것은 아니다.
(mcs.pdf 1.3)
See also ¶
이산수학,discrete_math - 관련 단어/표현(영어).
불_대수,Boolean_algebra
논리,logic
불_논리,Boolean_logic or 이진논리 : 명제는 T or F 2가지의 진리값만을 가지므로 이진논리라고 함.
수리논리,mathematical_logic
조건,condition
증명,proof
 명제proposition
명제proposition
불_대수,Boolean_algebra
논리,logic
불_논리,Boolean_logic or 이진논리 : 명제는 T or F 2가지의 진리값만을 가지므로 이진논리라고 함.
수리논리,mathematical_logic
조건,condition
증명,proof
chk: 명제를 참,true인지 거짓,false인지 판단하는 과정이 증명?
Q: 진술,statement과 proposition의 차이?iff는 아님 결과가 두가지인 경우만이 증명이 아니고 과정을 명쾌하게 보이면 증명이니까, 다만 증명의 일종?
밑에 수학백과: 명제에선 mathematical statement라는 단어 씀
mv from Twins:
https://foldoc.org/proposition
https://everything2.com/title/proposition
![[https]](/123/imgs/https.png) 수학백과: 명제
수학백과: 명제
https://encyclopediaofmath.org/wiki/Proposition
 Proposition
Proposition
 명제
명제
 Proposition
Proposition
https://ncatlab.org/nlab/show/proposition
https://foldoc.org/proposition
https://everything2.com/title/proposition
![[https]](/123/imgs/https.png) 수학백과: 명제
수학백과: 명제https://encyclopediaofmath.org/wiki/Proposition
https://ncatlab.org/nlab/show/proposition

