무한급수(간단히 급수로 줄여 부르기도 함. See 급수,series)
정의:
Sub:
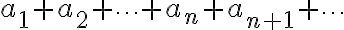
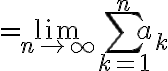
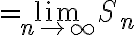
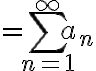

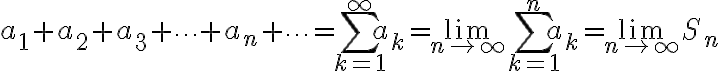
Sub:
무한등비급수 = 무한기하급수 → 기하급수,geometric_series 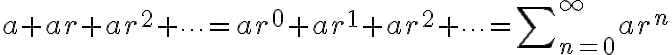
조화급수,harmonic_series
테일러_급수,Taylor_series
매클로린_급수,Maclaurin_series
멱급수,power_series
표기는 다양할 수 밖에.조화급수,harmonic_series
테일러_급수,Taylor_series
매클로린_급수,Maclaurin_series
멱급수,power_series
tmp ¶
무한 번 더해도 유한일 수 있다. 고대(그리스)에는 이것을 몰라서 (아님 알고도 논쟁을 만들기 위해?) 제논의 역설(Zeno's paradox)이란 게 있었다. - 역설,paradox
무한대,infinity 개념이 확립되지 않아서? CHK
예시는 무한급수 및 정적분,definite_integral등에서 숱하게 많으므로 생략
무한대,infinity 개념이 확립되지 않아서? CHK
예시는 무한급수 및 정적분,definite_integral등에서 숱하게 많으므로 생략
tmp; chk ¶
Memorize:
(각각 p급수,p-series, 무한기하급수,geometric_series)
from http://www.kocw.net/home/search/kemView.do?kemId=1141060 김도형 2. 14m
from http://www.kocw.net/home/search/kemView.do?kemId=1141060 김도형 2. 14m
tmp ¶
주의. ex.
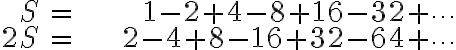
둘을 더하면
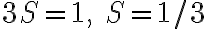 : clearly wrong
: clearly wrong
Bmks:
https://ghebook.blogspot.com/2010/10/infinite-series.html
https://ghebook.blogspot.com/2020/07/algebra-of-infinite-series.html
https://ghebook.blogspot.com/2010/10/infinite-series.html
https://ghebook.blogspot.com/2020/07/algebra-of-infinite-series.html

