Sub:
{
// TODO mv from 전미분,total_differential and
전미분,total_differential and  전미분,total_derivative
전미분,total_derivative
}
{
// TODO mv from
}
Contents
1. Definition ¶
The differential
Note: 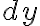 is a dependent variable; it depends on
is a dependent variable; it depends on 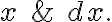
2. Definition (Thomas) ¶
Let ) be a differentiable function.
be a differentiable function.
The differential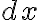 is an independent variable.
is an independent variable.
The differential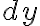 is
is
dx.)
The differential
The differential
: 독립변수,independent_variable
: 항상
와
에 의해 결정되는 종속변수,dependent_variable
즉,의 값이 주어지면
의 정의역,domain 내의
값에 의해
값이 결정됨.
는 자주
의 변화량
로 선택됨.
4. Definition (utk.edu) ¶
Definition. Let ) be a differentiable function.
be a differentiable function.
The differential of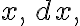 is an independent variable.
is an independent variable.
The differential of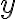 is defined as
is defined as
 dx)
(![[http]](/123/imgs/http.png) http://archives.math.utk.edu/visual.calculus/3/differentials.2/index.html)
http://archives.math.utk.edu/visual.calculus/3/differentials.2/index.html)
The differential of
The differential of
![[http]](/123/imgs/http.png) http://archives.math.utk.edu/visual.calculus/3/differentials.2/index.html)
http://archives.math.utk.edu/visual.calculus/3/differentials.2/index.html)5. Definition (Varberg) ¶
Definition
Let ) be a differentiable function of the independent variable
be a differentiable function of the independent variable 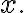
| Derivative Rule | Differential Rule |
7. Examples (misc) ¶
여기서
// http://kocw.net/home/search/kemView.do?kemId=1215229 이종광 20m
// from 차동우; https://youtu.be/IAIADoy83as?t=246
8. 미소~, ~ 미분소, differential length/area/volume/etc. ¶
기초 calculus에서 중적분(multiple integral)이 나올 때 쓰는 기호는
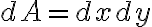
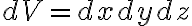
라 하고
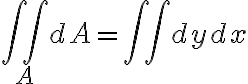
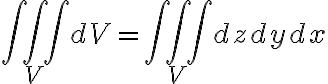
등을 보통 씀. Fubini's theorem에 의해 dx dy dz의 순서를 크게 신경쓰지 않아도 됨.
좌표계,coordinate_system에 따라 달라짐.
미소~ (ex. 미소변위)
~ 미분소 (ex.
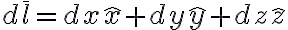
극좌표계, 원통좌표계의 미소면적/미소부피는 극좌표계,polar_coordinate_system 참조
~ 미분소 (ex.
선 미분소(differential line), 면적 미분소(differential area), 부피 미분소(differential volume) [1]
체적 미분소(differential volume)) , 면적 미분소(differential surface)
, 면적 미분소(differential surface) 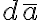 [2]
[2]
길이 미분소(length differential) [3])
선미분소 : 방향을 가진 매우 작은 선분의 극한 [4]체적 미분소(differential volume)
길이 미분소(length differential) [3])
(Ulaby: CHK, CLEANUP 특히 r, R을 각각 rho, r로 잘 바꾸었는지 check)
(rectangular coord system)
differential surface area: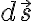
differential length: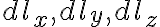
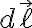
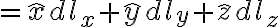
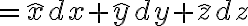
differential area in the
differential surface area:
differential length:
y-z plane: 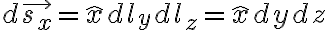
x-z plane:
x-y plane: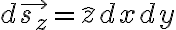
x-z plane:
x-y plane:
(cyl. coord system)
differential volume elements...........?
differential lengths along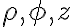 :
:
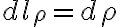
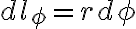
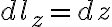
differential length:
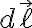
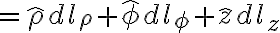

differential surface area:
 (φ-z cylindrical surface),
(φ-z cylindrical surface),
 (ρ-z plane),
(ρ-z plane),
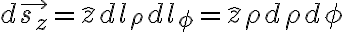 (ρ-φ plane).
(ρ-φ plane).
differential volume:
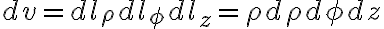
이상 완벽하게 r->rho 바꾸었는지 모르겠음
differential volume elements...........?
differential lengths along
(sph. coordinate system)
differential length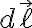

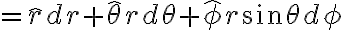
vector differential surface 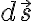
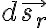
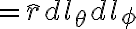
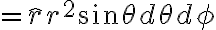 (θ-φ spherical surface),
(θ-φ spherical surface),
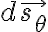
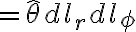
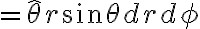 (r-φ conical surface),
(r-φ conical surface),
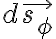
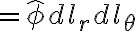
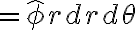 (r-θ plane)
(r-θ plane)
differential volume 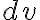
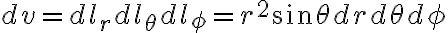
(이상 완벽하게 R->r 바꾸었는지 chk)
differential length
(이상 Ulaby 5e, 틀린지 chk)
이하
11. Calculus Made Easy №15(장?) ¶
따라서
이어서 탄젠트,tangent, 이계미분 나오는데 생략.
13. 기타 ¶
Sub:
{
https://en.wikipedia.org/wiki/Exact_differential
완전미분이 없으면 불완전미분(inexact differential)
 완전미분exact_differential
완전미분exact_differential
}
완전미분방정식exact de
미분형식,differential_form
{
https://en.wikipedia.org/wiki/Exact_differential
완전미분이 없으면 불완전미분(inexact differential)
}
완전미분방정식exact de
미분형식,differential_form
선형근사,linear_approximation와 밀접한데 관계 적을 것 TBW
AKA 미분소(素), 디퍼렌셜
Compare:
Sub:
미분,derivative (도함수)
미분,differentiation (도함수를 찾는 것)
무한소,infinitesimal - 비슷?
차분(difference) - see 차이,difference
Up:미분,differentiation (도함수를 찾는 것)
무한소,infinitesimal - 비슷?
차분(difference) - see 차이,difference
Sub:
미분방정식,differential_equation
미분연산자,differentiation_operator (curr at RR 미분연산자,differentiation_operator )
전미분,total_differential
Kaehler_differential =,Kaehler_differential . Kaehler_differential <- German umlaut transliteration을 찾아보면 (ä → ae)라서 pagename 이렇게 해야 할 듯 한데, chk
See also 디퍼렌셜예제가있는페이지미분연산자,differentiation_operator (curr at RR 미분연산자,differentiation_operator )
전미분,total_differential
Kaehler_differential =,Kaehler_differential . Kaehler_differential <- German umlaut transliteration을 찾아보면 (ä → ae)라서 pagename 이렇게 해야 할 듯 한데, chk
{
Kähler differential
https://ko.wikipedia.org/wiki/켈러_미분
https://en.wikipedia.org/wiki/Kähler_differential
https://ja.wikipedia.org/wiki/ケーラー微分
https://ncatlab.org/nlab/show/Kähler differential
...
"Kähler differential"
 Kähler differential
Kähler differential
 Kähler differential
Kähler differential
}
Kähler differential
https://ko.wikipedia.org/wiki/켈러_미분
https://en.wikipedia.org/wiki/Kähler_differential
https://ja.wikipedia.org/wiki/ケーラー微分
https://ncatlab.org/nlab/show/Kähler differential
...
"Kähler differential"
}
Related: Compare: 차이,difference(=차분)


![[https]](/123/imgs/https.png)