베이즈 정리 Bayes' theorem, AKA 베이즈 법칙 Bayes' rule
1. ? ¶
보통 P(B|A)에서 P(A|B)로 갈 때 쓰이나? CHK
결과 관측에서 원인을 추론할 때 유용?
결과 관측에서 원인을 추론할 때 유용?
// tmp from 마스터 알고리즘 책
P(원인|결과) = P(원인) × P(결과|원인) / P(결과)
P(원인|결과) = P(원인) × P(결과|원인) / P(결과)
ex. 지난달 100명 환자, 14명 독감 걸렸고, 20명은 열이 있었고, 11명은 독감에 걸리고 열도 있었다.
독감이 걸렸을 때 열이 나는 조건부 확률 = 11/14 // 조건부확률,conditional_probability
모든 환자 중 열이 나는 확률 = 20/100
독감 걸린 환자 중 열이 있는 확률 = 11/14
독감 and 열이 나는 확률 = P(독감, 발열) = P(독감) × P(발열|독감) = 14/100 × 11/14 = 11/100
이 값을 다른 방식으로 구할 수 있다.
P(독감, 발열) = P(발열) × P(독감|발열) // 조건부확률의 정의에 따라
// 그런데 위의 P(독감, 발열)과 식이 같다. 그걸 가져와서 쓰면
P(발열) × P(독감|발열) = P(독감) × P(발열|독감)
양변을 P(발열) 로 나누면
P(독감|발열) = P(독감) × P(발열|독감) / P(발열)
// 이걸 계산하면, 14/100 × 11/14 ÷ 20/100 = 11/20
독감이 걸렸을 때 열이 나는 조건부 확률 = 11/14 // 조건부확률,conditional_probability
모든 환자 중 열이 나는 확률 = 20/100
독감 걸린 환자 중 열이 있는 확률 = 11/14
독감 and 열이 나는 확률 = P(독감, 발열) = P(독감) × P(발열|독감) = 14/100 × 11/14 = 11/100
이 값을 다른 방식으로 구할 수 있다.
P(독감, 발열) = P(발열) × P(독감|발열) // 조건부확률의 정의에 따라
// 그런데 위의 P(독감, 발열)과 식이 같다. 그걸 가져와서 쓰면
P(발열) × P(독감|발열) = P(독감) × P(발열|독감)
양변을 P(발열) 로 나누면
P(독감|발열) = P(독감) × P(발열|독감) / P(발열)
// 이걸 계산하면, 14/100 × 11/14 ÷ 20/100 = 11/20
조건부확률의 정의에 따라
=\frac{P(A\cap B)}{P(B)})
=\frac{P(A\cap B)}{P(A)})
위 두 식에 따라,
P(B)=P(A\cap B)=P(B|A)P(A))
이다. (같은 내용 조건부확률,conditional_probability 페이지에도 있음)
여기에서 베이즈 법칙(Bayes' rule)의 가장 기본적인 형태를 얻는다.
=\frac{P(B|A)P(A)}{P(B)})
(Schaum's outline)
여기에서 베이즈 법칙(Bayes' rule)의 가장 기본적인 형태를 얻는다.
Bayes' Theorem or Rule
그것들의 합집합,union이 표본공간,sample_space
그렇다면 임의의 사건
이 때문에 베이즈 정리는 가끔 theorem on the probability of causes라고도 불린다.
(Schaum Prob and Stat p9)
두 가지 꼴: 간단한 형태, 일반적인 형태
....
CHK
CHK
2. Cor. ¶
조건부확률,conditional_probability 관련. 두 사건,event A, B에 대해 P(B|A)에서 P(A|B)로 갈 수 있게 해 준다. 두 사건과 두 결과,outcome(A and Ac)의 경우만 보면,
=\frac{P(B|A)P(A)}{P(B|A)P(A)+P(B|A^c)P(A^c)})
3. 정리 ¶
TOCLEANUP
A1, ..., An: partition of S with P(Ai)>0
P(Ai|B)
= P(Ai ∩ B) / P(B)
= {P(Ai)P(B|Ai)} / {P(A1)P(B|A1) + ... + P(An)P(B|An)}
= {P(Ai)P(B|Ai)} / {P(A1)P(B|A1) + ... + P(An)P(B|An)}
이 식의 의미는 사건 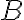 가 일어난 조건 하에서 사건
가 일어난 조건 하에서 사건 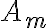 이 일어날 확률을 구하는 데 있어, 역조건확률, 즉 사건
이 일어날 확률을 구하는 데 있어, 역조건확률, 즉 사건 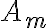 이 일어난 조건하의 사건
이 일어난 조건하의 사건 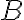 의 확률들을 사용하여 표현할 수 있다는 것.
의 확률들을 사용하여 표현할 수 있다는 것.
B1, B2, …, Bn을 표본 공간 S의 분할,partition이라고 하자. 사건 A가 발생했다고 가정할 때 사건 Bj가 일어날 확률은?
조건부확률,conditional_probability의 정의에서 다음 식을 얻을 수 있다.
조건부확률,conditional_probability의 정의에서 다음 식을 얻을 수 있다.
(Leon-Garcia p.65)
서로 배반인(exclusive)  개의 사건,event
개의 사건,event 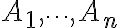 이
이
=1) 을 만족할 때,
을 만족할 때,
어떤 사건 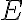 가 일어났다는 가정에서의 조건부확률,conditional_probability
가 일어났다는 가정에서의 조건부확률,conditional_probability ) 에 관한 정리
에 관한 정리
=\frac{P(E|A_i)P(A_i)}{\sum_{j=1}^{n}P(E|A_j)P(A_j)})
(![[https]](/123/imgs/https.png) from)
from)
![[https]](/123/imgs/https.png) from)
from)두 조건부확률 ) 와
와 ) 의 관계를 설명해 줌.
의 관계를 설명해 줌.
4. 사전확률/사후확률/가능도가 포함된 설명 ¶
Bayes formula
사건 A가 일어날 때, (일어났을 때?) 사건 B의 조건부확률,conditional_probability
=\frac{P(B\cap A)}{P(A)}=\frac{P(A|B)P(B)}{P(A|B)P(B)+P(A|B^c)P(B^c)})
사건 A가 일어날 때, (일어났을 때?) 서로 배반,disjoint인 사건들 ) 에 대한 확률
에 대한 확률
=\frac{P(A|B_j)P(B_j)}{\sum_1^n P(A|B_j) P(B_j)})
즉,
\propto P(A|B_j)P(B_j))
이것의 뜻은, A가 일어난 경우, 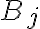 가 일어날 확률은
가 일어날 확률은 ) 와
와 ) 의 곱에 비례한다는 것.
의 곱에 비례한다는 것.
사건 A가 일어날 때, (일어났을 때?) 사건 B의 조건부확률,conditional_probability
: 사후확률 posterior
: 가능도,likelihood
: 사전확률 prior
tmp from ![[https]](/123/imgs/https.png) namu 나이브베이지안 2.1; chk
namu 나이브베이지안 2.1; chk
{
두 사건 A, B에 대해 베이즈 정리는
=\frac{P(B|A)P(A)}{P(B)})
여기서
) : 사전확률 prior probability - 원래부터 알고 있던 값
: 사전확률 prior probability - 원래부터 알고 있던 값
) :
: 사후확률 posterior probability
) : 사후확률 posterior probability (2022-02-12 에 보니까 고쳐져있네)
: 사후확률 posterior probability (2022-02-12 에 보니까 고쳐져있네)
베이즈 정리는 사전확률을 가지고 사후확률을 예측하거나 추론하는 데 쓸 수 있다는 의의가 있다.
![[https]](/123/imgs/https.png) namu 나이브베이지안 2.1; chk
namu 나이브베이지안 2.1; chk{
두 사건 A, B에 대해 베이즈 정리는
사건이 n개라면,
=P(A|B_1\cap B_2\cap \cdots \cap B_n)=\frac{P(B_1\cap B_2\cap\cdots\cap B_n|A)P(A)}{P(B)})
(여러 개의 사건으로 구성된다 = 교집합)인 이유? QQQ
이 때 나이브 베이지안 알고리듬은 순진한, 즉, B를 구성하는 모든 사건들이 서로 독립사건이라는 가정을 한다. 이렇게 하면 우변이 계산이 쉬운 형태로 변한다.
=\frac{P(B_1|A)P(B_2|A)\cdots P(B_n|A)P(A)}{P(B)})
우리가 알고 있는 것은 ) 뿐, 나머지는 문제 상황에 따라 적절하게 결정해야 함.
뿐, 나머지는 문제 상황에 따라 적절하게 결정해야 함.
대표적 방법: 가능한 선택지 중에서 가장 높은) 를 주는
를 주는 ) 들을 찾는 사후확률최대화 maximum a posteriori 방법 //
들을 찾는 사후확률최대화 maximum a posteriori 방법 // maximum.a.posteriori
maximum.a.posteriori
간단한 예를 들면,
) 가 모두 표준편차,standard_deviation
가 모두 표준편차,standard_deviation 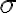 를 갖는 정규분포함수(see 정규분포,normal_distribution)
를 갖는 정규분포함수(see 정규분포,normal_distribution) ) 라고 가정하고,
라고 가정하고,
적절한 최적화,optimization방법을 동원해,
) 를 최대화,maximization시키는 정규분포함수의 평균
를 최대화,maximization시키는 정규분포함수의 평균 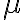 를 찾는 것이다.
를 찾는 것이다.
최적화문제를 풀 때 분모의) 는 결과에 영향을 미치지 않으므로
는 결과에 영향을 미치지 않으므로
이 때 나이브 베이지안 알고리듬은 순진한, 즉, B를 구성하는 모든 사건들이 서로 독립사건이라는 가정을 한다. 이렇게 하면 우변이 계산이 쉬운 형태로 변한다.
대표적 방법: 가능한 선택지 중에서 가장 높은
간단한 예를 들면,
적절한 최적화,optimization방법을 동원해,
최적화문제를 풀 때 분모의
- 생략하거나
- 상수
로 표현해두고 푸는 경우가 대부분이다.
5. 예제 ¶
3대의 기계 M1 M2 M3
각각 전 제품의 20%, 30%, 50% 생산
각 기계의 생산 불량률: 1%, 2%, 3%
무작위로 뽑은 하나의 제품이 불량이었다면, 이 불량품이 M2에서 생산되었을 확률은?
각각 전 제품의 20%, 30%, 50% 생산
각 기계의 생산 불량률: 1%, 2%, 3%
무작위로 뽑은 하나의 제품이 불량이었다면, 이 불량품이 M2에서 생산되었을 확률은?
sol.
S: 표본공간
B: 제품이 불량품일 사건
Ai: 제품이 Mi에 의하여 생산된 사건
S: 표본공간
B: 제품이 불량품일 사건
Ai: 제품이 Mi에 의하여 생산된 사건
제품이 Mi에 의하여 생산되었을 확률
=\frac{P(A_2)P(B|A_2)}{\textstyle\sum_{k=1}^3 P(A_k)P(B|A_k)})
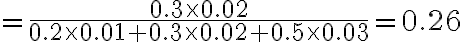
(from http://www.kocw.net/home/search/kemView.do?kemId=1162312 베이즈 정리)
P(A1)=0.2
P(A2)=0.3
P(A3)=0.5
기계 Mi에 의해 생산된 한 제품이 불량일 확률P(A2)=0.3
P(A3)=0.5
P(B|A1)=0.01
P(B|A2)=0.02
P(B|A3)=0.03
베이즈 정리에 의해P(B|A2)=0.02
P(B|A3)=0.03
8. Bayesian network ¶
belief_network, causal_network 도 같은 의미라고. (aistudy)
Bayes_network, decision_network 도 같음. (wpen)
Bayes_network, decision_network 도 같음. (wpen)
DAG = directed_acyclic_graph = directed acyclic 그래프,graph임
9. 나이브 베이지안, naive Bayesian ¶
tmp from ![[https]](/123/imgs/https.png) namu 나이브 베이지안 알고리즘
namu 나이브 베이지안 알고리즘
{
베이즈_정리,Bayes_theorem를 이용한 확률적 기계학습,machine_learning 알고리듬. 사전확률을 기반으로 사후확률을 추론하는 확률적 예측을 할 때, 모든 사건이 독립이라는 순진한(naive) 가정을 하고 있기 때문에, hence the name.
![[https]](/123/imgs/https.png) namu 나이브 베이지안 알고리즘
namu 나이브 베이지안 알고리즘{
베이즈_정리,Bayes_theorem를 이용한 확률적 기계학습,machine_learning 알고리듬. 사전확률을 기반으로 사후확률을 추론하는 확률적 예측을 할 때, 모든 사건이 독립이라는 순진한(naive) 가정을 하고 있기 때문에, hence the name.
}
10. Links en ¶
Bayes Theorem: A Framework for Critical Thinking
https://neilkakkar.com/Bayes-Theorem-Framework-for-Critical-Thinking.html
https://neilkakkar.com/Bayes-Theorem-Framework-for-Critical-Thinking.html
Bayes theorem, the geometry of changing beliefs
3Blue1Brown https://www.youtube.com/watch?v=HZGCoVF3YvM
3Blue1Brown https://www.youtube.com/watch?v=HZGCoVF3YvM
An Intuitive (and Short) Explanation of Bayes’ Theorem
https://betterexplained.com/articles/an-intuitive-and-short-explanation-of-bayes-theorem/
https://betterexplained.com/articles/an-intuitive-and-short-explanation-of-bayes-theorem/
11. Links ko ¶
https://seing.tistory.com/32
베이지언 확률은 사후확률(posterior probability)을 사전확률(prior probability)과 likelihood를 이용해서 계산할 수 있도록 해 주는 확률 변환식
베이지언 확률은 사후확률(posterior probability)을 사전확률(prior probability)과 likelihood를 이용해서 계산할 수 있도록 해 주는 확률 변환식
https://hyeongminlee.github.io/post/bnn001_bayes_rule/
Bayesian_deep_learning { Up: 심층학습,deep_learning }을 위해 알아보는
Bayesian_deep_learning { Up: 심층학습,deep_learning }을 위해 알아보는
관련:
Twins:
http://biohackers.net/wiki/BayesRule
 Bayes'_theorem
Bayes'_theorem
https://ncatlab.org/nlab/show/Bayes rule
https://everything2.com/title/Bayes%27 Theorem
 베이즈 정리
베이즈 정리
Twins:
http://biohackers.net/wiki/BayesRule
https://ncatlab.org/nlab/show/Bayes rule
https://everything2.com/title/Bayes%27 Theorem


![[http]](/123/imgs/http.png)