vector의 경우 위 둘은 ALWAYS equiv? chk
방향벡터,direction_vector tbw
직선,line의 방향벡터.
...직선에 대한 벡터방정식,vector_equation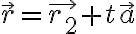 에서 벡터
에서 벡터 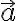 를 직선의 방향벡터(direction vector)라 한다.
를 직선의 방향벡터(direction vector)라 한다.
(Zill 6e ko p427)
}
이중벡터
바이벡터
이중벡터 via bivector ... or 바이벡터 ?
bivector ... or 바이벡터 ?
try bivector
bivector
Q: '방향벡터,direction_vector'라는 말이 있던데 (영벡터를 제외한) 모든 벡터는 방향벡터 맞나? 크기는 필요없고 방향을 봐라, 혹은 크기보다는 방향에 주목해라 이런 뉘앙스인가? see also 방향,direction
{see ![[https]](/123/imgs/https.png) 수학백과: 방향벡터 보면 직선,line에 대해서 주어지는. 따라서 직선 하나당 2개.
수학백과: 방향벡터 보면 직선,line에 대해서 주어지는. 따라서 직선 하나당 2개.
근데 자주 보이지는 않는 표현... (굳이 방향이라는 단어를 명시할 필요가 없으니) - direction.vector
direction.vector
![[https]](/123/imgs/https.png) 수학백과: 방향벡터 보면 직선,line에 대해서 주어지는. 따라서 직선 하나당 2개.
수학백과: 방향벡터 보면 직선,line에 대해서 주어지는. 따라서 직선 하나당 2개.근데 자주 보이지는 않는 표현... (굳이 방향이라는 단어를 명시할 필요가 없으니) -
직선,line의 방향벡터.
...직선에 대한 벡터방정식,vector_equation
(Zill 6e ko p427)
}
변위벡터,displacement_vector
위치벡터,position_vector r
단위벡터,unit_vector u, a, e에 아래첨자, 3차원의 경우 각각 i/j/k or x/y/z (위에 ^)
접벡터,tangent_vector T (위에 →)
단위접벡터,unit_tangent_vector T (위에 ^)
법선벡터,normal_vector N, n
단위접벡터 T(s) 라면,
단위법선벡터,unit_normal_vector N(s)=(T'(s))/(|T'(s)|)=sgn(T'(s))
종법선벡터(binormal_vector) B(s)=T(s)×N(s) (이 세 줄:![[https]](/123/imgs/https.png) 공간곡선의 Frenet frame)
공간곡선의 Frenet frame)
기울기벡터,gradient_vector
벡터장,vector_field
벡터함수,vector_function
벡터미적분,vector_calculus
벡터공간,vector_space
방향코사인,direction_cosine
분리벡터,separation_vector
separation vector
 separation vector x 2023-12-31
separation vector x 2023-12-31
 분리 벡터 = https://namu.wiki/w/분리 벡터 ... "위치벡터,position_vector에서
분리 벡터 = https://namu.wiki/w/분리 벡터 ... "위치벡터,position_vector에서  source vector 를 뺀 벡터." (Griffiths)
source vector 를 뺀 벡터." (Griffiths)
Up: 분리,separation 벡터,vector
유사벡터,pseudovector
이중벡터,bivector
{ w위치벡터,position_vector r
단위벡터,unit_vector u, a, e에 아래첨자, 3차원의 경우 각각 i/j/k or x/y/z (위에 ^)
접벡터,tangent_vector T (위에 →)
단위접벡터,unit_tangent_vector T (위에 ^)
법선벡터,normal_vector N, n
단위접벡터 T(s) 라면,
단위법선벡터,unit_normal_vector N(s)=(T'(s))/(|T'(s)|)=sgn(T'(s))
종법선벡터(binormal_vector) B(s)=T(s)×N(s) (이 세 줄:
![[https]](/123/imgs/https.png) 공간곡선의 Frenet frame)
공간곡선의 Frenet frame)기울기벡터,gradient_vector
벡터장,vector_field
벡터함수,vector_function
벡터미적분,vector_calculus
벡터공간,vector_space
방향코사인,direction_cosine
분리벡터,separation_vector
separation vector
Up: 분리,separation 벡터,vector
유사벡터,pseudovector
이중벡터,bivector
이중벡터
바이벡터
이중벡터 via
try
MKL
exterior_product { exterior_product }
exterior_product }
wedge_product { wedge_product }
wedge_product }
기하학,geometry
computer_graphics
벡터,vector
공간,space
축,axis
넓이,area > directed_area { directed area "directed area" directed area }
directed area }
평면,plane
exterior_algebra
geometric_algebra
Clifford_algebra
multivector
exterior_product {
wedge_product {
기하학,geometry
computer_graphics
벡터,vector
공간,space
축,axis
넓이,area > directed_area { directed area "directed area"
평면,plane
exterior_algebra
geometric_algebra
Clifford_algebra
multivector
}
확률벡터,random_vector
{
// tmp from random vector
random vector
유한차원확률벡터 finite dimensional random vector
무한차원확률벡터 infinite dimensional random vector
가우스 확률벡터 Gaussian random vector
}//random vector ... random vector
random vector  random vector
random vector  random vector
random vector
{
// tmp from
유한차원확률벡터 finite dimensional random vector
무한차원확률벡터 infinite dimensional random vector
가우스 확률벡터 Gaussian random vector
}//random vector ...
ADDHERE
고딩 레벨에선
예를 들어 공간의 각 점에 대한 함수(장,field)를 다음 두 방식으로 나타낸다.
=\varphi(\vec{r}))
수학에선 벡터공간,vector_space의 원소,element. ← 벡터의 정의
스칼라,scalar는 크기만 있는 것,
벡터는 크기 + 방향 (magnitude + direction)이 있는 것으로 설명
여기서 크기+방향은
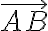 로 나타냄.
로 나타냄.
표현(representation):벡터는 크기 + 방향 (magnitude + direction)이 있는 것으로 설명
여기서 크기+방향은
(x, y) 좌표를 쓰기도 하고, (두 수 모두 크기와 방향을 나타냄)
(r, θ) 극좌표를 쓰기도 함 (r은 크기, θ는 방향,direction)
 의 크기를
의 크기를 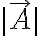 , 방향을
, 방향을 ) 로 나타내기도.
로 나타내기도.
 의 magnitude를
의 magnitude를  direction을 unit vector
direction을 unit vector 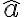 로 하면
로 하면
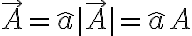 이렇게 magnitude × direction으로 나타낼 수 있음.
이렇게 magnitude × direction으로 나타낼 수 있음.
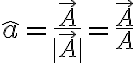 (Ulaby)
(Ulaby)
두 점,point을 통해서 나타내는 일이 잦음. 시점이 A, 종점이 B인 벡터를 (r, θ) 극좌표를 쓰기도 함 (r은 크기, θ는 방향,direction)
따라서 벡터의 합은 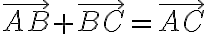 가 됨.
가 됨.
- 화살표 arrow
- 방향성 선분 (directed line segment - 방향,direction + 선분,line_segment)
예를 들어 공간의 각 점에 대한 함수(장,field)를 다음 두 방식으로 나타낸다.
// from BigBook, DELME - too easy
두 실수의 순서조 ) 를 (평면)벡터 (vector in plane)라 하고
를 (평면)벡터 (vector in plane)라 하고
![$\vec{x}=[x_1,x_2]$ $\vec{x}=[x_1,x_2]$](/123/cgi-bin/mimetex.cgi?\Large \vec{x}=[x_1,x_2]) 또는
또는 ![$\vec{x}=\left[{x_1 \atop x_2}\right]$ $\vec{x}=\left[{x_1 \atop x_2}\right]$](/123/cgi-bin/mimetex.cgi?\Large \vec{x}=\left[{x_1 \atop x_2}\right])
로 나타낸다. 이 때 실수 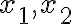 를 (평면)벡터
를 (평면)벡터 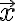 의 성분(component)이라고 한다.
의 성분(component)이라고 한다.
세 실수의 순서조 ) 를 (공간)벡터(vector in space)라 하고
를 (공간)벡터(vector in space)라 하고
![$\vec{x}=[x_1,x_2,x_3]$ $\vec{x}=[x_1,x_2,x_3]$](/123/cgi-bin/mimetex.cgi?\Large \vec{x}=[x_1,x_2,x_3]) 또는
또는 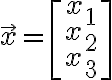
(마찬가지)
두
Contents
- 1. 관련
- 2. 행렬과의 관계
- 3. 예 (여러 벡터, 분류)
- 4. 예 (적용, 특히 물리 쪽에)
- 5. 연산
- 6. 기타 연산 비슷한 것 혹은 transform에 해당하는 것 (연산?)
- 7. 분해 (연산?)
- 8. 벡터와 각 : 직교, 평행, etc. (연산으로 분류할까?)
- 9. 벡터로 표현한 도형 TOCLEANUP
- 10. 표기 TOCLEANUP
- 11. 비교
- 12. 표현
- 13. 벡터의 삼각부등식
- 14. Links ko
- 15. links en
- 16. tmp; Sadiku 5e 1.7-1.9
- 17. 벡터의 공변성과 반변성 - covariance and contravariance
- 18. 수학/물리 바깥에서 단어 vector의 쓰임
2. 행렬과의 관계 ¶
3. 예 (여러 벡터, 분류) ¶
zero vector - 영벡터,zero_vector ![[https]](/123/imgs/https.png) 수학백과: 영벡터 https://mathworld.wolfram.com/ZeroVector.html
수학백과: 영벡터 https://mathworld.wolfram.com/ZeroVector.html
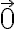 =(0,0,0)
=(0,0,0)
unit vector - 단위벡터,unit_vector
![[https]](/123/imgs/https.png) 수학백과: 영벡터 https://mathworld.wolfram.com/ZeroVector.html
수학백과: 영벡터 https://mathworld.wolfram.com/ZeroVector.htmlx1=(1,0,0)
x2=(0,1,0)
x3=(0,0,1)
sparse_vectorx2=(0,1,0)
x3=(0,0,1)
Sparse vectors are common in ML applications and often require some type of method to deal with them effectively.![[https]](/123/imgs/https.png) src
src
원소의 대부분이 0인 벡터
rel. sparsity ?
null_vector![[https]](/123/imgs/https.png) src
src원소의 대부분이 0인 벡터
rel. sparsity ?
4. 예 (적용, 특히 물리 쪽에) ¶
5. 연산 ¶
그리고 각종 lin alg package/SW/CAS (ex. 넘파이,NumPy)의 해당 문법 언급
Q; 이걸 vector algebra라고 함?
같음(상등, equality), 덧셈, 뺄셈, 실수배는 매우 쉽다. Trivial.
곱셈에 해당하는 것이 여러 가지이다.
나눗셈에 해당하는 것 있나?
같음(상등, equality), 덧셈, 뺄셈, 실수배는 매우 쉽다. Trivial.
곱셈에 해당하는 것이 여러 가지이다.
나눗셈에 해당하는 것 있나?
- 덧셈 vector_addition
- 교환법칙,commutativity 만족, commutative, a+b=b+a
- 결합법칙,associativity 만족, associative, a+(b+c)=(a+b)+c
- 덧셈의 항등원 (영벡터) 존재
기하적으로 설명할 때, triangle law + parallelogram law로 설명.
- 교환법칙,commutativity 만족, commutative, a+b=b+a
- 실수배 scalar_multiplication scalar_multiple
는 길이,length가
배,
이면 stretching,
이면 compaction? // 스케일링 scaling 스케일 scale
방향,direction은이면 그대로,
이면 반대로, ....
이면 영벡터? 암튼 곱하는 scalar의 부호,sign가 음이면 방향이 정반대로..
인 경우? 곱셈항등원1...? 아님 scalar 1은 벡터집합에 속하지 않으므로 항등원은 아니고 별도의 뭔가로 봐야 하는건지? // 항등원,identity_element 하나,one
벡터의 정규화,normalization: 상수배해서 길이를 1로 조정하는 작업. 관련: 단위벡터,unit_vector
- 뺄셈
덧셈 역원?
u+v=u+(-v)로 계산. 즉 위의 덧셈과 (-1 실수배)로.
- 곱셈에 해당하는 것 ... 1) 벡터의 스칼라배 - 스칼라와 벡터의 곱, 2) 벡터와 벡터의 곱 vector-vector multiplication:
(결과가 벡터)
(결과가 스칼라)
(1,1,...,1)이게 항등원?
- 다이아드 곱(diadic product)? -> dyadic_product { dyadic product ....
 dyadic Up: 곱,product?action=highlight&value=dyadic } // dyadic product ...
dyadic Up: 곱,product?action=highlight&value=dyadic } // dyadic product ...  dyadic product
dyadic product  dyadic product
dyadic product
스칼라곱,scalar_product,dot_product
벡터곱,vector_product,cross_product
내적,inner_product
외적,outer_product
위와의 관계는 정확히 모르겠다. 아래가 더 넓은 범위?
삼중곱,triple_product
텐서곱,tensor_product -?
- 크기, norm, 길이 - 노름,norm
성질..
..... 삼각부등식,triangle_inequality
이건 연산이라기보다는(f(벡터)=실수 연산으로 볼 수도 있지만) 속성,attribute?
단위벡터,unit_vector는 크기(? 노름? 길이?)가 1임
5.1.1. Sadiku ¶
심플하게 스칼라곱과 내적, 벡터곱과 외적을 구분하지 않는 설명.
(복습용. 아는 것은 수식/설명 모두 생략하고 생략했다고만 언급.)
(복습용. 아는 것은 수식/설명 모두 생략하고 생략했다고만 언급.)
스칼라와 벡터의 곱
(앞에서 언급했던가... 아무튼 쉬우므로 언급 x)
(앞에서 언급했던가... 아무튼 쉬우므로 언급 x)
두 벡터 (A, B)의 곱셈의 두 형태
세 벡터(A, B, C)의 곱셈의 두 형태
See 삼중곱,triple_product
| 스칼라곱 | 스칼라적 | 내적 | A·B | 결과가 스칼라 |
| 벡터곱 | 벡터적 | 외적 | A×B | 결과가 벡터 |
세 벡터(A, B, C)의 곱셈의 두 형태
| 스칼라 삼중적 | A·(B×C) | 결과가 스칼라 |
| 벡터 삼중적 | A×(B×C) | 결과가 벡터 |
내적
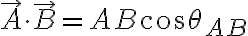
각 성분끼리 곱하는 식 생략.
내적이 0이면 직교인 것 생략.
교환법칙성립, 분배법칙성립 생략.
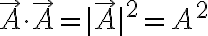 (스스로를 내적하면 크기 제곱?)
(스스로를 내적하면 크기 제곱?)
단위벡터 사이의 내적 생략.
외적
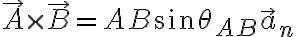
여기서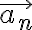 : A와 B를 포함하는 평면에 수직인 단위벡터.
: A와 B를 포함하는 평면에 수직인 단위벡터.
크기는 평행사변형 생략.
방향은 생략(오른손법칙만 알면 되니까).
행렬식 생략.
교환법칙 비성립.
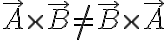
반교환법칙 성립.
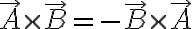
결합법칙 비성립.
 \ne (\vec{A}\times\vec{B})\times\vec{C})
분배법칙 성립.
 = \vec{A}\times\vec{B} + \vec{A}\times\vec{C})
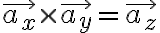 등등 생략.
등등 생략.
스칼라 삼중적
정의:
=\vec{B}\cdot(\vec{C}\times\vec{A})=\vec{C}\cdot(\vec{A}\times\vec{B}))
순환 순열방식으로 얻어짐. 평행육면체의 체적과 관련.
원문) 등등 입력하기 힘들어서 대충 알파벳을 할당해서
등등 입력하기 힘들어서 대충 알파벳을 할당해서
,\vec{b}=(g,h,i),\vec{c}=(j,k,l))
이면
=\begin{vmatrix}d&e&f\\g&h&i\\j&k&l\end{vmatrix})
벡터 삼중적
정의:
=\vec{B}(\vec{A}\cdot\vec{C})-\vec{C}(\vec{A}\cdot\vec{B}))
즉 bac-cab 법.
다음 두 식의 차이에 유의.
\vec{C} \ne \vec{A}(\vec{B}\cdot\vec{C}))
그러나
\vec{C}=\vec{C}(\vec{A}\cdot\vec{B}))
(Sadiku 5e 1.7 벡터의 곱셈)
각 성분끼리 곱하는 식 생략.
내적이 0이면 직교인 것 생략.
교환법칙성립, 분배법칙성립 생략.
단위벡터 사이의 내적 생략.
여기서
크기는 평행사변형 생략.
방향은 생략(오른손법칙만 알면 되니까).
행렬식 생략.
교환법칙 비성립.
정의:
원문
정의:
즉 bac-cab 법.
6. 기타 연산 비슷한 것 혹은 transform에 해당하는 것 (연산?) ¶
축을 중심으로 한 회전,rotation
stretch
flip (to mirror image)
관련: 행렬변환,matrix_transformation. 벡터변환이라는 것이 있다기 보다는 아마 행렬변환을 위해 벡터가 사용된다 이 정도인 듯 한데.... 그래도 벡터변환은 검색결과가 나오긴 나오는데... TOREAD.  vector.transformation
vector.transformation
벡터의 선형변환,linear_transformation에 해당하는 것은..stretch
flip (to mirror image)
transform은 수식으로는 (행렬) * (벡터) 곱 형태로 나타남.
TBW (이 tmp 섹션은 https://youtu.be/IrggOvOSZr4 보고 대충 적은 것)
7. 분해 (연산?) ¶
벡터를 각 성분(component)으로 분해할 수 있다. 벡터의 성분을 찾는 것을 resolving the vector라고 한다.
일반적으로 벡터는 직각 성분으로(i.e. 서로 직교하는 성분들로) 분해하여 사용하는 것이 편리하다. (Meriam 정역학 p4)
2차원 위의 벡터 A와 B는 이렇게 x, y성분으로 분해하고
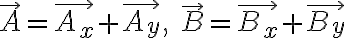
합은
+(\vec{A_y}+\vec{B_y}))
합은
and
로 나타내면 component notation
and
로 나타내면 magnitude-angle notation (관련: 극좌표,polar_coordinate 극좌표계,polar_coordinate_system)
3차원 TBW
8. 벡터와 각 : 직교, 평행, etc. (연산으로 분류할까?) ¶
| 사잇각 | 내적 | 외적 | |
| 직교, perpendicular, orthogonal | 90° | 0 | |
| 평행, parallel | 0°, 180° | 0 |
both vectors are scalars of each other일경우와 동일?
CHK
각,angle
관련:
벡터(영벡터 제외) 사이의 각은 아크코사인과 스칼라곱,scalar_product,dot_product으로 쉽게 구해진다.
3D의 경우만 보면, the angle between nonzero vectors
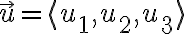 and
and 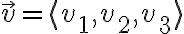
is given by
=\cos^{-1}\left( \frac{\vec{u}\cdot\vec{v}}{||\vec{u}|| \, ||\vec{v}||} \right))
Related: 코사인법칙,cosines_law
벡터(영벡터 제외) 사이의 각은 아크코사인과 스칼라곱,scalar_product,dot_product으로 쉽게 구해진다.
3D의 경우만 보면, the angle between nonzero vectors
영이 아닌 두 벡터 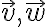 의 사이각이
의 사이각이
- 예각일 필요충분조건은
이다.
- 둔각일 필요충분조건은
이다.
- 직각일 필요충분조건은
이다.
벡터의 나란함과 평행 ...에 대해서 확실히.
일반적으로 두 벡터가 일차종속(=선형종속,linear_dependence)일 필요충분조건은 두 벡터가 나란한 것이다.
(김홍종 미적1+ p210)
9.1.1. 2차원 ¶
A를 지나고 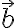 에 평행한 직선 위의 점 X가 있을 때, X의 자취의 방정식을 구하는 방법.
에 평행한 직선 위의 점 X가 있을 때, X의 자취의 방정식을 구하는 방법.
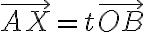
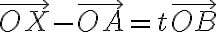
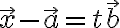
따라서,
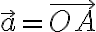 일 때, A를 지나
일 때, A를 지나 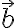 에 평행한 직선의 벡터방정식은
에 평행한 직선의 벡터방정식은
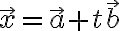 (t는 임의의 실수)
(t는 임의의 실수)
마찬가지로, A, B를 지나는 직선 위의 점 X는 다음을 만족한다.
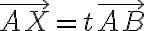
A, B, X의 위치벡터,position_vector를 각각 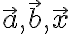 라고 하면
라고 하면
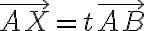
)
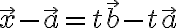
\vec{a}+t\vec{b})
이것이 두 점 A, B를 지나는 직선의 벡터방정식이다.
따라서,
점 A(x₁,y₁)을 지나고 벡터 ) 에 평행한 직선의 방정식은
에 평행한 직선의 방정식은
)
두 점 A(x₁,y₁), B(x₂,y₂)를 지나는 직선의 방정식은
)
점 ) 을 지나고 영벡터가 아닌 벡터
을 지나고 영벡터가 아닌 벡터 ) 에 수직인 직선 g의 방정식을 구하는 과정:
에 수직인 직선 g의 방정식을 구하는 과정:
A의 위치벡터를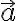 , g 위의 임의의 한 점 P의 위치벡터를
, g 위의 임의의 한 점 P의 위치벡터를 ) 라 하면
라 하면
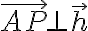
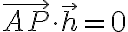
\cdot\vec{h}=0)
이때 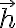 를 g의 법선벡터라고 한다.
를 g의 법선벡터라고 한다.
\cdot(a,b)=0)
+b(y-y_1)=0)
)
A의 위치벡터를
10.1. 벡터 이름 표기 ¶
이름이 v일 때
italic, arrow: 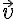 (\vec)
(\vec)
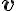 (\mathbf)
(\mathbf)
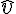 (\hat) (단위벡터)
(\hat) (단위벡터)
고등학교 교재는 이 표기법만 사용하는 듯
non-italic boldface: MimeTeX가 지원 안함, 일단 mathbf로 써 보면 이 때는 italic을 적용시키지 않는 것 같기도 한데... 예를 들어 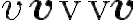 중에서 세번째.
중에서 세번째.
italic, hat: 벡터 표시를 하지 않은 그냥 문자가 그 벡터의 크기를 의미하는 표기법도 자주 쓰임
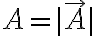
예를 들면
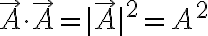
10.2. 벡터 내용 표기 ¶
앞뒤 감싸는 기호
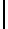 이나
이나  으로 둘러싸면 norm, 크기 - 노름,norm
으로 둘러싸면 norm, 크기 - 노름,norm
parenthesis (…)
bracket […]
\langle ... \rangle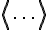 (이상 comma 사용)
(이상 comma 사용)
row_vector
column_vector (이상 comma 안씀)
또 있나?
bracket […]
\langle ... \rangle
row_vector
column_vector (이상 comma 안씀)
또 있나?
행백터/열벡터: 가로/세로?? CHK
두 점으로 벡터 표기하기?
 Euclidean_vector (==
Euclidean_vector (==  내의 두 점으로 표현되는 벡터??TOASK)의 경우 표기
내의 두 점으로 표현되는 벡터??TOASK)의 경우 표기
두 점으로 벡터 표기하기?
A: 시작점, B: 끝점

11. 비교 ¶
벡터는 방향,direction 정보에 크기(magintude) 정보도 부여한 것?
둘의 차이점은, 벡터는 절대적 위치가 아무 상관없고, 유향선분은 절대적 위치가 의미있는(중요한) ...?
12. 표현 ¶
collinear
동일 선상의, along the same straight line
같은 방향이거나 반대 방향 (either in the same or in opposite directions)
직교벡터 orthogonal vectors같은 방향이거나 반대 방향 (either in the same or in opposite directions)
서로 직교하는 벡터 둘
정규직교벡터 orthonormal vectors17. 벡터의 공변성과 반변성 - covariance and contravariance ¶
단어/표현
반변적인 contravariant
반변벡터 contravariant_vector - 이것을 보통 벡터라고 한다? (ghebook)
반변벡터 contravariant_vector - 이것을 보통 벡터라고 한다? (ghebook)
공변적인 covariant
공변벡터 convariant_vector AKA 코벡터 covector
공변벡터는 다른 말로 미분형식,differential_form 또는 1차형식(one-form) (ghebook)
공변벡터 convariant_vector AKA 코벡터 covector
공변벡터는 다른 말로 미분형식,differential_form 또는 1차형식(one-form) (ghebook)
표기
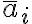 공변벡터 covariant vector
공변벡터 covariant vector
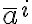 반변벡터 contravariant vector 이렇게 첨자 위 아래 여부? i는 뭐지 ??? CHK (ghebook)
반변벡터 contravariant vector 이렇게 첨자 위 아래 여부? i는 뭐지 ??? CHK (ghebook)
비디오 (Khutoryansky)
텐서 : 공변, 반변, 차수
https://www.youtube.com/watch?v=CliW7kSxxWU
basis vector(see 기저,basis)를 기반으로 contra-variant, co-variant, 텐서,tensor 같이 설명.
rank 1인 텐서는 vector.
텐서 : 공변, 반변, 차수
https://www.youtube.com/watch?v=CliW7kSxxWU
basis vector(see 기저,basis)를 기반으로 contra-variant, co-variant, 텐서,tensor 같이 설명.
rank 1인 텐서는 vector.
관련:
{
CS의 타입,type론에서 같은 단어 쓰임.
범주론(category theory)에서 함자(functor)에는 반변함자(contravariant functor), 공변함자(covariant functor)가 있음.
// 범주,category 함자,functor 반변함자,contravariant_functor, 공변함자,covariant_functor
}
텐서,tensor
좌표변환,coordinate_transformation AKA transformation of coordinates
다중선형대수,multilinear_algebra
비슷한 단어가 쓰이는 (벡터 제외한) 다른 분야: MISC TOCLEANUP좌표변환,coordinate_transformation AKA transformation of coordinates
다중선형대수,multilinear_algebra
{
CS의 타입,type론에서 같은 단어 쓰임.
tmp bmks ko
C# 제네릭에서의 불변성과 가변성 - https://www.csharpstudy.com/DevNote/Article/31
Twin
 공변성과_반공변성_(컴퓨터_과학)
공변성과_반공변성_(컴퓨터_과학)
 Covariance_and_contravariance_(computer_science)
Covariance_and_contravariance_(computer_science)
![[https]](/123/imgs/https.png) .NET documentation: Covariance and contravariance in generics
.NET documentation: Covariance and contravariance in generics
통계에서는 영단어가 공변~ 과 매우 비슷한 공분산,covariance 개념이 있는데 어떤 관련이 있는지 TBW.C# 제네릭에서의 불변성과 가변성 - https://www.csharpstudy.com/DevNote/Article/31
Twin
![[https]](/123/imgs/https.png) .NET documentation: Covariance and contravariance in generics
.NET documentation: Covariance and contravariance in generics범주론(category theory)에서 함자(functor)에는 반변함자(contravariant functor), 공변함자(covariant functor)가 있음.
// 범주,category 함자,functor 반변함자,contravariant_functor, 공변함자,covariant_functor
}
Srcs:
텐서(Tensor)와 좌표 변환(Coordinate Transformation) https://ghebook.blogspot.com/2011/06/tensor-coordinate-transformation.html
 벡터의_공변성_및_반변성
벡터의_공변성_및_반변성
표기: 텐서 미적분학(Tensor Calculus) https://ghebook.blogspot.com/2011/07/tensor-calculus.html
Twins:표기: 텐서 미적분학(Tensor Calculus) https://ghebook.blogspot.com/2011/07/tensor-calculus.html
18.1. 생명과학쪽 ¶
벡터의 어원이 대충 '나르다' '운반자' '운반해주는 역할을 하는 것' '전달자' 정도의 뜻이며, (? chk.  etymology.of.vector ) 수학에선 의미가 극도로 추상화되었지만
etymology.of.vector ) 수학에선 의미가 극도로 추상화되었지만
생물학,biology 의학 약학 등등 쪽에선 그 뜻 그대로 쓰인다.
플라스미드,plasmid 등등.
 벡터_(분자생물학)
벡터_(분자생물학)
 Vector_(molecular_biology)
Vector_(molecular_biology)
생물학,biology 의학 약학 등등 쪽에선 그 뜻 그대로 쓰인다.
플라스미드,plasmid 등등.
18.2. 컴퓨터쪽 ¶
vector_graphics - computer_graphics쪽에서. raster_graphics과 대조되는.
인터럽트벡터,interrupt_vector - rel. 인터럽트,interrupt, IVT,interrupt_vector_table, interrupt_handler
각종 PL의 vector type, ex. C++의 벡터 - std::vector ... pagename?
등등
인터럽트벡터,interrupt_vector - rel. 인터럽트,interrupt, IVT,interrupt_vector_table, interrupt_handler
각종 PL의 vector type, ex. C++의 벡터 - std::vector ... pagename?
등등
Twins:
![[https]](/123/imgs/https.png) https://en.citizendium.org/wiki/Vector_(mathematics) - easy
https://en.citizendium.org/wiki/Vector_(mathematics) - easy
 Vector - disambiguation
Vector - disambiguation
 Vector_(mathematics_and_physics)
Vector_(mathematics_and_physics)
 벡터
벡터
https://mathworld.wolfram.com/Vector.html
https://encyclopediaofmath.org/wiki/Vector - geometric
![[https]](/123/imgs/https.png) https://en.citizendium.org/wiki/Vector_(mathematics) - easy
https://en.citizendium.org/wiki/Vector_(mathematics) - easyhttps://mathworld.wolfram.com/Vector.html
https://encyclopediaofmath.org/wiki/Vector - geometric
상위:
Compare - 벡터와 대조/대비되는 것:
Compare - 벡터와 대조/대비되는 것:

