사건,event

기호
보통 대문자로 표기하는듯. Event의 앞글자 E나, A, B 등.
S : certain event (밑의 Sub 참조)
∅ : impossible or null event (밑의 Sub 참조)

(이하 - 사건의 표기와 확률의 표기의 연관성 - 이라 하면 되나?)

사건 표기중에 가능한 것 (Schaum Prob, RV and RP)
X가 확률변수,random_variable이고 x가 고정된 실수라면
(X = x)
(X ≤ x)
(X > x)
(x1 < X ≤ x2) 이런것들은 events.
그리고
사건 (X = x)의 확률은 P(X = x),
사건 (X ≤ x)의 확률은 P(X ≤ x),
…인 것.

사건의 확률 표기
사건 E의 확률,probability은
P(E), Pr(E), ℙ(E)로 표기하며,
$[0,1]$ 사이의 실수,real_number임.


정의:
확률실험,random_experiment에서, 사건은 표본공간,sample_space의 부분집합,subset.
Ex.
주사위를 던지는 시행,trial의 표본공간은 {1, 2, 3, 4, 5, 6}이며 '짝수인 눈이 나온다'는 사건
동전을 던지는 시행의 표본공간은 {H, T}이며 '앞면이 나온다'는 사건

QQQ 보통 표본공간의 모든 원소(=결과,outcome) 중에서 특정한 조건,condition을 만족하는 것을 뽑은 부분집합?

"전압이 음수이다"라는 사건은 집합 $\lbrace\zeta:-\infty<\zeta<0\rbrace$ 에 해당.
"사건이 발생했다" ⇔ "실험의 결과,outcome ζ가 사건(집합)에 속한다, 즉 ζ ∈ E"

그래서 사건의 연산은 집합,set의 연산. (set_operation .. 합집합union, 교집합intersection, 여집합complement, 차집합difference, etc.)

결과,outcome와 비슷한데 정확한 관계가....?
결과는 원소이고 사건은 결과로 이루어진 집합.



[edit]

1. Sub: 여러 사건

elementary event
discrete sample space에서 나온 single outcome으로 이뤄진 이벤트.
원소가 하나인 집합에 대응.
... singleton?
근원사건(elementary event), 근원사상, 표본점(sample point): single outcome from a discrete sample space.
//QQQ CHK 그럼
elementary event(=sample point)는 원소 수가 1인 집합이고
결과,outcome는 집합이 아닌 원소인가?
///mv to 근원사건,elementary_event

certain_event
certain event
(consists of all outcomes, always occurs)
=S(표본공간,sample_space)
contains all outcomes
전체집합,universal_set에 대응.
[https]수학백과: 전사건 aka 전체사건
전사건의 여사건은 공사건.

impossible_event
null event, impossible event
(contains no outcomes, never occurs)
has no outcome
공집합,empty_set에 대응.
A∩B=∅이면, A와 B 두 사건은 상호 배타적(mutually exclusive)이라 한다. (또는 서로소. disjoint?)
[https]수학백과: 공사건
공사건의 여사건은 전사건.

영사건
일어날 확률이 0인 사건.
공사건은 영사건이지만, 영사건이 항상 공사건인 것은 아님.
[https]수학백과: 영사건

두 사건 A, B에 대해
합사건, 합사상: A∪B
곱사건, 곱사상: A∩B
(A의) 여사건, 여사상: AC
(서로) 배반사건, 배반사상: A∩B=∅ (i.e. 곱사건이 공집합,empty_set)

여사건
여사건,complementary_event
표기법: 다양(A̅, AC, A', ￢A) (wp)
chk: 사건 A의 확률이 p이면 사건 A의 여사건의 확률은 1−p? - yes
P(AC) = 1 − P(A)
Uses: 다음 공식에 나옴: 반복시행(curr at 시행,trial), 베르누이_시행,Bernoulli_trial, ...
rel. 여집합,complement or 여집합,set_complement or 여집합,complement_set
WpKo:여사건
WpEn:Complementary_event
MKLINK: complement, logical_complement, set_complement

tail_event - writing

[edit]

2. 배반사건

A와 B가 서로 배반사건 :
A∩B = {}
따라서 그 때 다음 관계가 성립
P(A∩B) = 0,
P(A∪B) = P(A) + P(B) (배반사건의 확률, 확률의 덧셈법칙)
See [https]수학백과: 확률의 덧셈법칙 or 덧셈정리

[edit]

3. 비교: 배반사건과 독립사건

A와 B가 배반 A와 B가 독립
의미 동시에 일어나지 않는다. 일어날 확률에 서로 영향이 없다.
관계식 P(A∩B)=0 P(A|B)=P(A)
P(A∩B)=P(A)P(B)


[edit]

4. 사건의 독립 및 종속

사건 A와 B가 있다면,
P(B|A)=P(B)
일 때, 사건 B는 A에 대해 독립이다. 이 때
=P(B|AC)
도 성립한다.

사건 A, B가 서로 독립이기 위한 필요충분조건은
P(A∩B)=P(A)P(B)
이다.

독립이 아니면 두 사건은 서로 종속이라고 한다.

pf.
P(A|B)
=P(A∩B)/P(B)
=P(A)P(B)/P(B)
=P(A)
A, B가 독립이면
  • P(B|A) = P(B|AC) = P(B)
  • P(A∩B) = P(A)·P(B)
  • AC, BC도 독립

A, B 서로 독립: A⊥B로 표기
$A\bot B \Leftrightarrow \Pr(AB)=\Pr(A)\Pr(B)$
A1, A2 and A3 are independent iff
  • A1⊥A2
  • A2⊥A3
  • A3⊥A1
  • P(A1A2A3)=P(A1)P(A2)P(A3)

Events A1, A2, …, Am are independent iff
  • Every set with m-1 events from A1, …, Am are independent
  • P(A1…Am)=P(A1)P(A2)…P(Am)


이하 RR에서 옮겨옴. to merge.

[edit]

5. Mutually Exclusive Events

mutually exclusive
Two events,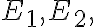 $E_1,E_2,$ such that 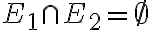$E_1\cap E_2=\emptyset$ are said to be mutually exclusive.

A collection of events, 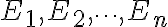$E_1,E_2,\cdots,E_n$ is said to be mutually exclusive if for all pairs,
$E_i\cap E_j=\not\bigcirc$
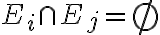
For a collection of mutually exclusive events,
$P(E_1\cup E_2\cup\cdots\cup E_n)=P(E_1)+P(E_2)+\cdots+P(E_n)$

사건,event의 mutually exclusive & collectively exhaustive한 집합을 사건공간,event_space이라고 한다.

[edit]

6. 독립사건 independent event


정의:
두 사건 $A,\,B$ 가 독립이다 iff
$P(A\cap B)=P(A)\cdot P(B)$

위 정의와 조건부확률,conditional_probability의 정의로부터 바로
$P(A|B)=P(A)$
$P(B|A)=P(B)$
임을 알 수 있음.

일반적으로는
$P(A)\ne P(A|B)$
그러나, 사건 A가 일어났다는 사실이 사건 B가 일어날 확률에 영향을 미치지 않을 경우에는
$P(B|A)=P(B)$

표본공간,sample_space(S)과 공집합,empty_set(∅)은 임의의 사건 A와 독립임.
$P(S\cap A)=P(A)=P(S)P(A)$
$P(\emptyset\cap A)=P(\emptyset)=P(\emptyset)P(A)$

세 사건 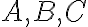$A,B,C$ 는 독립이다. iff
$P(A\cap B\cap C)=P(A)P(B)P(C)$
$P(A\cap B)=P(A)P(B)$
$P(A\cap C)=P(A)P(C)$
$P(B\cap C)=P(B)P(C)$

See also, merge: 독립성,independence#s-2



[edit]

7. 배반사건

두 사건 A와 B가 서로 배반사건:
$A\cap B=\emptyset$
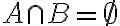
$P(A\cap B)=0$
A, B가 배반사건이면 다음 관계가 성립.
$A\subset B^c$
$B\subset A^c$

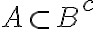
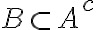
AKA 서로소인 사건, disjoint event, exclusive event (분리,disjoint. curr goto 결합,joint)


[edit]

8. 배반사건이면서 독립사건

$0=P(A\cap B)=P(A)P(B)$
- A, B중 적어도 하나의 확률은 0이어야 함

즉 P(A)>0, P(B)>0 일 때 A와 B가
독립사건이면 배반사건이 될 수 없고
배반사건이면 독립사건이 될 수 없음

[edit]

9. 사건 클래스 event class

// event_class class_of_events
// mklink 표본공간,sample_space > finite_sample_space

tmp from http://www.ktword.co.kr/abbr_view.php?m_temp1=1662
{
표본공간의 부분집합. 사건들이 모인 집합.
AKA 사건 공간(Event Space) 또는 사건 클래스(Event Class) 또는 필드(Field)
클래스,class, 체,field와 같은 단어를 쓰네? 수학의 체와 관계가?
}
tmp from Leon-Garcia 2.1.4 Event Classes
{
sample space: $S$
event: $S$ 의 부분집합

event class: 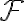$\mathcal{F}$
class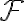 $\mathcal{F}$ of events of interest
Only events in this class are assigned probabilities.
관심이 가는 사건만 집합을 모아서 거기서만 확률을 계산하는 듯.
이 중에 일정 성질을 가지는 부분집합을 Borel field(kms: 보렐 집합체; curr goto 체,field)라 한다.
사건,event들(events: sets)의 집합(set)임. 즉 set of sets.

Notation: calligraphic 대문자를 쓰는 듯.

ex. 2.8.
coin toss의 outcome이 S={T,H}이고, S의 모든 부분집합은 event이다. S의 모든 가능한 events는?
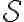$\mathcal{S}$ ={∅,{H},{T},{H,T}}
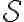즉, $\mathcal{S}$ 는 공집합과 S를 둘 다 포함한다.

유한표본공간(finite sample space) 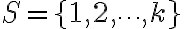$S=\lbrace 1,2,\cdots,k\rbrace$ 에 대해, S의 모든 부분집합이 사건,event이 되도록 허용한다. 이런 사건클래스(class of events)를 power set of S라 부르고 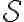$\mathcal{S}$ 로 표기한다.

즉 멱집합,power_set과 관련
}

[edit]

10. pmf와의 관계

이산확률변수,discrete_random_variable X와 실수 x에 대해, X=x일 사건이 일어날 확률,probability을 대응하는 함수 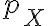$p_X$ 가 확률질량함수.
i.e.
표본공간,sample_space S에 정의된 이산확률변수 X에 대해,
사건 {X=x}={s∈S|X(s)=x} 가 일어날 확률이 확률질량함수,probability_mass_function,PMF. (수학백과: 확률질량함수)

[edit]

11. 확률론 밖의 event

[edit]

11.1. CS, programming, SW development에서