선적분은 정적분,definite_integral을 일반화한 것이다.
정적분은 피적분함수(integrand)를 (적분변수가 x이면) x축을 따라 적분한다.
선적분에서는 피적분함수를 공간(혹은 평면) 내의 곡선,curve C를 따라 적분한다. 따라서 곡선적분(curve integral)이 보다 나은 이름이지만, 선적분이 표준으로 쓰인다.
정적분은 피적분함수(integrand)를 (적분변수가 x이면) x축을 따라 적분한다.
선적분에서는 피적분함수를 공간(혹은 평면) 내의 곡선,curve C를 따라 적분한다. 따라서 곡선적분(curve integral)이 보다 나은 이름이지만, 선적분이 표준으로 쓰인다.
(Kreyszig 10.1)
t를 시간, C를 시간 t에서의 물체의 궤적,
=(x(t),y(t),z(t)))
t=a일 때의 시점(initial point),y(a),z(a)))
t=b일 때의 종점(terminal point),y(b),z(b)))
시점과 종점이 같은 경우 closed
이렇게 생각할 수 있음
(continuous, differentiable, simple, smooth는 생략 - 책 참조)
t=a일 때의 시점(initial point)
t=b일 때의 종점(terminal point)
시점과 종점이 같은 경우 closed
이렇게 생각할 수 있음
(continuous, differentiable, simple, smooth는 생략 - 책 참조)
나중에 TBW.................
(O'Neil 7e 12.1 p367)
책 앞 line integral 표기법 안내:
z축이 ) 인 그래프를 그리고 설명함
인 그래프를 그리고 설명함
)
)

2차원 평면에서 호길이,arclength의 매우 작은 변화 (미분,differential) ds는
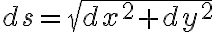 (피타고라스 정리)
(피타고라스 정리)
구하는 것은
ds) (이하 t=a에서 t=b 까지 가는 것을 곡선 C?라고 표시)
(이하 t=a에서 t=b 까지 가는 것을 곡선 C?라고 표시)
,y(t))\sqrt{dx^2+dy^2})
이것을 t에 대해 나타내야 하므로
,y(t))\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt)
위 조건에서 ,\,dy/dt=h%27(t)) ...
...
from Khan: Introduction to the line integral https://youtu.be/_60sKaoRmhU
벡터장,vector_field 안에서만 의미가 있나?
벡터장 A, 곡선 L이 주어질 때, L위의 점 a에서 b까지 움직이면서 미소길이(접선,tangent_line방향의 매우 짧은 벡터, 접벡터,tangent_vector 인지 CHK)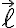 이 받는 A의 영향은 스칼라곱,scalar_product,dot_product
이 받는 A의 영향은 스칼라곱,scalar_product,dot_product
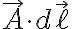
이고 이것을 선적분하면 (두번째 식은 개곡선일때만)
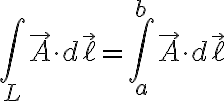
이고 폐경로일땐(원래 자리로 돌아옴, 즉 a→b→a→b..., 순환circulation)
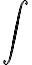 대신
대신 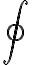
를 씀?
벡터장 A, 곡선 L이 주어질 때, L위의 점 a에서 b까지 움직이면서 미소길이(접선,tangent_line방향의 매우 짧은 벡터, 접벡터,tangent_vector 인지 CHK)
from https://www.youtube.com/watch?v=r4okf9RAVWo ; CHK
알짜힘이 다음과 같으므로
)\cdot r%27(t))
a에서 b까지 받은 바람의 영향의 총합은
)\cdot r^{\prime}(t)dt)
여기서
=\frac{dr(t)}{dt})
=r^{\prime}(t) dt)
이므로 적분식은
\cdot dr)
이 된다
from, and see also: http://mathnmath.tistory.com/100
latex 수식을 카피해 왔는데 mimetex에선 \mathbf가 일반 글자(non-bold)랑 구분이 잘 안 된다. 모두 vec으로 치환함.
scalar field에서는
vector field에서는
W = F · s 와 관련이 깊다.
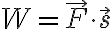
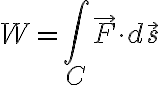
↓
선적분
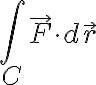
에서
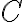 : 적분할 경로
: 적분할 경로
) : 피적분함수
: 피적분함수
특히 적분할 경로가 폐곡선인 경우, 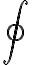 기호를 쓰며, 값을
기호를 쓰며, 값을 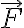 의
의 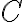 에 대한 circulation이라고 부름
에 대한 circulation이라고 부름
2020-09-16 from https://www.youtube.com/watch?v=Sa7xDuWEvZ4 스토크스 정리와 다이버젠스 정리 5:30 (차동우)
//from 수학백과 선적분
n-공간에서 정의된 연속함수,continuous_function ) 에 대하여, 곡선,curve
에 대하여, 곡선,curve ![$X:[a,b]\to\mathbb{R}^n$ $X:[a,b]\to\mathbb{R}^n$](/123/cgi-bin/mimetex.cgi?\Large X:[a,b]\to\mathbb{R}^n) 을 따르는
을 따르는  의 (선)적분은
의 (선)적분은
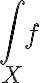 또는
또는 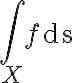
로 나타내고, (s는 호의 길이(호길이,arclength), ds는 길이원소(length element))
이 값은
) \left| X%27(t) \right| dt)
로 정의한다. 이 식을 간단히
 \right| dt)
로 쓰기로 한다.
이 값은
(김홍종 미적1+ p349)
Logs ¶
2020-09-10
한국어 설명:
https://angeloyeo.github.io/2020/08/17/line_integral.html (벡터장,vector_field의 선적분)
https://angeloyeo.github.io/2020/10/01/path_independence.html (벡터장과 path independence)
한국어 설명:
https://angeloyeo.github.io/2020/08/17/line_integral.html (벡터장,vector_field의 선적분)
https://angeloyeo.github.io/2020/10/01/path_independence.html (벡터장과 path independence)
2020-09-18
line 대신 curve 라고도 하나보다 (이게 더 옳지 않나? line은 보통 직선 뉘앙스 아닌가)
선적분 curve integral https://pinkwink.kr/215
곡선,curve
line 대신 curve 라고도 하나보다 (이게 더 옳지 않나? line은 보통 직선 뉘앙스 아닌가)
선적분 curve integral https://pinkwink.kr/215
곡선,curve
2020-12-24
단어만 보면 경로적분,contour_integral과 비슷한데 차이 구분하여 서술. Compare. TBW.
선적분 개념은 물리적으로 일,work과 밀접하다. 관계서술예정. 특히 보존력(밑에 언급).
참고: https://blog.naver.com/bmw9707121/221595571286
단어만 보면 경로적분,contour_integral과 비슷한데 차이 구분하여 서술. Compare. TBW.
선적분 개념은 물리적으로 일,work과 밀접하다. 관계서술예정. 특히 보존력(밑에 언급).
참고: https://blog.naver.com/bmw9707121/221595571286
2022-05-26
'...좀 더 보편적인 적분을(비록 경로적분,path_integral이 더 잘 어울리는 용어일지 모르겠지만) 선적분,line_integral이라고 한다. ...' (Thomas 13e ko p823)
경로,path
'...좀 더 보편적인 적분을(비록 경로적분,path_integral이 더 잘 어울리는 용어일지 모르겠지만) 선적분,line_integral이라고 한다. ...' (Thomas 13e ko p823)
경로,path
Compare: 면적분,surface_integral
Related: 보존력,conservative_force개념과 깊은 연관이 있는듯?
Related: 스토크스_정리,Stokes_theorem는 뭐뭐...의 선적분값 = 뭐뭐..의 면적분값 이라는 정리.
Related: 보존력,conservative_force개념과 깊은 연관이 있는듯?
Related: 스토크스_정리,Stokes_theorem는 뭐뭐...의 선적분값 = 뭐뭐..의 면적분값 이라는 정리.
Twins:
![[https]](/123/imgs/https.png) 두산백과: 선적분 AKA 곡선적분 - curve_integral. 사실 이게 더 정확한 표현.
두산백과: 선적분 AKA 곡선적분 - curve_integral. 사실 이게 더 정확한 표현.
![[https]](/123/imgs/https.png) 수학백과: 적분 - section "4. 곡선 위의 선적분" 참조
수학백과: 적분 - section "4. 곡선 위의 선적분" 참조
![[https]](/123/imgs/https.png) 수학백과: 선적분
수학백과: 선적분
https://everything2.com/title/Line integral
 선적분
선적분
![[https]](/123/imgs/https.png) 두산백과: 선적분 AKA 곡선적분 - curve_integral. 사실 이게 더 정확한 표현.
두산백과: 선적분 AKA 곡선적분 - curve_integral. 사실 이게 더 정확한 표현.![[https]](/123/imgs/https.png) 수학백과: 적분 - section "4. 곡선 위의 선적분" 참조
수학백과: 적분 - section "4. 곡선 위의 선적분" 참조![[https]](/123/imgs/https.png) 수학백과: 선적분
수학백과: 선적분https://everything2.com/title/Line integral

