일단 명칭은 이런데 이게 귀납법인가?
귀납가설,induction_hypothesis
{
https://proofwiki.org/wiki/Definition:Induction_Hypothesis
... induction hypothesis
induction hypothesis
가설,hypothesis
근데 이름이 가설이지만 사실 가정,assumption에 더 가까운?
AKA inductive_hypothesis ? chk
}
철학,philosophy(수리논리,mathematical_logic학을 제외한 고전적 철학)에서 말하는 귀납법이랑은 분명 다르지만 수학,math에서 귀납,induction은 (거의?) 항상 이걸 일컬음?? i.e. 수학과 철학에서 단어 induction의 의미가 다름? via 수백+내생각. chk
도미노에 비유함.여기선 교육적으로 좋지 않은 비유라 함 ... https://youtu.be/NLcv5VGGQXU (12 Math) induction은 확장 논리 보다는 축소 논리의 도구로 보는게 맞다고.
표현들:귀납가설,induction_hypothesis
{
https://proofwiki.org/wiki/Definition:Induction_Hypothesis
...
가설,hypothesis
근데 이름이 가설이지만 사실 가정,assumption에 더 가까운?
AKA inductive_hypothesis ? chk
}
https://proofwiki.org/wiki/Definition:Induction_Step
isa 귀납,induction 단계,step
} // induction step induction step
induction step
isa 귀납,induction 단계,step
} // induction step
Cmp: finite_induction (?) tmp
{
{
principle of finite induction
https://planetmath.org/principleoffiniteinduction
https://proofwiki.org/wiki/Principle_of_Finite_Induction
... finite induction
finite induction  유한귀납 ?
유한귀납 ?
}https://planetmath.org/principleoffiniteinduction
https://proofwiki.org/wiki/Principle_of_Finite_Induction
...
수학적 귀납법을 사용한 증명 방법 ¶
전제: 자연수 n에 관한 명제,proposition p(n)이 있다.
1. n=1일때 성립함을 보인다. (show)
2. n=k일때 성립한다고 가정한다. (assume)
3. n=k+1일때 성립함을 보인다. (show)
1. n=1일때 성립함을 보인다. (show)
2. n=k일때 성립한다고 가정한다. (assume)
3. n=k+1일때 성립함을 보인다. (show)
Principle of Mathematical Induction ¶
Let Sn be a 진술,statement about the positive integer n.
Suppose that
Suppose that
- S1 is true.
- Sk+1 is true whenever Sk is true.
(Stewart Calculus 7e, p.98)
Proof by induction ¶
수학적 귀납,induction법을 쓴 증명,proof법
 에 대해 성립한다.
에 대해 성립한다.
- 성질(property)이 입력 크기(input size) 1인 경우에 성립함(holds)을 증명 (base_case)
- 성질이 입력 크기
에서
까지 성립한다고 가정
- 성질이 입력 크기
에서 성립함을 보임(show)
(김황남)
Uses ¶
수학적귀납법의 사용처, 사용 예
1. 증가수열,increasing_sequence임을 밝히기
Q. Show that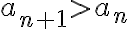 for all
for all 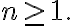
A.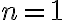 일 때 참이다.
일 때 참이다. 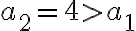 이기 때문.
이기 때문.
이것이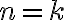 일 때 참이라고 가정하면
일 때 참이라고 가정하면
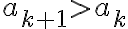
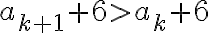
>\frac12(a_k+6))
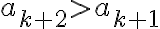
We have deduced(연역,deduction) 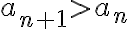 is true for
is true for 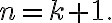 Therefore the inequality(부등식,inequality) is true for all
Therefore the inequality(부등식,inequality) is true for all  by induction.
by induction.
Q. Show that
A.
이것이
2. 그리고 저 수열이 6 미만임을 밝히기(유계,bounded 유계수열,bounded_sequence) - 모든  에 대해
에 대해 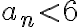
증가수열이므로 이것이 하계,lower_bound가 있음을 우리는 안다. 모든 에 대해,
에 대해, 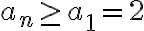 이다.
이다.
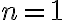 일 때
일 때 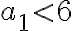 이므로 주장(assertion)이 참이다.
이므로 주장(assertion)이 참이다.
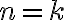 일때도 참이라 가정(suppose)한다. 그러면
일때도 참이라 가정(suppose)한다. 그러면
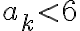
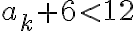
 < \frac12(12) = 6)
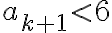
따라서 induction에 의해 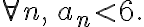
증가수열이므로 이것이 하계,lower_bound가 있음을 우리는 안다. 모든
(Stewart 9e p734)
한계, 약점, 단점 ¶
자연수에 대한 명제에만 적용 가능?
- 이 표현을 어디서 봤더라? 아무튼, 그니까... 이산적인 steps로 환원가능하고(reducible), 그 steps 사이에 명확한 점화관계(점화식,recurrence_relation) 가 있는, 이런 경우에만 사용가능. 이 생각이 맞는지? chk
other resources ¶
이것의 자연스러운 일반화: well-founded_induction - 작성중
Related:
Twins:
https://mathworld.wolfram.com/PrincipleofMathematicalInduction.html
![[https]](/123/imgs/https.png) 수학백과: 수학적 귀납법
수학백과: 수학적 귀납법
https://encyclopediaofmath.org/wiki/Mathematical_induction
https://everything2.com/title/Mathematical Induction
 수학적 귀납법
수학적 귀납법
 수학적_귀납법
수학적_귀납법
https://mathworld.wolfram.com/PrincipleofMathematicalInduction.html
![[https]](/123/imgs/https.png) 수학백과: 수학적 귀납법
수학백과: 수학적 귀납법https://encyclopediaofmath.org/wiki/Mathematical_induction
https://everything2.com/title/Mathematical Induction
https://artofproblemsolving.com/wiki/index.php/Induction
https://planetmath.org/principleoffiniteinduction
 Mathematical_induction
Mathematical_induction
 수학적_귀납법
수학적_귀납법
https://proofwiki.org/wiki/Definition:Mathematical_Induction
https://proofwiki.org/wiki/Principle_of_Mathematical_Induction
https://planetmath.org/principleoffiniteinduction
https://proofwiki.org/wiki/Definition:Mathematical_Induction
https://proofwiki.org/wiki/Principle_of_Mathematical_Induction
Up: 수학,math

