AKA 시정수, 특성시간
기호: τ (Greek tau)
RL회로,RL_circuit에서 τ=τL=L/R (유도시간상수)
τC, τL 등
RC회로,RC_circuit에서 τ=τC=RC (전기용량 시간상수)RL회로,RL_circuit에서 τ=τL=L/R (유도시간상수)
e−1=0.368
1−e−1=1−0.368=0.632
1−e−1=1−0.368=0.632
t=τ=RC일 때 e−1=0.368
따라서 시간 상수는 충전된 전하량의 63.2%가 방전되기 위한 시간. CHK
따라서 시간 상수는 충전된 전하량의 63.2%가 방전되기 위한 시간. CHK
RC회로에서 충전의 경우 - 축전기,capacitor를 충전하는.
일단 시간에 대한 전하,electric_charge의 식은 =C\mathcal{E}(1-e^{-t/RC})=C\mathcal{E}(1-e^{-t/\tau})) 이고
이고
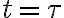 인 경우,
인 경우,
=C\mathcal{E}(1-e^{-\tau/\tau}))
)
)
)
따라서 스위치를 닫는 순간(전하가 0인 순간)에서
최대충전전하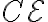 의 63.2%가 될 때 까지 걸리는 시간이 전기용량시간상수.
의 63.2%가 될 때 까지 걸리는 시간이 전기용량시간상수.
최대충전전하
그리고 시간에 대한 전류,electric_current는
=\frac{dQ}{dt}) ..... 그런데 위에서
..... 그런데 위에서 =C\mathcal{E}(1-e^{-t/RC})) 였으므로
였으므로
![$=C\mathcal{E}\left[ 0- \left( -\frac1{RC} \right) e^{-t/RC} \right]$ $=C\mathcal{E}\left[ 0- \left( -\frac1{RC} \right) e^{-t/RC} \right]$](/123/cgi-bin/mimetex.cgi?\Large =C\mathcal{E}\left[ 0- \left( -\frac1{RC} \right) e^{-t/RC} \right])
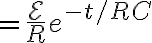
 그래프는, 처음에
그래프는, 처음에 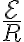 (이때가 최대전류) 부터 시작해서 감소하며
(이때가 최대전류) 부터 시작해서 감소하며
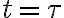 일 때 최대전류의 36.8% 가 흐른다.
일 때 최대전류의 36.8% 가 흐른다.
갈수록 전류는 0이 된다. i.e. 전류 그래프는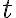 가 커질수록 0에 가까워진다. 즉
가 커질수록 0에 가까워진다. 즉 =0) 이다.
이다.
즉
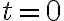 일 때
일 때 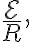
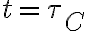 일 때
일 때 
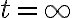 일 때
일 때 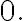
갈수록 전류는 0이 된다. i.e. 전류 그래프는
즉
시간상수란 전류가 최종 평형값 E/R의 약 63%에 도달하는 데 걸리는 시간이다.
(하이탑 물2 p133)
유도 시간상수의 물리적 의미는 RL회로,RL_circuit의
) (전류의 증가)
(전류의 증가)
식에서 알 수 있으며 유도 시간상수의 값은
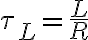
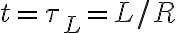 을 대입하면
을 대입하면
=0.63\frac{\mathcal{E}}{R})
결국 시간상수 τL은 회로에 흐르는 전류가 최종 평형값 ℰ/R의 약 63%에 도달하는 데 걸리는 시간.
(from Halliday)
시간상수 τ: 전류가 초기값의 1/e로 감소하는 데 걸리는 시간
(from 二友출판사 기초물리학)

