cosh의 그래프는 현수선,catenary이다.
1.2. 약간 다른 것 (CLEANUP) ¶
tanh 그래프는 arctan과 비슷, -1 < tanh x < 1, 수평점근선이 y=±1임.
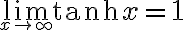
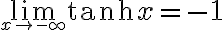
성질/정리
Hyperbolic identities
이하 두 식은 정의에서 쉽게 나온다.
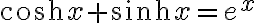

이 두 식을 곱하면,
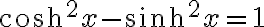
i.e.
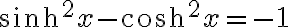
양변을 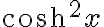 로 나누면,
로 나누면,
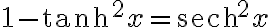
양변을 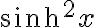 로 나누면,
로 나누면,
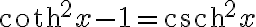
4. 테일러 급수 ¶
쌍곡선함수의 테일러 급수 전개.
테일러_급수,Taylor_series 테일러_다항식,Taylor_polynomial 테일러_전개,Taylor_expansion
Ref: https://planetmath.org/TaylorSeriesOfHyperbolicFunctions
Ref: https://planetmath.org/TaylorSeriesOfHyperbolicFunctions
Twin:
![[https]](/123/imgs/https.png) 수학백과: 쌍곡함수
수학백과: 쌍곡함수
 쌍곡선함수
쌍곡선함수
 Hyperbolic_function
Hyperbolic_function
https://ghebook.blogspot.com/2020/06/hyperbolic-function.html 쌍곡선 함수(Hyperbolic Function)
Up:
![[https]](/123/imgs/https.png) 수학백과: 쌍곡함수
수학백과: 쌍곡함수https://ghebook.blogspot.com/2020/06/hyperbolic-function.html 쌍곡선 함수(Hyperbolic Function)
----
- [1] 강우석 2021-03-18 1:12m


