합성함수,composite_function의 미분에서 나오는 방법? 합성함수의 유일한 미분법인가?
1. .... ¶
Chain rule은 Newton/Lagrange 방식의 표기보다 Leibniz 표기를 쓸 때 압도적으로 편하다 (마치 약분할 것 처럼 식을 쓸 수 있는)
정리: 함수 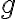 가
가 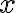 에서 미분가능하고,
에서 미분가능하고,  가
가 ) 에서 미분가능하면
에서 미분가능하면
![$\frac{d}{dx}\left[f(g(x))\right]=f'(g(x))g'(x)$ $\frac{d}{dx}\left[f(g(x))\right]=f'(g(x))g'(x)$](/123/cgi-bin/mimetex.cgi?\Large \frac{d}{dx}\left[f(g(x))\right]=f%27(g(x))g%27(x))
,\,u=g(x)) 로 두고 라이프니츠 기호로 표현하면, 위 식은
로 두고 라이프니츠 기호로 표현하면, 위 식은
![$\frac{d}{dx}\left[f(u)\right]=TBW$ $\frac{d}{dx}\left[f(u)\right]=TBW$](/123/cgi-bin/mimetex.cgi?\Large \frac{d}{dx}\left[f(u)\right]=TBW)

함수 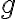 가
가 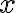 에서 미분가능하고,
에서 미분가능하고,  가
가 ) 에서 미분가능하면, 합성함수
에서 미분가능하면, 합성함수 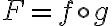 즉
즉 =f(g(x))) 는
는 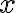 에서 미분가능하며,
에서 미분가능하며, 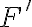 은 다음 곱,product으로 주어진다.
은 다음 곱,product으로 주어진다.
=f%27(g(x))\cdot g%27(x))
라이프니츠 표기Leibniz notation를 쓰면, 미분가능한 두 함수 ,\,u=g(x)) 에 대해
에 대해

(Stewart)
2. Multivariable chain rule ¶
If f is a real-valued fn of 3 variables u, v, and w, written in the form
,)
and the variables u, v, w are each functions of x,
,v=h(x),w=k(x),)
then by substituting g(x), h(x), and k(x) for u, v, and w, we obtain z as a function of x:
,h(x),k(x)).)
The chain rule in this case reads:
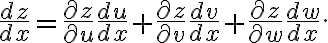
from Vector Calculus 6e p124
전미분,total_differential의 chain rule
https://mathinsight.org/chain_rule_multivariable_introduction
https://mathinsight.org/chain_rule_multivariable_examples
https://mathinsight.org/chain_rule_multivariable_examples
5. 정보이론 ¶
조건부상호정보,conditional_mutual_information의 연쇄법칙이 있음.
check out: https://www.inc.cuhk.edu.hk/InformationTheory/files/PDF/2_4.pdf
엔트로피,entropy,
상호정보,mutual_information,
조건부엔트로피,conditional_entropy
조건부상호정보,conditional_mutual_information의 chain rule이 차례로 언급
{
Chain rule for entropy:
=\sum_{i=1}^{n}H(X_i|X_1,\cdots,X_{i-1}))
ex. n=2:
=H(1)+H(2|1))
ex. n=3:
=H(1)+H(2|1)+H(3|1,2))
Chain rule for conditional entropy:
=\sum_{i=1}^{n}H(X_i|X_1,\cdots,X_{i-1},Y))
Chain rule for mutual information:
=\sum_{i=1}^{n}I(X_i;Y|X_1,\cdots,X_{i-1}))
ex. n=2:
=I(1;Y)+I(2;Y|1))
ex. n=3:
=I(1;Y)+I(2;Y|1)+I(3;Y|1,2))
Chain rule for conditional mutual information:
=\sum_{i=1}^{n}I(X_i;Y|X_1,\cdots,X_{i-1},Z))
엔트로피,entropy,
상호정보,mutual_information,
조건부엔트로피,conditional_entropy
조건부상호정보,conditional_mutual_information의 chain rule이 차례로 언급
{
Chain rule for entropy:
Chain rule for conditional entropy 증명
)
-H(Y))
,X_2,\cdots,X_n)-H(Y))
+\sum_{i=2}^{n}H(X_i|(X_1,Y),X_2,\cdots,X_{i-1})-H(Y))
+\sum_{i=2}^{n}H(X_i|X_1,\cdots,X_{i-1},Y)-H(Y))
+\sum_{i=2}^{n}H(X_i|X_1,\cdots,X_{i-1},Y))
)
다른 증명
)
 H(X_1,X_2,\cdots,X_n|Y=y))
 \sum_{i=1}^{n} H(X_i|X_1,\cdots,X_{i-1},Y=y))
 H(X_i|X_1,\cdots,X_{i-1},Y=y))
)
}
5.1. 엔트로피의 연쇄법칙 chain rules for entropy ¶
tmp from ![[https]](/123/imgs/https.png) this slide page 1
this slide page 1
{
확률변수 더미(collection)의 엔트로피,entropy는, 조건부엔트로피,conditional_entropy의 합과 같다.
The entropy of a collection of random variables is the sum of conditional
entropies.
![[https]](/123/imgs/https.png) this slide page 1
this slide page 1{
확률변수 더미(collection)의 엔트로피,entropy는, 조건부엔트로피,conditional_entropy의 합과 같다.
The entropy of a collection of random variables is the sum of conditional
entropies.
Thm: Let  be random variables having the mass probability(아마도 결합확률질량함수,joint_probability_mass_function,joint_PMF)
be random variables having the mass probability(아마도 결합확률질량함수,joint_probability_mass_function,joint_PMF) .) Then
Then
=\sum_{i=1}^{n} H(X_i|X_{i-1},\cdots,X_1))
The proof is obtained by repeating the application of the two-variable expansion rule for entropies.
}
6. NN의 backpropagation algorithm에서 나오는 chain rule ¶
일단은 http://sanghyukchun.github.io/74/ 글의 "Backpropagation Algorithm" 문단 참조. weight update의 phase 2에서 chain rule을 사용.
MKLINK:
뉴런,neuron
신경망,neural_network
손실함수,loss_function
weight parameter update (weight_parameter - 가중값,weight parameter, weight_update, ...이것들중에 pagename TBD? 아님 페이지 따로 없어도 무방할 듯.)
전파,propagation - 순전파? forward_propagaion and 역전파,backpropagation
기울기하강,gradient_descent
심층학습,deep_learning
그림의 수식을 보면 rel. - 편미분,partial_derivative, 전미분,total_derivative ... curr see Total_derivative#The_chain_rule_for_total_derivatives
Total_derivative#The_chain_rule_for_total_derivatives
뉴런,neuron
신경망,neural_network
손실함수,loss_function
weight parameter update (weight_parameter - 가중값,weight parameter, weight_update, ...이것들중에 pagename TBD? 아님 페이지 따로 없어도 무방할 듯.)
전파,propagation - 순전파? forward_propagaion and 역전파,backpropagation
기울기하강,gradient_descent
심층학습,deep_learning
그림의 수식을 보면 rel. - 편미분,partial_derivative, 전미분,total_derivative ... curr see
See also:
Twins:
https://en.citizendium.org/wiki/Chain_rule
![[https]](/123/imgs/https.png) 수학백과: 연쇄법칙
수학백과: 연쇄법칙
 연쇄_법칙
연쇄_법칙
 Chain_rule
Chain_rule
Twins:
https://en.citizendium.org/wiki/Chain_rule
![[https]](/123/imgs/https.png) 수학백과: 연쇄법칙
수학백과: 연쇄법칙AKA 체인 룰

