여기 변수  에 원주율,pi
에 원주율,pi  를 대입하면, Euler's identity(오일러_항등식,Euler_identity):
를 대입하면, Euler's identity(오일러_항등식,Euler_identity):

복소 지수와 삼각함수,trigonometric_function의 관계를 나타냄.
i, x 대신 j, θ로 다시 쓰면
cis 표기법: 오일러 공식의 함수화, cis function
=\cos(x)+i\sin(x)=e^{ix})
i.e.
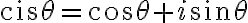
i.e.
Thomas ¶
정의. 임의의 실수 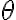 에 대해
에 대해
(유도 과정? 책에선 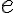 의 허수 제곱이 정의되지 않았음을 언급하며 증명이라고는 하지 않음)
의 허수 제곱이 정의되지 않았음을 언급하며 증명이라고는 하지 않음)
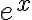 의 테일러_급수,Taylor_series
의 테일러_급수,Taylor_series
)
에서 ) 로 치환하고 간단히 고치면
로 치환하고 간단히 고치면
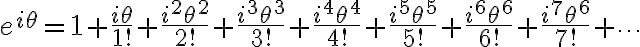
+i\left(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots\right))
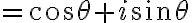
이 식으로부터 임의의 복소수,complex_number 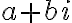 에 대하여
에 대하여 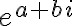 을
을  로 정의 내릴 수 있다. 아울러 식에
로 정의 내릴 수 있다. 아울러 식에 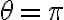 를 대입하면
를 대입하면
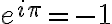
이고 이것을 변형한

은 수학에서 가장 중요한 5개의 상수,constant로 이루어져 있다. (오일러_항등식,Euler_identity)
(Thomas 13e ko chap8.10 이항급수와 테일러 급수의 활용 - 마지막 부분)
Twins:
https://mathvault.ca/euler-formula/ Euler’s Formula: A Complete Guide
https://mathworld.wolfram.com/EulerFormula.html
https://brilliant.org/wiki/eulers-formula/
https://mathvault.ca/euler-formula/ Euler’s Formula: A Complete Guide
https://mathworld.wolfram.com/EulerFormula.html
https://brilliant.org/wiki/eulers-formula/
Up: 공식,formula

