미분가능한 일변수함수 ) 에 대해 미분,differential
에 대해 미분,differential 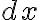 를 독립변수,independent_variable로 정의한다.
를 독립변수,independent_variable로 정의한다.
즉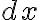 는 임의의 실수로 주어질 수 있다.
는 임의의 실수로 주어질 수 있다.
이 때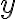 의 미분을 다음과 같이 정의한다.
의 미분을 다음과 같이 정의한다.
dx)
미분가능한 이변수함수 ) 에 대해 미분
에 대해 미분 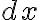 와
와 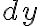 를 독립변수로 정의한다.
를 독립변수로 정의한다.
즉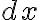 와
와 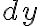 는 임의의 값으로 주어질 수 있다.
는 임의의 값으로 주어질 수 있다.
그러면 미분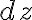 는 다음과 같이 정의되고, 이것을 전미분(total differential)이라 한다.
는 다음과 같이 정의되고, 이것을 전미분(total differential)이라 한다.
dx + f_y(x,y)dy = \frac{\partial z}{\partial x}dx + \frac{\partial z}{\partial y}dy)
때때로 기호 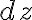 대신
대신 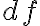 를 이용하기도 한다.
를 이용하기도 한다.
즉
이 때
즉
그러면 미분
(Stewart 8e ko p773)
변수
변수
함수값
{
}
1계 상미분방정식,ordinary_differential_equation,ODE
+N(x,y)y%27=0,\; dy=y%27dx)
i.e.
dx+N(x,y)dy=0) ......(1)
......(1)
에서 미분형식,differential_form dx+N(x,y)dy) 가
가  완전미분exact_differential, 즉 이 형식이 어떤 함수
완전미분exact_differential, 즉 이 형식이 어떤 함수 ) 의 미분
의 미분
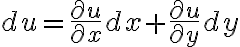 ......(2)
......(2)
이면, 이 상미분방정식을 완전미분방정식,exact_differential_equation이라고 부른다.
그러면 식 (1)은
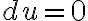
으로 쓸 수 있고, 적분하면 바로 식 (1)의 일반해를
=c)
형태로 얻는다. 이 해를 (앞서 언급된 양함수해(explicit solution)와 구별하여) 음함수해(implicit solution)라 부른다.
그러면 식 (1)은
식 (1), (2)를 비교하면, 만약 적당한 함수 ) 가 존재해서
가 존재해서
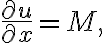
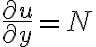 ......(4)
......(4)
이렇게 된다면, 식 (1)이 완미방(exact DE)임을 알 수 있다. 이걸로부터 다음과 같이 식 (1)이 exact DE인지 여부를 검증하는 공식을 유도할 수 있다.
식 (1)이 완미방이면, 다음 방법에 의해 함수 ) 를 구할 수 있다. 식 (4a)로부터
를 구할 수 있다. 식 (4a)로부터 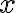 에 대해 적분하여
에 대해 적분하여
) ......(6)
......(6)
여기서 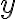 는 상수로 간주되어야 하고
는 상수로 간주되어야 하고 ) 는 적분상수 역할을 한다.
는 적분상수 역할을 한다. ) 를 결정하려면 식 (6)에서 ∂u/∂y를 이끌어 내고, 식 (4b)에서
를 결정하려면 식 (6)에서 ∂u/∂y를 이끌어 내고, 식 (4b)에서 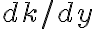 를 구한 다음,
를 구한 다음, 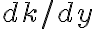 를 적분하여
를 적분하여  를 얻는다.
를 얻는다.
마찬가지로 식 (4b)에서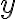 에 대해 적분하여
에 대해 적분하여
)
) 를 결정하기 위해서는 ∂u/∂x를 이끌어 내고, 식 (4a)를 써서
를 결정하기 위해서는 ∂u/∂x를 이끌어 내고, 식 (4a)를 써서 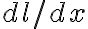 를 구한 다음 적분한다.
를 구한 다음 적분한다.
마찬가지로 식 (4b)에서
이변수 연속 함수 ) 에서
에서
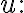
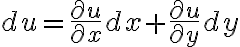
principal part in the change in 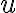 로 불리기도 한다고.
로 불리기도 한다고.
....
아무튼 그래서 total differential of 그리고 미분연산자,differentiation_operator 얘기도 나오는데,
위 전미분 식에서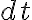 를 나누면
를 나누면
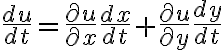
그래서 이변수연속함수의 미분연산자는 이렇게된다??
http://www.math.odu.edu/~jhh/Volume-1.PDF p159-160
위 전미분 식에서
TBW, MKLINK
Twins:
 Total_differential redir. to
Total_differential redir. to  Differential_of_a_function#Differentials_in_several_variables
Differential_of_a_function#Differentials_in_several_variables
![[https]](/123/imgs/https.png) 두산백과: 전미분 total differential
두산백과: 전미분 total differential
![[https]](/123/imgs/https.png) 수학백과: 전미분 (hard)
수학백과: 전미분 (hard)
https://planetmath.org/totaldifferential (Synonym: exact differential)
https://mathworld.wolfram.com/TotalDifferential.html (자체 내용은 없고 다른 페이지 링크, exact differential 포함)
![[https]](/123/imgs/https.png) 두산백과: 전미분 total differential
두산백과: 전미분 total differential![[https]](/123/imgs/https.png) 수학백과: 전미분 (hard)
수학백과: 전미분 (hard)https://planetmath.org/totaldifferential (Synonym: exact differential)
https://mathworld.wolfram.com/TotalDifferential.html (자체 내용은 없고 다른 페이지 링크, exact differential 포함)
Up:
Compare:
Compare:


