AKA 전기 퍼텐셜
전위: 단위 전하당 전기위치에너지
(전위) = (전기위치에너지) / (전하)
(electric potential) = (electric potential energy) per (charge)
(전위) = (전기위치에너지) / (전하)
(electric potential) = (electric potential energy) per (charge)
전기력,electric_force이 일정하게(시간에 따라 변하지 않는다는 뜻? 아님 점전하의 위치에 따라 변하지 않는다는 뜻?) 작용하는 공간에서,
전기력의 영향을 받지 않는 무한히 먼 지점(기준점)으로부터 +1 C의 단위점전하가 갖는 전기적 위치에너지(퍼텐셜에너지,potential_energy > 전기퍼텐셜에너지,electric_potential_energy)를 간단히 전위라고 한다.
전기력의 영향을 받지 않는 무한히 먼 지점(기준점)으로부터 +1 C의 단위점전하가 갖는 전기적 위치에너지(퍼텐셜에너지,potential_energy > 전기퍼텐셜에너지,electric_potential_energy)를 간단히 전위라고 한다.
전기력이 존재하는 공간에서 1C의 전하를 이동시키는 데 1J의 에너지,energy를 소모했다면 이 때의 전위는
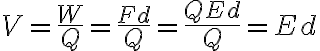
이미 전위를 갖고 있는 단위점전하가 이동할 때,
처음 단위점전하가 갖고 있던 전위) 와 이동 후의 단위점전하가 갖는 전위
와 이동 후의 단위점전하가 갖는 전위 ) 의 차이,difference를 전위차,electric_potential_difference
의 차이,difference를 전위차,electric_potential_difference 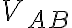 라고 한다.
라고 한다.
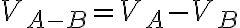
전기장 내 두 지점 사이 전위차는 전압,voltage과 같은 의미로 해석할 수 있다.
처음 단위점전하가 갖고 있던 전위
(1V의 정의) 단위점전하 1C을 옮기는 데 1J의 일,work이 필요할 때 두 점 사이의 전위차를 1V라고 정의.
![$1[{\rm V}]=\frac{1[{\rm J}]}{1[{\rm C}]}$ $1[{\rm V}]=\frac{1[{\rm J}]}{1[{\rm C}]}$](/123/cgi-bin/mimetex.cgi?\Large 1[{\rm V}]=\frac{1[{\rm J}]}{1[{\rm C}]})
전위가 같은 점을 연결하여 생기는 면(곡면,surface)을 등전위면(equipotential surface)이라고 한다. - equipotential_surface
- 등전위면 위에 있는 모든 점에서는 전위가 같다.
- 등전위면 위의 모든 점들의 전위차는 0V.
- 등전위면을 따라 전하를 이동시킬 때 한 일은 0J.
- 등전위면은 전기력선과 수직으로 교차.
- 전기장 안에서 전하는 등전위면과 수직으로 힘을 받는다. (전기력선의 방향이 어디를 향하는지 생각하면 명확)
dimension은 일이(에너지가) 아니라 에너지 나누기 전하.
기호:
스칼라량.
V
) 도 표기하는것같은데? (차동우)
도 표기하는것같은데? (차동우)
단위:...q:전위가 V, 전위차가 ΔV인가? 아님 둘다 그냥 V인가?
전위를 장으로 나타낼 때는 V (volt)
1 V = 1 J/C
스칼라임 (벡터가 아님)1 V = 1 J/C
chk - 전위는 에너지 개념(따라서 스칼라)이고, 전기장은 힘의 개념(따라서 벡터)이다. 라는 말이 맞는지.
스칼라 퍼텐셜.스칼라량.
부호,sign가 있음: 양이나 음일 수 있음.
전위는 (+)전하 근처로 갈수록 높고, (-)근처로 갈수록 낮다.
전위(electric potential) = 전기퍼텐셜에너지(electric potential energy) / 전하,electric_charge
1C당 1J의 에너지이면, 1V.
1 V = 1 J / C
1C당 1J의 에너지이면, 1V.
1 V = 1 J / C
W=qV에서
W 대신 U를 쓰는 일도 자주 있음 (그냥 일,work이라기보다는, 퍼텐셜에너지,potential_energy니까?)
V = W/q단위는 1 V = 1 J/C
W 대신 U를 쓰는 일도 자주 있음 (그냥 일,work이라기보다는, 퍼텐셜에너지,potential_energy니까?)
V = U/q그리고 델타를 V와 U에 붙이는 듯
ΔV = ΔU/q
voltage = energy / charge
V=Ed
q: 이것은 parallel plate capacitor에서만 성립하나?
일정한 전기장에서만 성립하나?
일정한 전기장에서만 성립하나?
Contents
- 1. 균일한 전기장 내에서의 전위 (장인수)
- 2. Schaum Electromagnetics
- 3. 전위(전기퍼텐셜)와 전기퍼텐셜에너지의 비교
- 4. Richardson
- 5. Urone
- 6. Bauer
- 7. Tipler
- 8. wpko 전위
- 9. absolute potential 절대전위? 절대퍼텐셜? 절대전기퍼텐셜?
- 10. 황종승
- 11. 전위의 차이, 전위차, 전압
- 12. 전위의 변화, potential changes
- 13. 전기장과 전위의 관계
- 14. Bauer
- 15. DELME ... later
- 16. 전하,electric_charge 주위의 전위
- 17. EP와 EPE의 관계? TODO
- 18. tmp
- 19. W=qV
- 20. 등전위
- 21. Links
- 22. 점전하에 의한 전위 / 점전하 주위의 전위
- 23. 전기력이 한 일
- 24. from 기초물리학(二友출판사)에서
- 25. 전위경도? 전위기울기? EP gradient
- 26. (계속; to merge) Potential Gradient, 전위경도, 전위기울기, 퍼텐셜 기울기, 퍼텐셜기울기, 전위의 기울기
- 27. 관련 pages, links ko, TMP TOREAD
- 28. 생물학의 퍼텐셜/전위
- 29. QQQ
1. 균일한 전기장 내에서의 전위 (장인수) ¶
균일한 전기장(E) 내에서의 전위(V)
일은
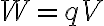
그리고
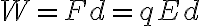
위 두 식에서 (우변)

따라서 전기장은
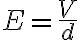 (주로 나란한 평행 금속판 사이에서 쓰임)
(주로 나란한 평행 금속판 사이에서 쓰임)
비교(전기장의 또 다른 식)
 (주로 점전하에 대해 쓰임)
(주로 점전하에 대해 쓰임)
2. Schaum Electromagnetics ¶
단위전하(unit charge)를 전기장,electric_field 안의 점 B에서 A로 옮기는 데 드는 일,work을, B에 대한 A에서의 퍼텐셜이라 하고
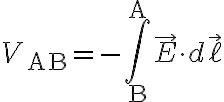
VAB
로 표기한다. 값은 다음 선적분,line_integral과 같다.3. 전위(전기퍼텐셜)와 전기퍼텐셜에너지의 비교 ¶
Compare: 전위와 전기위치에너지(전기퍼텐셜에너지,electric_potential_energy)는 다름.
전기퍼텐셜은 단위 전하(q)당 전기퍼텐셜에너지(W).
(전기퍼텐셜에너지=W, 단위전하=q, 전기퍼텐셜=V라면
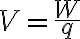 (바로 위 설명)
(바로 위 설명)
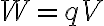 (알고 있던 식)
(알고 있던 식)
CHK)
전기퍼텐셜은 단위 전하(q)당 전기퍼텐셜에너지(W).
(전기퍼텐셜에너지=W, 단위전하=q, 전기퍼텐셜=V라면
5. Urone ¶
전위(전기퍼텐셜) V
(electric potential V) = (퍼텐셜에너지,potential_energy) / (unit charge)
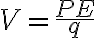
근데 PE ∝ q라서, V는 q에 의존하지 않는다.
(electric potential V) = (퍼텐셜에너지,potential_energy) / (unit charge)
(Urone)
7. Tipler ¶
From Tipler 764p
Def: potential difference
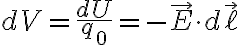
Def: finite potential difference
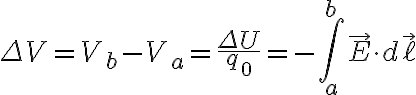
From Tipler 769p
Potential due to a system of point charges
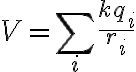
8. wpko 전위 ¶
from  전위 so CHK
전위 so CHK
{
한 점전하에 의해 생기는 전위
(무한히 먼 곳의 전위는 0이라고 가정. 진공에 점전하 q가 있을 때, r만큼 떨어진 곳의 전위 V는:)
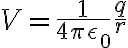
여러 점전하에 의해 생기는 전위
(qi=각 전하의 전하량, ri=전위를 구할 지점에서 각 전하까지의 거리)
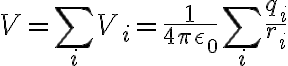
연속적인 전하 분포의 경우
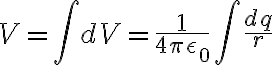
}
{
한 점전하에 의해 생기는 전위
(무한히 먼 곳의 전위는 0이라고 가정. 진공에 점전하 q가 있을 때, r만큼 떨어진 곳의 전위 V는:)
(qi=각 전하의 전하량, ri=전위를 구할 지점에서 각 전하까지의 거리)
9. absolute potential 절대전위? 절대퍼텐셜? 절대전기퍼텐셜? ¶
// 바로 위 section과 식이 동일해서 여기 적음.
absolute_potential
{
기호: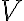
absolute_potential
{
기호:
어떤 점에서 absolute potential이란, 단위 양 시험전하(unit positive test charge)를 무한히 먼 곳에서 그 점 까지 옮겨오기 위해, 전기장을 거슬러 한 일.
진공 속에 점전하 q가 있고, 이 점전하에서 거리 r만큼 떨어진 곳에 점 P가 있다고 가정. 그러면 전하 q로 인한 점 P에서 absolute potential은
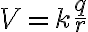
여기서 k는 쿨롱 상수.
무한히 먼 곳 (r=∞)에서 absolute potential은 0(zero).
무한히 먼 곳 (r=∞)에서 absolute potential은 0(zero).
어떤 점에서, 여러 점전하에 의한 absolute potential은
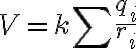
여기서 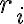 들은 전하
들은 전하 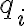 들의 그 점에서부터의 거리들임.
들의 그 점에서부터의 거리들임.
(직역인데 좀 더 다듬으면, i.e.)
여기서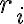 란, 각 전하
란, 각 전하 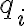 의 그 점에서부터 거리임.
의 그 점에서부터 거리임.
(직역인데 좀 더 다듬으면, i.e.)
여기서
Negative q's contribute negative terms to the potential. 양의 q도 마찬가지. (결국 q의 부호를 따지지 않고 그냥 더하면 된다는 얘기인듯.)
균일하게 대전된 구(uniformly charged sphere)에 의한 점의 absolute potential은,
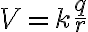
여기서 q는 구 표면의 (전체?)전하. 점은 구 표면이어도 되고 구 밖이어도 된다고. 이 퍼텐셜은 점전하 q가 구의 중심에 있는 경우와 동일. (가우스법칙?)
}
(Schaum College Phy: Absolute Potential, p84-85)
}
(Schaum College Phy: Absolute Potential, p84-85)
10. 황종승 ¶
먼저 정전위치에너지란..
전기장 내 어떤 점에 시험전하 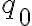 가 있다면 정전기력(curr goto 전기력)을 받을 것이다. 정전기력은 보존력이므로, 그 점의 위치에너지(see PE, EPE)가 정의된다. 위치에너지는 두 지점의 차이로 정의된다. 정의는 다음과 같다.
가 있다면 정전기력(curr goto 전기력)을 받을 것이다. 정전기력은 보존력이므로, 그 점의 위치에너지(see PE, EPE)가 정의된다. 위치에너지는 두 지점의 차이로 정의된다. 정의는 다음과 같다.
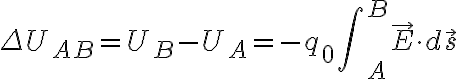
(단위는 에너지이므로 J)
Coulomb force가 하는 일 WC는
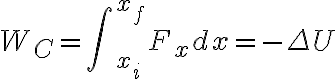
전위는
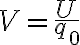
(단위는 J/C=V)
전위차는
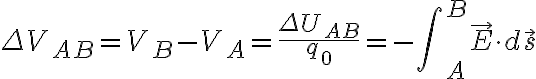
전기장이 한 일은, 점 A와 B가 다음과 같을 때 (+q는 고정, q0는 이동인 듯)
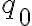 가 A에서 B로 이동할 때
가 A에서 B로 이동할 때
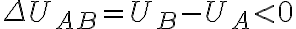 i.e.
i.e. 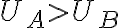
그럼 전기장이 한 일은
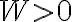
(cf. B에서 A로 이동했다면 외부에서 전기장에 일을 해준 것이므로
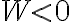 )
)
일,work W와 위치에너지 ΔU의 부호는 반대.

마이너스가 붙는 이유:
q0의 부호가 반대라면.... 또 달라지는데....
힘들어서 캡쳐.....이미지의 위 절반만 바로 위에 정리한거임. TODO 나머지도정리

아무튼 결론은 W=-ΔU
...q0....
*---------------+-----------+-------
+q A B
전위는 A>B이다. (easy) 일을 했다면 전체 에너지는 감소,
일을 받았다면 전체 에너지는 증가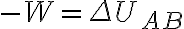
일을 받았다면 전체 에너지는 증가
| q0의 이동 | 일의 주체? | 일의 부호 | |
| A→B | 전기장이 일을 함 | W>0 | ΔUAB=UB-UA<0 |
| B→A | 전기장이 일을 받음 | W<0 | ΔUBA=UA-UB>0 |
q0의 부호가 반대라면.... 또 달라지는데....
힘들어서 캡쳐.....이미지의 위 절반만 바로 위에 정리한거임. TODO 나머지도정리

아무튼 결론은 W=-ΔU
비교:
전기장,electric_field(E) : 전기력,electric_force(F)을 만드는 물리적 상태
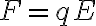
전위,electric_potential(V) : 정전위치에너지(U)를 만드는 물리적 상태
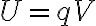
이상 src: 전위(1)전위,electric_potential(V) : 정전위치에너지(U)를 만드는 물리적 상태
11. 전위의 차이, 전위차, 전압 ¶
전위는 특히 그 차이,difference가 중요.
전위의 차이 = 전위차 = 전압,voltage
두 점 A와 B사이의 전위차 정의:
균일한 전기장 E 내의 두 점 A와 B사이의 전위차:
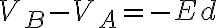
Up: 퍼텐셜차(이) potential_difference
{
Up: 퍼텐셜,potential 차이,difference
}
균일한 전기장 E 내의 두 점 A와 B사이의 전위차:
{
Up: 퍼텐셜,potential 차이,difference
}
12. 전위의 변화, potential changes ¶
위 전위의 차이와 비슷해서 여기 넣음
| R | v=R·i | 전위변화? voltage drop? |
| L | v=L·(di/dt) | 전위변화? voltage drop? |
| C | i=C·(dv/dt) | 이건 번외?? |
이 내용 맞는지? CHK TBW 필요 없으면 삭제
see also: 전압,voltage#s-10(전압강하 voltage drop) 의 식들과는 어떤 관계?
mklink 전압강하,voltage_drop
13. 전기장과 전위의 관계 ¶
전위는 전기장,electric_field이 있으면 생김
(전민용)
| 전위 V | 전기장,electric_field E |
| 스칼라 함수 | 벡터 함수 |
| 계산이 간편 | 계산이 복잡 |
| 전기장/전하 | 전위*전하 |
| Volt | Volt/Coulomb |
The 일,work done to move a unit charge from point B to point A in an 전기장,electric_field is called the potential of point A with reference to point B and shown by
(Schaum Electromagnetics)
양전하에 작용하는 힘은 E의 방향과 일치.
음전하에 작용하는 힘은 E의 방향에 반대.
(Richardson)
음전하에 작용하는 힘은 E의 방향에 반대.
(Richardson)
전위(EP)의 단위는 V, J/C
전기장의 단위는 N/C, V/m
전기장의 단위는 N/C, V/m
14. Bauer ¶
전기퍼텐셜(이하 EP)
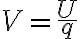
U는 q에 비례하므로, V는 q에 무관한 양이다.
i.e.
전기퍼텐셜에너지,electric_potential_energy(EPE, U)는 전하(q)에 비례하므로, 전위(V)는 전하(q)에 무관하다.
i.e.
전기퍼텐셜에너지,electric_potential_energy(EPE, U)는 전하(q)에 비례하므로, 전위(V)는 전하(q)에 무관하다.
초기점과 최종점 사이의 전기퍼텐셜차는
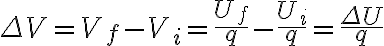
이것을 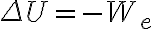 와 결합하면, EP의 변화와 전기장,electric_field이 전하에 한 일,work의 관계
와 결합하면, EP의 변화와 전기장,electric_field이 전하에 한 일,work의 관계
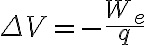
를 얻는다. EPE를 무한대에서 0으로 잡으면 한 점의 전기퍼텐셜은
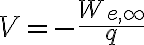
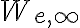 : 전하를 무한대의 한 점으로 옮길 때 전기장이 전하에 한 일
: 전하를 무한대의 한 점으로 옮길 때 전기장이 전하에 한 일
전기퍼텐셜은 양, 음, 0의 값을 가질 수 있지만, 방향은 없다.
EP의 단위는
EP의 단위는
V=J/C
15. DELME ... later ¶
시험전하,test_charge q0가 전기장 E 안에 놓여 있으면, 시험 전하가 받는 전기력은
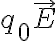
이 전기력에 의해 시험 전하가 미소변위 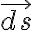 만큼 이동하면, 전기장이 전하에 한 일은
만큼 이동하면, 전기장이 전하에 한 일은
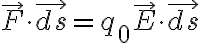
전하-전기장의 위치 에너지 변화는
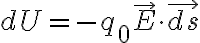
시험 전하가 A에서 B로 이동할 때, 위치에너지의 변화 ΔU=UB-UA는
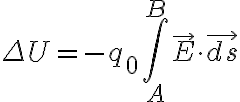
힘 q0E가 보존력이므로 이 선적분은 A와 B사이의 경로에 무관하다.
물리량
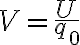
물리량
U/q0
을 전위라 한다.from Young 13e 768p

16. 전하,electric_charge 주위의 전위 ¶
(+) 전하 주위는 전위가 높고
(-) 전하 주위는 전위가 낮음
(-) 전하 주위는 전위가 낮음
점전하 Q로부터 r만큼 떨어진 점의 전위는
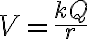
(Richardson)
18. tmp ¶
전위는 다른 퍼텐셜에너지,potential_energy와 마찬가지로
...........이 문단은 왜 에너지를 얘기하고 있지? 전기퍼텐셜(전위)와 전기퍼텐셜에너지,electric_potential_energy는 다른 것인데....???? TOCLEANUP
...........이 문단은 왜 에너지를 얘기하고 있지? 전기퍼텐셜(전위)와 전기퍼텐셜에너지,electric_potential_energy는 다른 것인데....???? TOCLEANUP
전위를 특히 전기회로에서는 비공식적으로 전압,voltage이라 부른다.
(College Physics, Giambattista, p. 346)
20. 등전위 ¶
전위차이가 없는 두 지점을 등전위라고 함.
등전위면: 3차원에서 전위가 같은 지점을 이어준 면 (equipotential surface)
등전위선: 2차원에서 전위가 같은 지점을 이어준 곡선
등전위선: 2차원에서 전위가 같은 지점을 이어준 곡선
등전위(면/선)상의 모든 점은 전위가 같으므로, 그것을 따라 전하를 이동시키는 데 하는 일은 0이다.
22. 점전하에 의한 전위 / 점전하 주위의 전위 ¶
전하량이 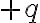 인 점전하에서
인 점전하에서  만큼 떨어진 곳의 전위는
만큼 떨어진 곳의 전위는
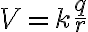
From: Young 13e 762p
Potential V due to a single point charge q
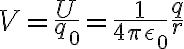
Potential due to a collection of point charge
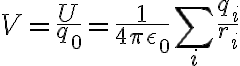
Potential due to a continuous distribution of charge
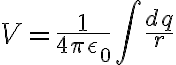
Potential V due to a single point charge q
24. from 기초물리학(二友출판사)에서 ¶
거리 r인 곳에서 점전하에 의한 전위는
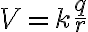
미소전하요소 dq와 임의의 점(P) 사이 거리가 r일 때 P에서 전위는
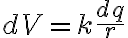 에서
에서
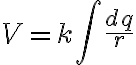
전기장 내 두 점 사이의 거리가 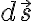 일 때 두 점 사이의 전위는
일 때 두 점 사이의 전위는
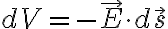
전기장이 x 성분만 있다면
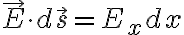 에서
에서
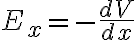
전하분포가 구대칭이라면
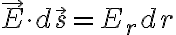 에서
에서
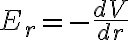
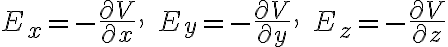
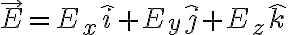
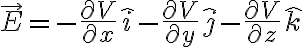
25. 전위경도? 전위기울기? EP gradient ¶
Electric Potential Gradient, EP Gradient
선속,flux과 관련된듯
주로 biology의 cell membrane 얘기가 많이 나오는데 삭제?
https://m.blog.naver.com/bmw9707121/221604351617 에 의하면
{
전위와 전기장,electric_field은
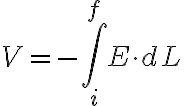
관계이고 (전위차의 미소증가) = -E·dL 즉
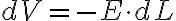
이고 편미분,partial_derivative의 연쇄법칙,chain_rule에 따르면
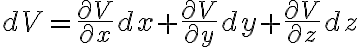
이므로
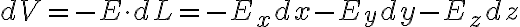
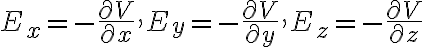
이므로 벡터로 전기장 E를 표현하면
)
i.e. grad(기울기,gradient)를 적용하면
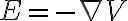
즉 전기장은 전위의 경도(기울기)의 음
}
{
전위와 전기장,electric_field은
}
26. (계속; to merge) Potential Gradient, 전위경도, 전위기울기, 퍼텐셜 기울기, 퍼텐셜기울기, 전위의 기울기 ¶
이름이 왜케 많아...수학회에는 번역 없음
Potential Gradient 전위경사도
문제: 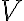 를 알 때
를 알 때 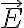 는?
는?
그리하여
그럼 이것의 최대값은?
다시말해 E와 dL이 정반대방향이면, dV/dL이 maximum값 E를 가진다.
그래서, 전기장의크기:  전위의 변화율이 가장 큰... 단위는 V/m
전위의 변화율이 가장 큰... 단위는 V/m
방향: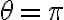 경사가 가장 가파른 방향과 정반대의 방향.
경사가 가장 가파른 방향과 정반대의 방향.
등전위면이면 다음 식이 항상 0이라고 한다방향:
ie. E는 등전위면에서 dL과 항상 수직???
그럼 등전위면에서 나오는데 수직인 방향인 벡터 N으로 표현하면
V가 증가하는 방향으로의 변화율은
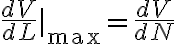
그리하여
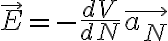 i.e.
i.e. 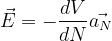
V가 증가하는 방향으로의 변화율은
그리하여
V와 E의 관계.
전계세기(벡터E)와 전위(V)와의 관계:
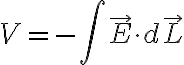
이걸 보면 V가 주어졌을 때 E를 구하는 것보다
E가 주어졌을 때 V를 구하는 것이 쉬움을 알 수 있음
E가 주어졌을 때 V를 구하는 것이 쉬움을 알 수 있음
27.1. 1 ¶
http://www.ktword.co.kr/abbr_view.php?m_temp1=3992&id=318
https://m.blog.naver.com/bmw9707121/221604351617 (bos의 스터디룸)
{ 에 따르면
이걸 두번이나 tex typesetting으로 받아적었음. 지우거나 병합....TODO
https://m.blog.naver.com/bmw9707121/221604351617 (bos의 스터디룸)
{ 에 따르면
이걸 두번이나 tex typesetting으로 받아적었음. 지우거나 병합....TODO
우선 전위(V)와 전기장(세기) ) 의 관계는
의 관계는
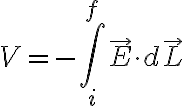
전위차의 미소증가량 dV:
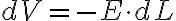
편미분,partial_derivative#s-4의 연쇄법칙,chain_rule#s-2에서
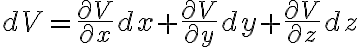
이므로
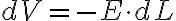
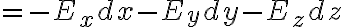
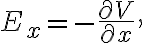
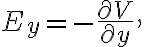
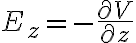
이므로 벡터로 E를 표기하면
)
그래서
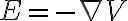
}
27.2. 2 ¶
전위의 정의.
전기장,electric_field의 회전은 0이고
폐곡선을 따라 전기장을 선적분,line_integral한 값이 0이므로,
전기장은 어떤 스칼라함수의 기울기,gradient로 표현될 것이다.
이 스칼라함수가 바로 전위이고,
전위차를 전압,voltage으로 부름.
전기장,electric_field의 회전은 0이고
폐곡선을 따라 전기장을 선적분,line_integral한 값이 0이므로,
전기장은 어떤 스칼라함수의 기울기,gradient로 표현될 것이다.
이 스칼라함수가 바로 전위이고,
전위차를 전압,voltage으로 부름.
(O는 퍼텐셜이 0이 되는 지점)
선적분의기본정리에 의해
-V(a)=\int_a^b\nabla V \cdot dl)
정의대로 직접 계산하면
-V(a)=-\int_O^b E \cdot dl + -\int_O^a E\cdot dl = -\int_a^b E\cdot dl)
따라서
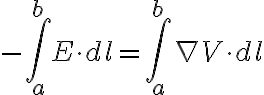
이므로
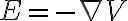
음의 부호가 필요한 이유는 '보존력이 일을 하면 퍼텐셜에너지가 감소하므로'
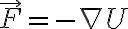
전기력도 마찬가지로
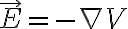
....
선적분의기본정리에 의해
저 페이지 4. 에서 설명하길, E와 V의 관계와
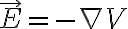 (본문에는 여기 왜 -가 없지? chk)
(본문에는 여기 왜 -가 없지? chk)
가우스_법칙,Gauss_s_law의 미분형인
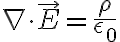
를 종합하면
=-\nabla^2 V)
그래서 푸아송_방정식,Poisson_equation과
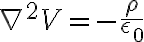
라플라스_방정식,Laplace_equation을 얻는다.

푸아송(포아송) eq는, 전하밀도,charge_density(ρ)를 알 때 전위 V를 알아내기 위해 세우는(?) 방정식이라고.
라플라스 eq는, 어떤 원천전하(naver 국어사전 왈: 특정 공간상에 전기장을 만들어 내는 전하. 대략 영어로 아마 source charge?)가 만들어 내는 전기적 효과를 주위에서 알고 싶을 때, 원천전하가 없는 주위 어떤 지점을 선택해, 그곳에는 전하가 없어서 전하밀도(=Poisson eq의 우변의 분자)가 0이기에 우변이 0이다, 이렇게 식을 두고 푸는 방정식에 해당한다 함.
라플라스 eq는, 어떤 원천전하(naver 국어사전 왈: 특정 공간상에 전기장을 만들어 내는 전하. 대략 영어로 아마 source charge?)가 만들어 내는 전기적 효과를 주위에서 알고 싶을 때, 원천전하가 없는 주위 어떤 지점을 선택해, 그곳에는 전하가 없어서 전하밀도(=Poisson eq의 우변의 분자)가 0이기에 우변이 0이다, 이렇게 식을 두고 푸는 방정식에 해당한다 함.
5. 에는 전위 식 =...) 들이 있는데
들이 있는데
- 연속분포에 의한 전위
- 면전하(밀도?)에 의한 전위
- 부피전하에 의한 전위
- 선전하에 의한 전위
// poisson, laplace eq 관련 메인 내용은 현재 방정식,equation#s-11에 있음
29. QQQ ¶
AKA 전기 퍼텐셜, electric potential, electric field potential, electrostatic potential
Twins:
tmp
http://contents.kocw.or.kr/KOCW/document/2014/gacheon/ohchangheon1/4.pdf
http://www.ktword.co.kr/test/view/view.php?no=3992
 전위
전위
tmp
http://contents.kocw.or.kr/KOCW/document/2014/gacheon/ohchangheon1/4.pdf
http://www.ktword.co.kr/test/view/view.php?no=3992
Up:
퍼텐셜에너지,potential_energy (이거 틀린 듯 DELME. at 2020-11-15)
전자기학,electromagnetism
스칼라,scalar
퍼텐셜,potential
전자기학,electromagnetism
스칼라,scalar
퍼텐셜,potential
----
- [1] 두산백과


![[http]](/123/imgs/http.png)
![[https]](/123/imgs/https.png)