2차원: 접선,tangent_line
(x-x_0))
3D: 접평면,tangent_plane
(x-x_0)+\left(\frac{\partial f}{\partial y}\right)(y-y_0))
그러나 4D 이상은 잘 모르겠다. 4D: 접공간,tangent_space { RR: 접공간,tangent_space } ...(???) CHK
1. 단어 탄젠트,tangent의 느낌 ¶
한 점,point에서 만난다, 접한다, 정도. 영어로는 touch, touching. kiss라는 표현도 봄.
라틴어 tangens (뜻: touching) 에서 유래. (Stewart)
2. 정의 ¶
The tangent line to the curve ) at the point
at the point )) is the line through
is the line through 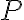 with slope
with slope
-f(a)}{x-a})
provided that this limit exists. (Stewart)
5. parametric curve에서 ¶
곡슨이 수평접선 혹은 수직접선을 갖는 조건은
horizontal_tangent
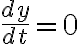
provided that
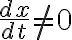
vertical_tangent
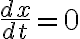
provided that
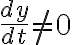
만약 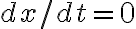 그리고
그리고 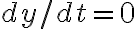 이면 접선 기울기를 결정하기 위해서는 다른 방법이 필요.
이면 접선 기울기를 결정하기 위해서는 다른 방법이 필요.
provided that
provided that
.....
일계도함수와 이계도함수
일계도함수는
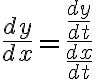
if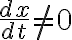
이계도함수는 위 식의 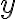 자리에
자리에 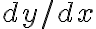 를 대입하면 된다.
를 대입하면 된다.
=\frac{\frac{d}{dt}\left(\frac{dy}{dx}\right)}{\frac{dx}{dt}})
주의:
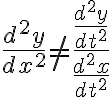
(Stewart 9e chap10.2 p673)
if
7. Compare: ¶
법선,normal_line
접평면,tangent_plane
할선,secant_line {Related: 현,chord}
곡선,curve의 한 점에서, 그 접선과 법선은 수직.
접벡터,tangent_vector접평면,tangent_plane
할선,secant_line {Related: 현,chord}
see also 해석기하_공식
----
- [1] 서울대기초수학학습교재 p103

