양의 실수  에 대해, 실수 집합에서 정의된 함수
에 대해, 실수 집합에서 정의된 함수
=a^x)
| 지수함수 exponential function | |
| 지수,exponentiation | |
| 멱함수,power_function |
(
표기:
=x\quad\quad(x>0))
)=x\quad\quad(x\in\mathbb{R}))
^n)
ex, exp(x)
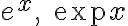
정의:general exponential function
1. 넘나 쉬운 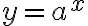 의 그래프 ¶
의 그래프 ¶
여기서 a>0, a≠1이라는 전제 있음
(밑이 1이면 상수함수,constant_function)
밑이 음수이면? QQQ 밑이 음수인 지수함수 ... // 확장,extension? 일반화,generalization?
밑이 음수인 지수함수 ... // 확장,extension? 일반화,generalization?
(밑이 1이면 상수함수,constant_function)
밑이 음수이면? QQQ
| 정의역 | 실수,real_number 전체, | |
| 치역 | 양의 실수 전체, |
| 증가함수 | |
| 감소함수 |
9. Related ¶
지수함수의 역함수,inverse_function는 로그함수,logarithmic_function
{
자연로그함수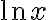 와 자연지수함수
와 자연지수함수 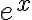 는 역함수 관계.
는 역함수 관계.
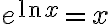 (모든
(모든 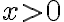 에 대해)
에 대해)
=x) (모든
(모든  에 대해)
에 대해)
마찬가지로, 로그함수와 지수함수의 역함수 관계.
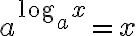 (모든
(모든 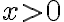 에 대해)
에 대해)
=x) (모든
(모든  에 대해)
에 대해)
(Thomas)
}
{
자연로그함수
}
임의의 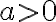 과
과  에 대해,
에 대해,
밑이 인 지수함수를 다음과 같이 정의한다.
인 지수함수를 다음과 같이 정의한다.
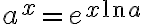
(Thomas)
밑이
우변은
^x=a^x)
Up: 함수,function


![[https]](/123/imgs/https.png)