최대최소정리,extreme_value_theorem,EVT

함수 $f(x)$ 가 $[a,b]$ 에서 연속이면 $f(x)$ 는 이 구간에서 반드시 최대값과 최소값을 가짐.
‘실수의 완비성’을 사용해서 증명한다.
고등학교 수준에선 증명할 수 없다고 함.

닫힌구간 $[a,b]$ 에서 연속인 함수는 그 구간에서 absolute_maximum value와 absolute_minimum value를 가진다. (Briggs Calculus Thm 4.1)

If $f$ is continuous on a closed interval $[a,b],$
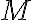then $f$ attains both an absolute_maximum value $M$ and an absolute_minimum value 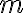$m$ in $[a,b].$
That is, there are numbers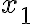 $x_1$ and $x_2$ in $[a,b]$ with $f(x_1)=m,\,f(x_2)=M,$ and $m\le f(x)\le M$ for every other $x$ in $[a,b].$
(Thomas 11e)

관련: 극값,extremum(extreme value, 극대값+극소값), 최대최소,maximum_and_minimum

실수의 완비성(completeness), 완비성 공리: 완비성,completeness

//수백
EVT는 연속함수,continuous_function의 중요한 성질로, 연속함수가 최대값과 최소값을 가질 조건,condition을 말해주는 정리.

최대값·최소값 정리는 닫힌구간이 아니거나 연속이 아닌 경우 성립하지 않을 수 있다.[1]
TBW - example?

AKA 최대값·최소값 정리
AKA 극값정리? yes. 극값문제(kms)

증명에 필요한 개념들. 먼저 다음을 알아야 한다
증가/감소
단조함수 monotone -> 단조함수,monotonic_function { MERGE WITH 함수,function#s-8 ; 단조성,monotonicity 함수,function WpSimple:Monotonic_function WpKo:단조함수 WpSimple:Monotonic_function }
순단조함수 strictly monotone
Bolzano-Weierstrass theorem = 볼차노-바이어슈트라스_정리
이건 먼저 다음을 알아야 한다: 폐구간 수렴 정리(Nested Interval Theorem)
임의의 유계,bounded인 수열은 수렴하는 부분수열을 갖는다
boundedness theorem


----
  • [1] 서울대기초수학학습교재 p93