어떤 함수와 유사한 다항식,polynomial.
from 수학백과 테일러 다항식
{
단 그 함수는 충분한 횟수로?? 미분가능한 함수여야되고 x 위치는 특정한 x=... 근방에서?
1차일 때는 선형근사,linear_approximation(함수는 선형화,linearization)이고 그걸 일반화한게 n차일 때의 테일러 근사(함수는 테일러 다항식)?
}
{
단 그 함수는 충분한 횟수로?? 미분가능한 함수여야되고 x 위치는 특정한 x=... 근방에서?
1차일 때는 선형근사,linear_approximation(함수는 선형화,linearization)이고 그걸 일반화한게 n차일 때의 테일러 근사(함수는 테일러 다항식)?
}
The nth Taylor polynomial of ex at 0 is
고등학생을 위한 고급미적 ¶
또한
TOCLEANUP completely ¶
다항식이
=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0)
이고 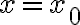 일 때의 모양을 알기 위하여?
일 때의 모양을 알기 위하여? ) 를 지나는 여러 선을 생각??
를 지나는 여러 선을 생각??
즉 상수함수, degree 0 polynomial
즉 접선,tangent_line, degree 1 polynomial
...계속 이 짓거리를 해서 점점 근접하게 만들 수 있다. 근사,approximation
Stewart ¶
테일러_급수,Taylor_series의 나머지 항 공식.
테일러 급수:
}(a)}{n!}(x-a)^n)
 번째까지의 부분합,partial_sum은
번째까지의 부분합,partial_sum은  th-degree Taylor polynomial of
th-degree Taylor polynomial of  at
at 
=f(a)+\frac{f%27(a)}{1!}(x-a)+\frac{f%27%27(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n)
그래서
=T_n(x)+R_n(x))
구간,interval 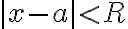 에서
에서 =0) 을 보이면 그 구간에서
을 보이면 그 구간에서  가 테일러 급수의 합과 같음을 안다.
가 테일러 급수의 합과 같음을 안다.
그렇다면 나머지 항(remainder term) ) 식은
식은
(Thm 1) }) 이
이  를 포함한 개구간
를 포함한 개구간  에서 연속이고,
에서 연속이고, 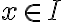 일 때
일 때
=\frac{1}{n!}\int_a^x (x-t)^n f^{(n+1)} (t)dt)
이것을 수학적귀납법,mathematical_induction으로 증명함.
...
이후 weighted 평균값정리,mean_value_theorem,MVT 소개되고
...
이후 weighted 평균값정리,mean_value_theorem,MVT 소개되고
(Thm 4) }) 이
이  를 포함한 개구간
를 포함한 개구간  에서 연속이고,
에서 연속이고, 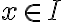 일 때,
일 때, ) such that
such that
=\frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1})
(Lagrange’s form of the remainder term)
증명은 파일 참조.


![[https]](/123/imgs/https.png)