An arc (symbol: ⌒) is a connected subset of a differentiable curve. (Wikipedia)
호의 길이 arc length ¶
정의:
\;\;(a\le x \le b) "$y=f(x)\;\;(a\le x \le b)$")
에 대해 호의 길이 함수(arc length function) s는
=\int_a^x\sqrt{1+(f%27(t))^2}dt "$s(x)=\int_a^x\sqrt{1+(f'(t))^2}dt$")
성질:
)^2} "$\frac{ds}{dx}=\sqrt{1+(f'(x))^2}$")
)^2}dx "$ds=\sqrt{1+(f'(x))^2}dx$")
^2}dx "$ds=\sqrt{1+\left(\frac{dy}{dx}\right)^2}dx$")
근호 안으로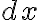 
가 들어가면,
^2+(dy)^2} "$ds=\sqrt{(dx)^2+(dy)^2}$")
양변을 제곱하면,
^2=(dx)^2+(dy)^2 "$(ds)^2=(dx)^2+(dy)^2$")
호의 길이는
^2}dx=\int ds "$L=\int_a^b\sqrt{1+\left({dy\over dx}\right)^2}dx=\int ds$")
이것의 의미는 나중에 선적분,line_integral을 배우면 이해가 잘 된다고 한다. 아무튼 현재는 호의길이함수를 적분하는것....이 호의길이???
이상 정적분,definite_integral이 쓰였음.
see also 곡선,curve#s-4.1
① ,\; a\le x \le b "$y=f(x),\; a\le x \le b$")
^2}\,dx "$\int_a^b \sqrt{ 1+\left({dy\over dx}\right)^2}\,dx$")
② ,\; c\le y \le d "$x=g(y),\; c\le y \le d$")
^2}\,dy "$\int_c^d \sqrt{ 1+\left({dx\over dy}\right)^2}\,dy$")
③ ,\,y=g(t),\;\alpha\le t\le\beta "$x=x(t),\,y=g(t),\;\alpha\le t\le\beta$")
^2 + \left({dy\over dt}\right)^2}\,dt "$\int_{\alpha}^{\beta}\sqrt{\left({dx\over dt}\right)^2 + \left({dy\over dt}\right)^2}\,dt$")
// from 강우석 2021-03-24 17m
Twins:
cartesian form = rectangular form : (x,y) or (x,y,z) 좌표를 쓰는 함수나 관계![[https]](/123/imgs/https.png)
src
parametric form =이게나옴.. 별도의 중요한 단어는 아닌 듯
극형식,polar_form
}
https://www.mathwords.com/a/arc_length_of_a_curve.htm
{rectangular form, parametric form, polar form 세 가지로 나누어 설명
cartesian form = rectangular form : (x,y) or (x,y,z) 좌표를 쓰는 함수나 관계
srcparametric form =
이게나옴.. 별도의 중요한 단어는 아닌 듯극형식,polar_form
}
Sub:
호,arc 중에서 원,circle의 일부인 것
호의 길이 arc length - 호길이,arclength - 길이,length, curr. goto 곡선,curve#곡선의길이
{곡선의 길이와 거의 동의어로 쓰이는 것 같음. arc length보다 curve length가 더 포괄적인 단어?
원,circle의 일부분일 경우 원호,circular_arc.호,arc 중에서 원,circle의 일부인 것
부채꼴(sector, esp. circular sector)에서 반지름 r이고 각 θ인 원호의 길이는 rθ