확률은 보통 probability지만..... stochastic, random으로 번역되는 경우가 상당수 있음.
i.e.
확률에 가장 잘 대응하는 단어는 보통 probability지만..... stochastic, random 역시 한국어로 번역할 때 확률로 번역되는 경우가 상당수 있음. (특히 -변수, -과정. 그렇지 않은 다른 번역: stochastic은 추계학적인, random은 무작위의, ...)
i.e.
확률에 가장 잘 대응하는 단어는 보통 probability지만..... stochastic, random 역시 한국어로 번역할 때 확률로 번역되는 경우가 상당수 있음. (특히 -변수, -과정. 그렇지 않은 다른 번역: stochastic은 추계학적인, random은 무작위의, ...)
확률론 probability_theory :
QQQ
{
확률 변수 중 한 변수만 고려한? CHK
해당하는 확률분포,probability_distribution는 주변확률분포,marginal_probability_distribution
- mathematical study of
 uncertainty
uncertainty
- probability theory provides the framework for quantifying and manipulating uncertainty
QQQ
정의역을 사건의 집합, 공역을 ![$[0,1]$ $[0,1]$](/123/cgi-bin/mimetex.cgi?\Large [0,1]) 의 집합으로 하는 함수,function라고 볼 수 있는가?? 아님 결과값만 확률이라고 부르는 것인가?
의 집합으로 하는 함수,function라고 볼 수 있는가?? 아님 결과값만 확률이라고 부르는 것인가?
'확률함수'가 정의역을 RV로 하고 치역이 확률인건가?
CHK
Sub:'확률함수'가 정의역을 RV로 하고 치역이 확률인건가?
CHK
{
확률 변수 중 한 변수만 고려한? CHK
해당하는 확률분포,probability_distribution는 주변확률분포,marginal_probability_distribution
그렇다면 편미분,partial_derivative과 유사성이 있는 / 비교할 가치가 있는 건지?
}
}
결합확률,joint_probability
조건부확률,conditional_probability
확률변수,random_variable
확률함수,probability_function
전확률정리,total_probability_theorem
확률공간,probability_space
확률적자료구조,probabilistic_data_structure - curr. 자료구조,data_structure
기하학적 확률 / 기하적 확률
관련 페이지:조건부확률,conditional_probability
확률변수,random_variable
확률함수,probability_function
전확률정리,total_probability_theorem
전확률(total probability): P(B) = ∑ P(Ai) P(B|Ai)
확률분포,probability_distribution확률공간,probability_space
확률적자료구조,probabilistic_data_structure - curr. 자료구조,data_structure
기하학적 확률 / 기하적 확률
뷔퐁의 바늘 문제(Buffon's needle problem) - 원주율,pi 추정,estimation/근사,approximation
베르트랑의 역설(Bertrand paradox) - 역설,paradox
베르트랑의 역설(Bertrand paradox) - 역설,paradox
Contents
1. 표기 ¶
이산확률변수 X가 어떤 값 x를 취할 확률:
)
연속확률변수 X에 대해 a≤X≤b가 될 확률:
)
사건(event) E에 대해 E의 확률 표기: P(E) 또는 Pr(E)
A, B의 결합확률,joint_probability: P(AB) 또는 P(A∩B)
A일 때 B의 조건부확률,conditional_probability: P(B|A)
2. 용어 ¶
사건,event
disjoint 배반?? CHK
확률의 독립: see 독립,independent
확률변수,random_variable
disjoint 배반?? CHK
확률의 독립: see 독립,independent
확률변수,random_variable
이항확률변수
이산확률변수/연속확률변수
베르누이_시행,Bernoulli_trial이산확률변수/연속확률변수
TBW
빈도,frequency와의 관계. 확률의 고전적 정의가 상대빈도의 극한?
확률에 대한 두 관점/학파/approach: 빈도주의(frequentist) vs 베이지안(Bayesian)
표본공간(sample space, Ω 또는 S): 확률 실험에서 발생 가능한 모든 결과들의 집합
사건(event): 표본공간 내에서 우리가 관심을 가지는 부분집합
빈도,frequency와의 관계. 확률의 고전적 정의가 상대빈도의 극한?
확률에 대한 두 관점/학파/approach: 빈도주의(frequentist) vs 베이지안(Bayesian)
http://m.kisdi.re.kr/mobile/colm/pro_view.m?seq=29947&category=W&selectPage=1
via https://junklee.tistory.com/124
표본공간,sample_spacevia https://junklee.tistory.com/124
표본공간(sample space, Ω 또는 S): 확률 실험에서 발생 가능한 모든 결과들의 집합
사건(event): 표본공간 내에서 우리가 관심을 가지는 부분집합
3. 용어+설명 ¶
실험(experiment): 생략 - see 확률실험,random_experiment
사건,event: 표본공간의 부분집합
(ex. 동전 세 개 던지기)
시행,trial: 생략(ex. 각 시행은 동전 한 개를 던지는 것)
표본공간,sample_space: 실험에서 나올 수 있는 모든 결과들의 모임인 집합,set S(ex. S={(H,H,H),(H,H,T),(H,T,H),(H,T,T),(T,H,H),(T,H,T),(T,T,H),(T,T,T)}, n(S)=8)
수형도(tree diagram): 나올 수 있는 모든 결과를 결정하는 편리한 방법 중 하나사건,event: 표본공간의 부분집합
(ex. A={(H,H,T),(H,T,H),(T,H,H)})
확률,probability(ex. =\frac{n(A)}{n(S)}=\frac38) )
)
Ref. 10개의 특강... (7강: 확률) 앞부분4. 사전확률 vs 사후확률 ¶
사전확률
사후확률
사후확률
prior posterior
a priori a posteriori
a priori a posteriori
Bayesian_statistics 관련. (curr see 베이즈_정리,Bayes_theorem
later see also 베이즈_확률론,Bayesian_probability, 베이즈_추론,Bayesian_inference etc.)
later see also 베이즈_확률론,Bayesian_probability, 베이즈_추론,Bayesian_inference etc.)
5. 확률론의 용어 tmp TOCLEANUP ¶
확률론 기호 : 용어
Ω : the set of all outcomes (=sample space)
ζ : individual outcome
certain subset of Ω : event
the empty set ∅ : null event
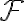 : field : a set of subsets of Ω : Ω의 부분집합들의 집합
: field : a set of subsets of Ω : Ω의 부분집합들의 집합
Ω : the set of all outcomes (=sample space)
ζ : individual outcome
certain subset of Ω : event
the empty set ∅ : null event
ℱ is assumed to be a σ-algebra, meaning it satisfies the following axioms
- Ω ∈ ℱ
- If A∈ℱ then AC∈ℱ
- If A, B ∈ ℱ then A∪B∈ℱ.
Also if A1, A2, … is a sequence of elements in ℱ then
Ω={H,T}
ℱ={{H},{T},{H,T},∅}
ℱ={{H},{T},{H,T},∅}
조건부확률 conditional probability 조건부확률,conditional_probability
조건(condition)이 A일 때.
A가 일어났을 때 B의 확률은
![$P[B|A]=\frac{P[AB]}{P[A]}\textrm{, if}P[A]>0$ $P[B|A]=\frac{P[AB]}{P[A]}\textrm{, if}P[A]>0$](/123/cgi-bin/mimetex.cgi?\Large P[B|A]=\frac{P[AB]}{P[A]}\textrm{, if}P[A]>0)
결합확률 joint probability
![$P[AB]=P[B|A]P[A]=P[A|B]P[B]$ $P[AB]=P[B|A]P[A]=P[A|B]P[B]$](/123/cgi-bin/mimetex.cgi?\Large P[AB]=P[B|A]P[A]=P[A|B]P[B])
독립 independence
Two events A, B are said to be independent iff
![$P[AB]=P[A]P[B]$ $P[AB]=P[A]P[B]$](/123/cgi-bin/mimetex.cgi?\Large P[AB]=P[A]P[B])
![$P[B|A]=P[B]$ $P[B|A]=P[B]$](/123/cgi-bin/mimetex.cgi?\Large P[B|A]=P[B])
![$P[A|B]=P[A]$ $P[A|B]=P[A]$](/123/cgi-bin/mimetex.cgi?\Large P[A|B]=P[A])
조건(condition)이 A일 때.
A가 일어났을 때 B의 확률은
Two events A, B are said to be independent iff
6. 확률의 공리적 정의 ¶
1. P(A)≥0
2. Sequence of disjoint events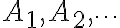
=\sum_i P(A_i))
3. P(Ω)=1
2. Sequence of disjoint events
(Ω: sample space)
표본공간의 확률은 항상 1.
표본공간의 확률은 항상 1.
1. \ge 0)
2.=1)
3.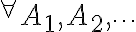
=\sum_{i=1}^{\infty}P(A_i))
S: 표본공간
2.
3.
1. 0 ≤ P(A) ≤ 1.
2. P(S) = 1.
3. If A and B are events that cannot occur simultaneously, then P(A ∪ B) = P(A) + P(B).
2. P(S) = 1.
3. If A and B are events that cannot occur simultaneously, then P(A ∪ B) = P(A) + P(B).
| Axiom I | |
| Axiom II | |
| Axiom III | If |
| Axiom III' | If |
Axioms of Probability
Probability is a number that is assigned to each member of a collection of events from a random experiment that satisfies the following properties:
If S is the sample space and E is any event in a random experiment,
(1) P(S) = 1
(2) 0 ≤ P(E) ≤ 1
(3) For two events E1 and E2 with E1 ∩ E2 = ∅
(Applied Statistics and Probability for Engineers, 6E, p55)(2) 0 ≤ P(E) ≤ 1
(3) For two events E1 and E2 with E1 ∩ E2 = ∅
P(E1 ∪ E2) = P(E1) + P(E2)
7. 공리에서 나오는 성질 ¶
성질 (고딩 교과서)
1. 0 <= P(A) <= 1
2. P(반드시 일어나는 사건)=1
3. P(절대 일어날 수 없는 사건)=0
2. P(반드시 일어나는 사건)=1
3. P(절대 일어날 수 없는 사건)=0
공리적 확률의 성질
nonnegative.
9. 확률의 덧셈정리 addition rule for probability ¶
2개의 사건에 대해
P(A∪B)=P(A)+P(B)−P(A∩B)
3개의 사건에 대해
n개의 사건에 대해
TBW
P(A∪B)=P(A)+P(B)−P(A∩B)
3개의 사건에 대해
n개의 사건에 대해
TBW
10. 독립시행의 확률 ¶
1회 시행에서 사건 A가 일어날 확률이 p일 때,
n회 독립시행에서 사건 A가 r회 일어날 확률은 (r=0,1,2,…,n)
^{n-r})
See also 이항분포,binomial_distribution
n회 독립시행에서 사건 A가 r회 일어날 확률은 (r=0,1,2,…,n)
11.1. 다항확률법칙 multinomial probability law ¶
다항확률법칙 multinomial probability law
{
확률실험의 표본공간 가
가
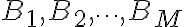 으로 분할,partition되었고,
으로 분할,partition되었고,
![$P[B_j]=p_j$ $P[B_j]=p_j$](/123/cgi-bin/mimetex.cgi?\Large P[B_j]=p_j) 이고,
이고,
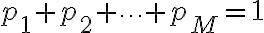 (각 사건이 mutually exclusive) 이고,
(각 사건이 mutually exclusive) 이고,
 회의 독립 실험을 했다고 가정한다.
회의 독립 실험을 했다고 가정한다.
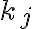 는 사건
는 사건 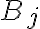 가 일어나는 횟수이면, 벡터
가 일어나는 횟수이면, 벡터 ) 은 각 사건
은 각 사건 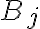 가 일어나는 횟수를 표시한다. 벡터
가 일어나는 횟수를 표시한다. 벡터 ) 은 다음 다항확률법칙을 만족한다.
은 다음 다항확률법칙을 만족한다.
![$P[(k_1,k_2,\cdots,k_M)]=\frac{n!}{k_1!k_2!\cdots k_M!}p_1^{k_1}p_2^{k_2}\cdots p_M^{k_M}$ $P[(k_1,k_2,\cdots,k_M)]=\frac{n!}{k_1!k_2!\cdots k_M!}p_1^{k_1}p_2^{k_2}\cdots p_M^{k_M}$](/123/cgi-bin/mimetex.cgi?\Large P[(k_1,k_2,\cdots,k_M)]=\frac{n!}{k_1!k_2!\cdots k_M!}p_1^{k_1}p_2^{k_2}\cdots p_M^{k_M})
)
{
확률실험의 표본공간
binomial probability law는 multinomial probability law에서 M=2인 경우.
(번역 대충이라 틀릴 수 있음)
}
(번역 대충이라 틀릴 수 있음)
}
(Leon-Garcia: Multinomial Probability Law)
11.2. 기하확률법칙 geometric probability law ¶
처음 성공할 때 까지 계속 반복, 그 횟수가 m. 횟수가 실험의 결과(outcome). 표본공간은 ℕ1. 확률 p(m)은 m-1번 동안 실패하고 마지막 한번(m번째) 성공한 것이므로 이 사건(event)의 확률은
![$p(m)=P[A_1^c A_2^c \cdots A_{m-1}^c A_m]=(1-p)^{m-1}p$ $p(m)=P[A_1^c A_2^c \cdots A_{m-1}^c A_m]=(1-p)^{m-1}p$](/123/cgi-bin/mimetex.cgi?\Large p(m)=P[A_1^c A_2^c \cdots A_{m-1}^c A_m]=(1-p)^{m-1}p)
확률의 합은 1이 된다. q=1-p일 때,
=p\sum_{m=1}^{\infty}q^{m-1}=p\frac1{1-q}=1)
성공할 때 까지 K번 초과의 시행(trial)이 필요할 확률은
![$P[\left{m>K\right}]=p\sum_{m=K+1}^{\infty}q^{m-1}$ $P[\left{m>K\right}]=p\sum_{m=K+1}^{\infty}q^{m-1}$](/123/cgi-bin/mimetex.cgi?\Large P[\left{m>K\right}]=p\sum_{m=K+1}^{\infty}q^{m-1})
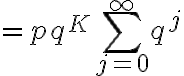
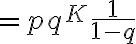
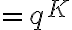
(Leon-Garcia, 2.6.4)
관련: 기하분포,geometric_distribution
관련: 기하분포,geometric_distribution
15. Misc ¶
Words of estimative probability (WEP) (del ok)
이것은 (단어, 어구, 표현, ...)과 미래 (사건,event, ...)의 확률,probability, 가능도,likelihood를 연결짓는, 추정,estimation에 대한? ambiguity, uncertainty, 등을 피하고 weasel words 등을 배제하고자 하는...
 Words_of_estimative_probability
Words_of_estimative_probability
via estimative probability :
estimative probability :
https://subsurfwiki.org/wiki/Words_of_estimative_probability
이것은 (단어, 어구, 표현, ...)과 미래 (사건,event, ...)의 확률,probability, 가능도,likelihood를 연결짓는, 추정,estimation에 대한? ambiguity, uncertainty, 등을 피하고 weasel words 등을 배제하고자 하는...
via
https://subsurfwiki.org/wiki/Words_of_estimative_probability

