R.V. 또는 RV
이하 정의역,domain을, 쉬운 설명에서는 표본공간이라 하고 어려운 설명에서는 확률공간이라 하는데 정확히 어떤 관계인지.....chk
기호: 대개 
일반 정규분포,normal_distribution의 확률변수는 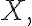
표준정규분포,standard_normal_distribution의 확률변수는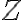 를 쓰는 관례가 있는 듯?
를 쓰는 관례가 있는 듯?
그 외의 분포에 대한 확률변수 기호 TBW
정의:표준정규분포,standard_normal_distribution의 확률변수는
그 외의 분포에 대한 확률변수 기호 TBW
표본공간에서 실수로 가는 함수.
// Schaum Prob RV and RP
random variable) 는, single-valued real function.
는, single-valued real function.
sample space 의 sample point
의 sample point 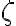 에 대해 실수,real_number 하나를 대응시키는 함수,function
에 대해 실수,real_number 하나를 대응시키는 함수,function ) 가 바로 확률변수이며
가 바로 확률변수이며
) 를 (줄여서) single letter
를 (줄여서) single letter  만으로도 자주 표기한다.
만으로도 자주 표기한다.
random variable
sample space
확률변수는 변수라기보다는 함수.
정의역이 표본공간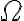 이고 치역이 실수집합의 부분집합인 함수.
이고 치역이 실수집합의 부분집합인 함수.
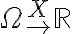
표본공간의 각 원소에 하나의 실수를 대응시키는 함수.
정의역이 표본공간
//mathworld
확률공간,probability_space에서 가측공간,measurable_space(AKA 상태공간,state_space)으로 가는 가측함수,measurable_function.
확률공간,probability_space에서 가측공간,measurable_space(AKA 상태공간,state_space)으로 가는 가측함수,measurable_function.
///wpko
확률변수의 정의역은 확률변수의 확률공간,probability_space.
확률변수의 공역은 확률변수의 상태공간,state_space.
만약 상태공간이 위상공간,topological_space인 경우, 상태공간은 통상적으로 보렐 시그마 대수(curr see 시그마대수,sigma-algebra)를 사용.
(반면, 보렐 시그마 대수 대신 르베그 가측집합의 시그마대수를 사용하면, 연속함수이지만 가측함수가 아닌 함수들이 존재하게 된다.)
확률변수의 정의역은 확률변수의 확률공간,probability_space.
확률변수의 공역은 확률변수의 상태공간,state_space.
만약 상태공간이 위상공간,topological_space인 경우, 상태공간은 통상적으로 보렐 시그마 대수(curr see 시그마대수,sigma-algebra)를 사용.
(반면, 보렐 시그마 대수 대신 르베그 가측집합의 시그마대수를 사용하면, 연속함수이지만 가측함수가 아닌 함수들이 존재하게 된다.)
Key Point. A random variable  is a function that maps each outcome
is a function that maps each outcome  of an experiment (e.g. a coin flip) to a number
of an experiment (e.g. a coin flip) to a number ,) which is the outcome value of
which is the outcome value of 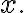
If the outcome value of is 1 then this may be written as
is 1 then this may be written as  or as
or as 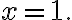
(Information Theory, Stone, p. 26)
If the outcome value of
(Information Theory, Stone, p. 26)
한국어 ‘확률’은 영어의 여러 단어 {probability(see 확률,probability), random, stochastic(see 확률과정,stochastic_process)}에 대응....
사건(event) =결과
표본공간(sample space): 모든 가능한 사건(event)의 집합
continuous random variable 연속확률변수
표본공간(sample space): 모든 가능한 사건(event)의 집합
continuous random variable 연속확률변수
RV가 가질 수 있는 값이 무한히 많음
discrete random variable 이산확률변수RV가 가질 수 있는 값이 가산,countable
mixed random variable// tmp from ![[https]](/123/imgs/https.png) 두산백과: pdf
두산백과: pdf
{
ALSOIN 확률밀도함수,probability_density_function,PDF
// 적분식 뒤에 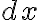 를 생략했네?
를 생략했네?
RV / distribution / function / 시각화
이산확률변수 ⇒ 이산확률분포 ⇒ 확률질량함수 ⇒ 이산확률분포표
연속확률변수 ⇒ 연속확률분포 ⇒ 확률밀도함수 ⇒ 확률밀도함수그래프
}
![[https]](/123/imgs/https.png) 두산백과: pdf
두산백과: pdf{
ALSOIN 확률밀도함수,probability_density_function,PDF
| 이산 RV | 연속 RV | |
| pmf의 자리? (설명에 그냥 확률 P를 씀) | pdf | |
| 평균,mean,average | ||
| 분산,variance |
RV / distribution / function / 시각화
이산확률변수 ⇒ 이산확률분포 ⇒ 확률질량함수 ⇒ 이산확률분포표
연속확률변수 ⇒ 연속확률분포 ⇒ 확률밀도함수 ⇒ 확률밀도함수그래프
}
Sub:
이산확률변수,discrete_random_variable
이항확률변수: see 이항분포,binomial_distribution
초기하확률변수: see 초기하분포,hypergeometric_distribution
기하확률변수: see 기하분포,geometric_distribution
벡터확률변수 vector random variable(셀 수 있는(countable) 확률 변수, 확률질량함수,probability_mass_function,PMF와 연관)
베르누이_확률변수,Bernoulli_random_variable
푸아송_확률변수,Poisson_random_variable
이항확률변수,binomial_random_variable
기하확률변수,geometric_random_variable
균등확률변수,uniform_random_variable
음이항확률변수,negative_binomial_random_variable
constant_random_variable
 Constant_random_variable redir. to:
Constant_random_variable redir. to:  Degenerate_distribution (on section 1)
Degenerate_distribution (on section 1)
Rel. 퇴화분포,degenerate_distribution
constant random variable
Up: 이산확률변수,discrete_random_variable
연속확률변수,continuous_random_variable 베르누이_확률변수,Bernoulli_random_variable
푸아송_확률변수,Poisson_random_variable
이항확률변수,binomial_random_variable
기하확률변수,geometric_random_variable
균등확률변수,uniform_random_variable
음이항확률변수,negative_binomial_random_variable
constant_random_variable
Rel. 퇴화분포,degenerate_distribution
constant random variable
Up: 이산확률변수,discrete_random_variable
이항확률변수: see 이항분포,binomial_distribution
초기하확률변수: see 초기하분포,hypergeometric_distribution
기하확률변수: see 기하분포,geometric_distribution
지시확률변수 indicator random variable
지시확률변수,indicator_random_variable
{
관심있는 어떤 사건,event이 있을 때, 사건이 일어나면 1, 안 일어나면 0인 확률변수.
사건,event A의 지시변수는, 사건 A가 일어나면 1, 일어나지 않으면 0으로 정의되는 확률변수.
지시확률변수,indicator_random_variable
{
관심있는 어떤 사건,event이 있을 때, 사건이 일어나면 1, 안 일어나면 0인 확률변수.
사건,event A의 지시변수는, 사건 A가 일어나면 1, 일어나지 않으면 0으로 정의되는 확률변수.
기호:
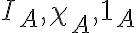
사건 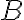 의 지시변수의 기대값,expected_value은 사건
의 지시변수의 기대값,expected_value은 사건 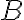 가 일어날 확률과 같음.
가 일어날 확률과 같음.
=\text{P}(B))
베르누이_확률변수,Bernoulli_random_variable와 same?? 차이가 있다면?
지시함수,indicator_function와 비슷한데?
IID,independent_and_identically_distributed
{
independent and identically distributed, i.i.d., iid
독립항등분포/독립동일분포/
{
independent and identically distributed, i.i.d., iid
독립항등분포/독립동일분포/
확률변수,random_variable 여러 개의 성질.
- 서로 독립이며,
- 동일한 확률분포,probability_distribution를 가질 때 iid라 함.
(정보이론)엔트로피,entropy 관련
(Cover Thomas p6)
고른분포,uniform_distribution와 iid의 관계 정확히? TBW.
1. 확률변수로 정의하는 사건 ¶
(Schaum's outline: Events defined by random variables)
page 10
확률변수 의 분포함수가
의 분포함수가 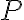 또는
또는 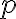 이다.
이다.
( 확률분포,probability_distribution가
연속분포일 때는 PDF) 이고, 이산분포일 때는 PMF
이고, 이산분포일 때는 PMF ) )
)
이 때 확률변수 의 기대값,expected_value 공식은
의 기대값,expected_value 공식은
![$E[X]=\sum_x xp(x)$ $E[X]=\sum_x xp(x)$](/123/cgi-bin/mimetex.cgi?\Large E[X]=\sum_x xp(x))
![$E[aX+b]=\sum_x (ax+b)p(x)$ $E[aX+b]=\sum_x (ax+b)p(x)$](/123/cgi-bin/mimetex.cgi?\Large E[aX+b]=\sum_x (ax+b)p(x))
![$E[f(X)]=\sum_x f(x)p(x)$ $E[f(X)]=\sum_x f(x)p(x)$](/123/cgi-bin/mimetex.cgi?\Large E[f(X)]=\sum_x f(x)p(x))
}
확률변수
( 확률분포,probability_distribution가
연속분포일 때는 PDF
이 때 확률변수
2. 확률변수의 독립 ¶
RV X, Y가 독립이기 위한 필요충분조건:
-∞ < x < ∞, -∞ < y < ∞ 에 대하여,
결합확률밀도함수,joint_probability_density_function,joint_PDF f:
=g_1(x)\cdot g_2(y))
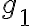 : x만의 음이 아닌 함수
: x만의 음이 아닌 함수
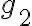 : y만의 음이 아닌 함수
: y만의 음이 아닌 함수
See also 독립성,independence#s-3결합확률밀도함수,joint_probability_density_function,joint_PDF f:
3. 확률변수의 기대값 ¶
// ㄷㄱㄱ
Expectation: a fixed value that represents the value of a random variable.
Expectation: a fixed value that represents the value of a random variable.
| 데이터 | 평균 |
| 확률변수 | 평균 = 기대값 |
확률변수의 경우 평균과 기대값이 같은 뜻이다. (둘 다 쓰인다)
확률변수의 평균을 기대값이라고 하는 것은 확률변수의 값을 실제로 (무작위로?) 관측해볼 때 '평균적으로 기대되는 값'이라는 의미이다.[1]
mklink 평균,mean,average
4. 확률변수의 표준화 ¶
확률변수 X에서 새로운 확률변수 Z를 만들어 내는 것.
방법은,
}{s(X)})
즉,
}X-\frac{E(X)}{s(x)})
여기에 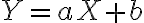 일 경우
일 경우 =E(aX+b)=aE(X)+b) 라는 사실을 적용하면,
라는 사실을 적용하면,
=\frac1{s(X)}E(X)-\frac{E(X)}{s(X)}=\frac{E(X)-E(X)}{s(X)}=0)
또한 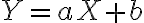 일 경우
일 경우 =a^2 V(X)) 이며
이며 =as(X)) 라는 사실 중 후자를 적용하면,
라는 사실 중 후자를 적용하면,
=\frac1{s(X)}s(X)=1)
즉 어떤 확률변수 X에 대해서도, 저 변환식으로 만든 새로운 확률변수 Z는, 반드시 평균이 0이고 표준편차가 1이 된다.
이것은 평균이 0이고 표준편차가 1인 확률변수에 대해서만 다양한 성질을 조사해두면 다른 모든 확률변수에 그 결과를 응용할 수 있다는 뜻이다.
방법은,
이것은 평균이 0이고 표준편차가 1인 확률변수에 대해서만 다양한 성질을 조사해두면 다른 모든 확률변수에 그 결과를 응용할 수 있다는 뜻이다.
(나가노 히로유키)
관련 내용 표준정규분포,standard_normal_distribution에서도 언급.
5. 확률변수의 합의 기대값(평균) ¶
확률변수  는
는 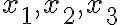 에서 어떤 값을 갖고
에서 어떤 값을 갖고
확률변수 는
는 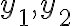 에서 어떤 값을 갖는다고 하자.
에서 어떤 값을 갖는다고 하자.
이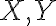 에 대해
에 대해
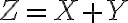
로 정의되는 새로운 확률변수 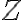 를 생각하기로 하자.
를 생각하기로 하자.
예를 들어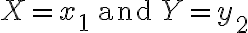 가 되는 확률을
가 되는 확률을 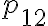 로 나타내기로 하면,
로 나타내기로 하면, 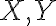 의 분포는 다음과 같이 2차원 표로 나타난다.
의 분포는 다음과 같이 2차원 표로 나타난다.
이와 같이 X와 Y의 확률분포를 한 표로 정리한 것을 확률변수 X와 Y의 동시분포(=결합확률분포,joint_probability_distribution?)라고 한다.
확률변수
이
예를 들어
| 계 | ||||
| 계 |
// 영어? mutually_disjoint? mutual_disjointness? mutually_exclusive? mutual_exclusion?(이건 mutex쪽이 생각나는데 아무튼) ....
같은 방식으로
X와 Y의 확률분포를 각각 따로 표로 만들면 다음과 같다.
E(X)=x1u1+x2u2+x3u3
E(Y)=y1v1+y2v2
이렇게 준비하고 E(Z)=E(X+Y)를 계산해보면
E(Z)=E(X+Y)
| X | x1 | x2 | x3 | 계 |
| 확률 | u1 | u2 | u3 | 1 |
| Y | y1 | y2 | 계 |
| 확률 | v1 | v2 | 1 |
이렇게 준비하고 E(Z)=E(X+Y)를 계산해보면
E(Z)=E(X+Y)
=(x1+y1)p11+(x2+y1)p21+(x3+y1)p31+(x1+y2)p12+(x2+y2)p22+(x3+y2)p32
=x1(p11+p12)+x2(p21+p22)+x3(p31+p32)+y1(p11+p21+p31)+y2(p12+p22+p32)
=x1u1+x2u2+x3u3 + y1v1+y2v2
=E(X)+E(Y)
따라서 E(X+Y)=E(X)+E(Y)인 것을 확인할 수 있다. //// del ok=x1(p11+p12)+x2(p21+p22)+x3(p31+p32)+y1(p11+p21+p31)+y2(p12+p22+p32)
=x1u1+x2u2+x3u3 + y1v1+y2v2
=E(X)+E(Y)
확률변수 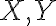 에 대해
에 대해
그리고 이 식의 성질을 되풀이해 사용하면 합의 기대값(평균)에 대해 일반적으로 다음 식이 성립한다.
확률변수 에 대해
에 대해
확률변수
(나가노 히로유키)
6. 확률변수의 곱의 기대값(평균) ¶
7. 확률변수의 합의 분산 ¶
이게 성립하는 건 확률변수가 서로 독립일 때만.
확률변수 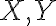 가 상호 독립일 때
가 상호 독립일 때
위 식의 성질을 되풀이해 사용하면
확률변수 이 상호 독립일 때
이 상호 독립일 때
확률변수
(나가노 히로유키)
8. Links ko ¶
수리통계학에서의 확률 변수와 확률 분포
https://freshrimpsushi.github.io/posts/random-variable-and-probability-distribution/
수리통계학에서의 랜덤 샘플 Random Sample
https://freshrimpsushi.github.io/posts/random-sample/
{
실현(realization), 샘플(sample), 랜덤 샘플의 정의. 사이트 참조.
https://freshrimpsushi.github.io/posts/random-variable-and-probability-distribution/
수리통계학에서의 랜덤 샘플 Random Sample
https://freshrimpsushi.github.io/posts/random-sample/
{
실현(realization), 샘플(sample), 랜덤 샘플의 정의. 사이트 참조.
확률 변수 X가 실제로 뽑힌 것을 실현(realization)이라 하고 보통 소문자 x로 나타냄.
실현이란 말을 쓰지 않더라도, 보통 convention은 대문자가 확률변수, 소문자가 데이터.
}
실현이란 말을 쓰지 않더라도, 보통 convention은 대문자가 확률변수, 소문자가 데이터.
}
9. etc ¶
LINKLATER:
 확률변수,RV
확률변수,RV
 Random_variable
Random_variable
![[https]](/123/imgs/https.png) 경제학사전: 확률변수
경제학사전: 확률변수
![[https]](/123/imgs/https.png) 수학백과: 확률변수
수학백과: 확률변수
 확률_변수
확률_변수
 Random_variable
Random_variable
https://mathworld.wolfram.com/RandomVariable.html
https://encyclopediaofmath.org/wiki/Random_variable
https://everything2.com/title/random variable
https://planetmath.org/randomvariable
분산,variance (확률변수가 하나일 때만?)
공분산,covariance (확률변수가 둘일 때만? - 복수인 경우는 다 여기 해당인듯.)
중심극한정리,central_limit_theorem,CLT
Twins:공분산,covariance (확률변수가 둘일 때만? - 복수인 경우는 다 여기 해당인듯.)
중심극한정리,central_limit_theorem,CLT
![[https]](/123/imgs/https.png) 경제학사전: 확률변수
경제학사전: 확률변수![[https]](/123/imgs/https.png) 수학백과: 확률변수
수학백과: 확률변수https://mathworld.wolfram.com/RandomVariable.html
https://encyclopediaofmath.org/wiki/Random_variable
https://everything2.com/title/random variable
https://planetmath.org/randomvariable
Up:
----
- [1] 통계가 빨라지는 수학력 p291


![[http]](/123/imgs/http.png)