MIT 18.02 Multivariable Calculus, Fall 2007
1. Lec 1 ¶
벡터,vector 내적,inner_product과 코사인법칙,cosines_law
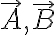 사이의 각이 θ이고
사이의 각이 θ이고
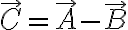 일 때,
일 때,
\cdot(\vec{A}-\vec{B}))
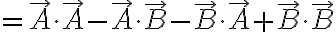
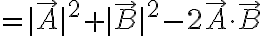
Sign of 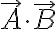 :
:
평면,plane 방정식
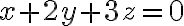
은, (계수를 보면)
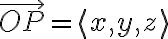 와
와 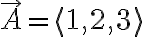
을 내적한
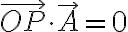 즉
즉 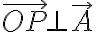
꼴이다.
pf.
평면,plane 방정식
Remember: 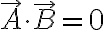
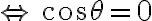
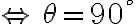
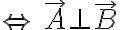
2. Lec 2 ¶
x방향으로  가 있고, 1사분면 적당한 방향으로
가 있고, 1사분면 적당한 방향으로  가 있고, y축 방향으로
가 있고, y축 방향으로 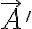 가 있는 그림. A, B 사잇각은 θ이고, B와 A' 사잇각은 θ'임.
가 있는 그림. A, B 사잇각은 θ이고, B와 A' 사잇각은 θ'임.
 를 90°만큼 돌린 것은
를 90°만큼 돌린 것은 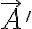
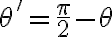
=\sin(\theta))

사인법칙 얘기
±(A와 B사이의 평행사변형의 넓이) =
)
±(삼각형의 넓이) =
)
따라서,
Determinant in space: 세 벡터.
=\begin{vmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{vmatrix})
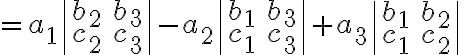
Geometrically,
Cross-product of 2 vectors in 3-space
Def.
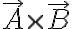 (is a vector)
(is a vector)
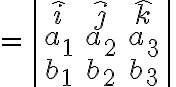
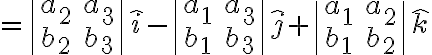
Thm.
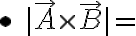 area of parallelogram
area of parallelogram
=) ⊥(parallel) to the plane of the parallelogram, with right-hand rule
⊥(parallel) to the plane of the parallelogram, with right-hand rule
Another look at volume
=\vec{A}\cdot(\vec{B}\times\vec{C})) 이다. 이유는?
이다. 이유는?

±(A와 B사이의 평행사변형의 넓이) =
Determinant in space: 세 벡터.
Cross-product of 2 vectors in 3-space
Def.

3. Lec 3 ¶


Matrices (행렬,matrix)
Often: linear relations(linear_relation - 선형관계,linear_relation) between variables
Ex: change of coordinate systems

Entries in matrix product AX: dot products between rows of A and columns of X
A: 3×3 matrix
X: column vector ↔ 3×1 matrix
Often: linear relations(linear_relation - 선형관계,linear_relation) between variables
Ex: change of coordinate systems

Entries in matrix product AX: dot products between rows of A and columns of X
A: 3×3 matrix
X: column vector ↔ 3×1 matrix

What AB represents: do transformation B, then transformation A.
(AB)X = A(BX)
(matrix product is associative)
Note: AB ≠ BA

Inverse matrix (역행렬,inverse_matrix)
Inverse of A: matrix M such that
Inverse of A: matrix M such that
AM = I
MA = I
Need: A square matrix n×nMA = I
M = A−1
Solution toAX = B
isX = A−1B
AX = B⇓
A−1(AX) = A−1B⇓
X = A−1BTODO: adjoint adjugate adjunct 차이?
Steps: (on a 3×3 example)
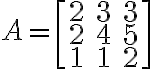
① Minors:
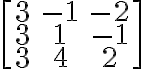
(예를 들어 위 행렬의 (1,1)의 3은 로 계산한 것.)
로 계산한 것.)
(예를 들어 위 행렬의 (1,1)의 3은
③ Transpose: switch rows and columns (전치,transposition or 전치,transpose... curr 전치행렬,transpose_matrix)
)
이것이 선형계,linear_system를 푸는 단계.
4. Lec 4 ¶
평면의 방정식
평면,plane
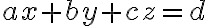
의 법선벡터,normal_vector는
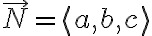
1) 원점을 지나고 법선벡터 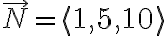 인 평면은?
인 평면은?
평면 위 점) 라 하면 (P is in plane)
라 하면 (P is in plane)
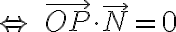

2) Plane through ) and
and 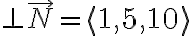
P is in plane
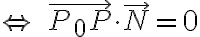

+5(y-1)+10(z+1)=0)
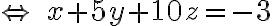
평면 위 점
P is in plane
6. Lec 6 ¶
Cycloid (wheel radius 1, at unit speed):
=\langle t-\sin t,1-\cos t\rangle)
Velocity vector:
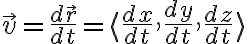
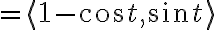
Speed(scalar):
^2+\sin^2 t})
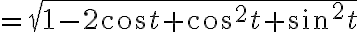
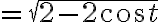
Acceleration(vector):
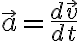
e.g. cycloid:
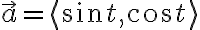
단위접벡터,unit_tangent_vector (See also 곡률,curvature)
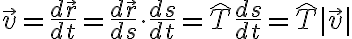
Velocity has
Velocity has
direction: tangent to trajectory 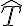
length: speed ds/dt
length: speed ds/dt
8. Lec 8 ¶
Function of 1 variable:
f(x)
ex. sin x
Function of 2 variables:ex. sin x
f(x, y)
ex. x² + y²
ex2. f(x,y)=1-x2-y2
contour_plot 얘기ex. x² + y²
ex2. f(x,y)=1-x2-y2
9. Lec 9 ¶
Approximation formula:
If we change
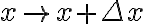
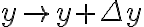
) then
then
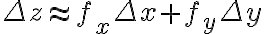
이 공식을 정당화하기 위해: 접평면,tangent_plane to ) 를 생각
를 생각
Know: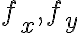 are 기울기,slopes of 2 접선,tangent_lines
are 기울기,slopes of 2 접선,tangent_lines
=a\;\Rightarrow\;L_1=\begin{cases}z=z_0+a(x-x_0)\\y=y_0\end{cases})
=b\;\Rightarrow\;L_2=\begin{cases}z=z_0+b(y-y_0)\\x=x_0\end{cases})
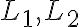 are both tangent to the graph
are both tangent to the graph .)
Together they determine a 평면,plane:
+b(y-y_0))
Approximation formula says: graph of  is close to its 접평면,tangent_plane.
is close to its 접평면,tangent_plane.
If we change
Know:
Together they determine a 평면,plane:
Ex. =x^2-2xy+3y^2+2x-2y)
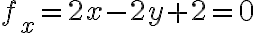
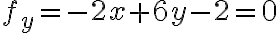
더하면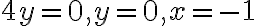 이렇게 1 critical point
이렇게 1 critical point =(-1,0))
더하면
Least-square interpolation //나중에 제곱,square>최소제곱,least_square 내삽,interpolation과 연결
Given experimental 자료,data:
 and
and 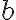
minimizing total square deviation
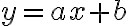
Deviation for each data point: (편차,deviation)
)
Minimize
![$D(a,b)=\sum_{i=1}^{n}\left[y_i-(ax_i+b)\right]^2$ $D(a,b)=\sum_{i=1}^{n}\left[y_i-(ax_i+b)\right]^2$](/123/cgi-bin/mimetex.cgi?\Large D(a,b)=\sum_{i=1}^{n}\left[y_i-(ax_i+b)\right]^2)
편미분하면,
)\cdot(-x_i)=0)
)\cdot(-1)=0)
=0\\ \sum_{i=1}^{n}(x_ia+b-y_i)=0\end{cases})
a+\left(\sum_{i=1}^{n}x_i\right)b=\sum_{i=1}^{n}x_iy_i\\\left(\sum_{i=1}^{n}x_i\right)a+nb=\sum_{i=1}^{n}y_i\end{cases})
2×2 linear system, solve for (a, b)
Given experimental 자료,data:
(x1, y1), (x2, y2) … (xn, yn)
Find best fit line - best minimizing total square deviation
2×2 linear system, solve for (a, b)


