Contents
- 1. Lec 1
- 2. Lec 2
- 3. Lec 3
- 4. Lec 4
- 5. Lec 5
- 6. Lec 6
- 7. Lec 7
- 8. Lec 8
- 9. Lec 9
- 10. Lec 10
- 11. Lec 11
- 12. Lec 12
- 13. Lec 13
- 14. Lec 14
- 15. Lec 15
- 16. Lec 16
- 17. Lec 17
- 18. Lec 18
- 19. Lec 19
- 20. Lec 20
- 21. Lec 21
- 22. Lec 22
- 23. Lec 23
- 24. Lec 24
- 25. Lec 25
- 26. Lec 26
- 27. Lec 27
- 28. Lec 28
- 29. Lec 29
- 30. Lec 30
- 31. Lec 31
- 32. Lec 32
- 33. Lec 33
- 34. Lec 34
- 35. Lec 35
- 36. Lec 36
- 37. Lec 37
- 38. Lec 38
- 39. Lec 39
2. Lec 2 ¶
average change = 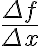
instantaneous rate =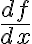
Examples
=f(x_0))
Jump discontinuity
instantaneous rate =
Examples
- q = charge, dq/dt = current
- s = distance, ds/dt = speed
- T = temperature, dT/dx = temperature gradient
- sensitivity of measurements
: 좌극한과 우극한이 존재하나 다름.
Removable discontinuity: 좌극한과 우극한이 같고 함수값만 동떨어져 있음.
Infinite discontinuityEx. 1/x 쌍곡선,hyperbola : ±∞
// (이상 몇가지 불연속성,discontinuity)Proof of -f(x_0)=0)
-f(x_0)}{x-x_0}(x-x_0)=f%27(x_0)\cdot0=0 \rule{10}{10})
4. Lec 4 ¶
Product rule 증명은 생략

Quotient rule 증명생략
%27=\frac{u%27v-uv%27}{v^2})
Composition rule
Higher derivative의 notation (u(n), dn/dxn u, Dnu...)
Ex. Dnxn = ?
Dxn = nxn-1
D2xn = n (n-1) xn-2
D3xn = n (n-1) (n-2) xn-3
SoD2xn = n (n-1) xn-2
D3xn = n (n-1) (n-2) xn-3
...
Dn-1xn = n (n-1) … x15. Lec 5 ¶
Implicit differentiation
지금까지
양변을 미분하면 (좌변에 chain rule 적용된 것임)
Example 3:
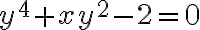
explicit하게 하면
quadratic_formula를 쓰면
}}{2})
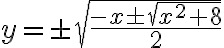
explicit하게 하면
quadratic_formula를 쓰면
implicit하게 하면
-0=0)
y%27=-y^2)

9. Lec 9 ¶
Applications of differentiation
i.e.
Curve)
+f%27(x_0)(x-x_0)) tangent line.
tangent line.
Ex.
f(x)=ln x, f'(x)=1/x
=\ln1=0,\;f%27(1)=1)
)
So,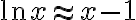 (x가 1 근방일때)
(x가 1 근방일때)
Curve
f(x)=ln x, f'(x)=1/x
So,
x0=0이면
\approx f(0)+f%27(0)x)
따라서 (x0 ≈ 0)일 때는
sin x ≈ x
cos x ≈ 1
exp x ≈ 1 + x
ln(1 + x) ≈ x
(1 + x)r ≈ 1 + rx
이상 ≈의 좌변은 hard function, 우변은 easy function임을 볼 수 있음cos x ≈ 1
exp x ≈ 1 + x
ln(1 + x) ≈ x
(1 + x)r ≈ 1 + rx
Ex 2.
ln(1.1) ≈ 1/10
∵ ln(1+x) ≈ x, x=1/10
ln(1.1) ≈ 1/10
∵ ln(1+x) ≈ x, x=1/10
Ex 3.
Find linear approx near x=0 (x≈0) of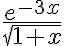
^{-1/2})
\left(1-\frac12x\right))

drop x2 terms (negligible)
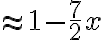
Ex 4. (real life)
생략
Find linear approx near x=0 (x≈0) of
생략
10. Lec 10 ¶
Quadratic approximation
(use these when linear is not enough)
(use these when linear is not enough)
x가 0에 가까울 때 다음 관계도 성립
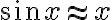
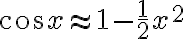
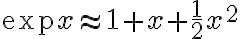
\approx x-\frac12 x^2)
^r\approx 1+rx+\frac{r(r-1)}{2}x^2)
21. Lec 21 ¶
로그,log의 적분을 쓴 정의
...
다음 함수를 오래 설명
=\int_0^x e^{-t^2}dt)
=e^{-x^2})
=-2xe^{-x^2})
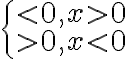 이며 기함수 즉 F(-x)=-F(x)
이며 기함수 즉 F(-x)=-F(x)
여기서 오차함수,error_function (curr. goto 함수,function#s-17) 이 나옴
=\frac{2}{\sqrt{\pi}}\int_0^xe^{-t^2}dt=\frac{2}{\sqrt{\pi}}F(x))
그래프: arctan 유사한 모양, horizontal asymptote는 =\frac{\sqrt{\pi}}{2},\; \lim_{x\to-\infty}F(x)=-\frac{\sqrt{\pi}}{2})
그래프 : 정규분포 모양
그리고 다음을 Fresnel integral 이라 함
=\int_0^x\cos(t^2)dt)
=\int_0^x\sin(t^2)dt)
...
곡선 사이의 면적을 구하는 것 설명
22. Lec 22 ¶
얇게 잘라 부피를 구하는 것을 설명 (volumes by slicing)
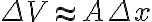 (one slice)
(one slice)
dx)
dx)
회전해서 생긴 부피 설명 (solids of revolution)
35. Lec 35 ¶
극한이 부정형,indeterminate_form일 때 활용하는
로피탈_정리,L_Hopital_s_rule
로피탈_정리,L_Hopital_s_rule
Version 1
}{g(x)}=\lim_{x\to a}\frac{f%27(x)}{g%27(x)})
provided=g(a)=0)
and the right-hand limit exists.
provided
and the right-hand limit exists.
36. Lec 36 ¶
Def:
dx=\lim_{N\to\infty}\int_a^Nf(x)dx)
The integral converges if limit exists; diverges if not.
Example:
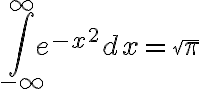
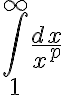 diverges if
diverges if 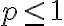
The integral converges if limit exists; diverges if not.
이건 판정법 내용인가?
Limit comparison
If\sim g(x)) (similar) as
(similar) as 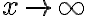
dx\;\textrm{and}\;\int_a^{\infty}g(x)dx) either both converge or both diverge.
either both converge or both diverge.
If
(f~g as x→∞ means f(x)/g(x)→1)
then Ex.
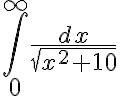
 이므로
이므로
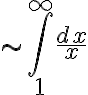
- diverges.
Ex.
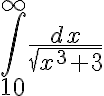
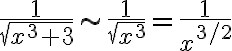
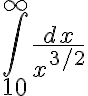
- convergent.
37. Lec 37 ¶
Improper integrals (2nd kind)
기하급수,geometric_series
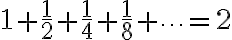
)
이 식은
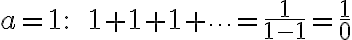 diverges
diverges
}=\frac12) - 좌변 diverges (틀림)
- 좌변 diverges (틀림)
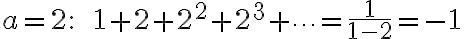 - 좌변 diverges (clearly wrong)
- 좌변 diverges (clearly wrong)
Notation
Ex 1.
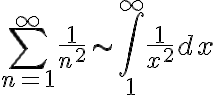 convergent
convergent
LHS: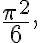 RHS: 1
RHS: 1
Ex 1.
LHS:
Ex 3.
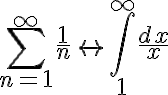 diverges
diverges
인데
Integral Comparison
If ) is decreasing,
is decreasing, >0,) then
then
 - \int_1^{\infty} f(x)dx \right| < f(1))
and
) and
and dx)
converge or diverge together.
(rel. 적분판정법,integral_test)
Limit Comparison
If
\sim g(n) \left(\text{ (i.e. } \frac{f(n)}{g(n)}\to 1\text{ as } n\to\infty \right))
and>0 \; \forall n ) then,
then,
,\,\sum g(n)) either both converge or both diverge.
either both converge or both diverge.
and
Ex.
 diverges.
diverges.
Ex.
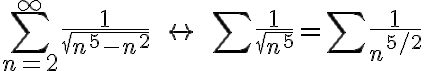 converges.
converges.
38. Lec 38 ¶
(김홍종 미적분학 1+에도 언급된 '블럭을 쌓아 한강을 건널 수 있는가?' 그 문제)
도중에 greedy_algorithm 언급
결론은 가능하다는 것. 다만 앞의 테이블을 건너려면 달의 거리의 두 배만큼의 높이를 쌓아야 함.
도중에 greedy_algorithm 언급
결론은 가능하다는 것. 다만 앞의 테이블을 건너려면 달의 거리의 두 배만큼의 높이를 쌓아야 함.
Power Series (멱급수,power_series)
양변에
위 두 식에 대해, 위 식에서 아래 식을 빼면
Reasoning (is) incomplete because it requires  exist.
exist.
e.g.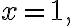
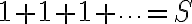

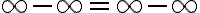
e.g.
General Power Series (멱급수,power_series)
그래서 우린 수렴반지름 안에서만 머무를 것이다.
(R 안에 있을 때는 0으로 매우 빠르게 접근하지만)
(R 밖에 있을 때는 0으로 가지도 않는다)
이건 모든 멱급수(power series)에 적용된다.
Rules for convergent power series are just like polynomials.
+g(x),\;f(x)g(x),\;f(g(x)),\;\frac{f(x)}{g(x)},\;\frac{d}{dx}f(x),\;\int f(x)dx)

