Contents
- 1. Physics KPOPE
- 2. network theory
- 3. 3Blue1Brown series: Essence of calculus 시청 기록
- 4. 물성전자
- 5. 전자기학 세종대 서용호
- 6. 천문학,astronomy
- 7. 허블 법칙
- 8. 우주의 나이 구하기
- 9. mind, mental, brain, study, memory, thinking, intelligence, ..관련
- 10. AI, ML, NN, ... 관련
- 11. rest
- 12. Excerpt 1 - 통계, 모멘트
- 13. Excerpt 2 - 확률분포
- 14. 인용
- 15. Cmts
1.1. M1 ¶
물리에서 회전,rotation 시 벡터,vector: 규칙성을 가지고 그 성분이 변화하는 것.
더 응용하면 cross product가 관여하는 torque, angular momentum 등은 동일한 rotational property를 가지고 있지만, 일반 벡터와 parity가 서로 다르게 된다.
벡터는 x에 -x를 집어넣으면 원점대칭하면 부호가 바뀌는데,
axial_vector라고 얘기하는 cross product 로 연결된 벡터는 뒤집어도 부호가 바뀌지 않는다.
마찬가지로 스칼라,scalar도 회전에 대해 바뀌지 않지만
더 응용하면 cross product가 관여하는 torque, angular momentum 등은 동일한 rotational property를 가지고 있지만, 일반 벡터와 parity가 서로 다르게 된다.
벡터는 x에 -x를 집어넣으면 원점대칭하면 부호가 바뀌는데,
axial_vector라고 얘기하는 cross product 로 연결된 벡터는 뒤집어도 부호가 바뀌지 않는다.
마찬가지로 스칼라,scalar도 회전에 대해 바뀌지 않지만
그냥 scalar인 것이 있고
parity에 대해 부호가 바뀌는 scalar가 있는데 이걸 유사스칼라,pseudoscalar { pagename via pseudoscalar /
pseudoscalar /  pseudoscalar
pseudoscalar  pseudoscalar }라고 하고, 그 대표적인 예는
pseudoscalar }라고 하고, 그 대표적인 예는  triple scalar product가 있다. (스칼라삼중곱,scalar_triple_product? curr 삼중곱,triple_product)
triple scalar product가 있다. (스칼라삼중곱,scalar_triple_product? curr 삼중곱,triple_product)
(KU이정일 M1 1m)parity에 대해 부호가 바뀌는 scalar가 있는데 이걸 유사스칼라,pseudoscalar { pagename via
(선형독립,linear_independence)
Any two vectors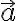 and
and 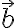 are linearly independent when
are linearly independent when
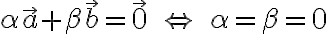
이건 i.e. 두 벡터가 한 직선 위에 있지 않다, i.e. 두 벡터로 한 평면을 만들 수 있다는 것.
 개의 linearly independent vectors를 모아 놓으면,
개의 linearly independent vectors를 모아 놓으면,  차원 유클리드_공간,Euclidean_space을 span할 수 있는 basis를 가지게 될 수 있다.
차원 유클리드_공간,Euclidean_space을 span할 수 있는 basis를 가지게 될 수 있다.
Any two vectors
1.2. tmpx ¶
(그렇다면 성질은) 이것들은 서로 직교한다(직교성,orthogonality). The Cartesian basis vectors are orthogonal:

여기서 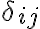 는 크로네커_델타,Kronecker_delta. (index가 서로 같으면 하나,one, 서로 다르면 영,zero.)
는 크로네커_델타,Kronecker_delta. (index가 서로 같으면 하나,one, 서로 다르면 영,zero.)
2.1. centrality ¶
번역:
중심성 (커뮤니케이션 연구를..)
중심성 (커뮤니케이션 연구를..)
// from https://process-mining.tistory.com/35 (short)
node의 중요성을 나타내는 centrality의 종류. 세가지만 알아보면
degree_centrality - simple
closeness_centrality
1 / (해당 노드에 대한, 모든 노드의 shortest_path 의 합)
아이디어: 중요한 노드일수록 다른 노드로 가는 경로가 짧을 것이다
betweenness_centrality아이디어: 중요한 노드일수록 다른 노드로 가는 경로가 짧을 것이다
모든 두 노드 사이의 shortest_path가 해당 노드를 지나가는 수
degree_centrality
degree centrality 연결정도 중심성 : node가 다른 node들과 얼마나 많이 연결되었는가를 표현.
closeness centrality 근접 중심성 : 노드가 다른 노드들과 얼마나 가까이 있는가를 나타냄.
다른 노드들과의 거리,distance(두 점을 연결하는 가장 짧은 경로,path ‘의 길이,length’란 말이 생략된 듯)의 합,sum이 작을수록 근접 중심성이 높다.
i.e. 네트워크를 통해 전달되는 정보, 자원 등이 특정 노드까지 도착하는 데 걸리는 시간이 작을수록 근접 중심성이 높다고 할 수 있다.
betweenness centrality 매개 중심성 : 특정 노드가 서로 다른 두 노드 간의 최단경로(geodesic path)에 얼마나 자주 위치하는가를 의미.
매개 중심성이 높을수록 해당 네트워크에서 다리와 같은 역할을 담당.
중개자나 gatekeeper나 정보 여과자 기능을 할 수 있음.
degree centrality 연결정도 중심성 : node가 다른 node들과 얼마나 많이 연결되었는가를 표현.
in-degree centrality 내향 연결정도 중심성 : 크면 '인기가 많다'
out-degree centrality 외향 연결정도 중심성 : 크면 '영향력이 크다'
in-degree centrality가 크고, out-degree centrality가 0에 가까우면 sink라고 부른다.
in-degree centrality가 0에 가깝고, out-degree centrality가 크면 source라고 부른다.
closeness_centrality out-degree centrality 외향 연결정도 중심성 : 크면 '영향력이 크다'
in-degree centrality가 크고, out-degree centrality가 0에 가까우면 sink라고 부른다.
in-degree centrality가 0에 가깝고, out-degree centrality가 크면 source라고 부른다.
closeness centrality 근접 중심성 : 노드가 다른 노드들과 얼마나 가까이 있는가를 나타냄.
다른 노드들과의 거리,distance(두 점을 연결하는 가장 짧은 경로,path ‘의 길이,length’란 말이 생략된 듯)의 합,sum이 작을수록 근접 중심성이 높다.
i.e. 네트워크를 통해 전달되는 정보, 자원 등이 특정 노드까지 도착하는 데 걸리는 시간이 작을수록 근접 중심성이 높다고 할 수 있다.
방향성 있는 네트워크에서
in-closeness centrality 내향 근접 중심성 : 높으면 네트워크 내의 통합에 기여한다고 볼 수 있다
out-closeness centrality 외향 근접 중심성 : 높으면 네트워크 내에서 정보, 자원 등의 신속한 전달에 기여한다고 할 수 있다
betweenness_centralityin-closeness centrality 내향 근접 중심성 : 높으면 네트워크 내의 통합에 기여한다고 볼 수 있다
out-closeness centrality 외향 근접 중심성 : 높으면 네트워크 내에서 정보, 자원 등의 신속한 전달에 기여한다고 할 수 있다
betweenness centrality 매개 중심성 : 특정 노드가 서로 다른 두 노드 간의 최단경로(geodesic path)에 얼마나 자주 위치하는가를 의미.
매개 중심성이 높을수록 해당 네트워크에서 다리와 같은 역할을 담당.
중개자나 gatekeeper나 정보 여과자 기능을 할 수 있음.
eigenvector_centrality
eigenvector centrality 아이겐벡터 중심성 고유벡터 중심성이라고 하는게 낫지 않을지? - 고유벡터,eigenvector
특정 노드와 직접 연결되어 있는 다른 노드들의 중심성 값의 합에 비례하여 결정됨.
eigenvector centrality 아이겐벡터 중심성 고유벡터 중심성이라고 하는게 낫지 않을지? - 고유벡터,eigenvector
특정 노드와 직접 연결되어 있는 다른 노드들의 중심성 값의 합에 비례하여 결정됨.
beta_centrality
beta centrality 베타 중심성
연결정도 중심성과 아이겐벡터 중심성을 모두 포괄.
β=0 이면 연결정도 중심성 값과 일치.
β의 절대값이 아이겐값 최고치의 역수에 가까우면 아이겐벡터 중심성 값과 거의 일치.
β가 0에 가까울수록 중심성 분석에 있어서 짧은 경로만을 중요하게 간주함을 뜻함.
β값이 아이겐값 최고치의 역수에 가까울수록 긴 경로도 중요하게 생각함을 의미.
β값이 음수이면, 연결관계가 많은 노드들과 연결되어 있는 것보다 연결관계가 적은 노드들과 연결되어 있는 것이 해당 노드가 그 네트워크에서 파워를 확보하기가 용이한 경우가 이에 해당함.
beta centrality 베타 중심성
연결정도 중심성과 아이겐벡터 중심성을 모두 포괄.
β=0 이면 연결정도 중심성 값과 일치.
β의 절대값이 아이겐값 최고치의 역수에 가까우면 아이겐벡터 중심성 값과 거의 일치.
β가 0에 가까울수록 중심성 분석에 있어서 짧은 경로만을 중요하게 간주함을 뜻함.
β값이 아이겐값 최고치의 역수에 가까울수록 긴 경로도 중요하게 생각함을 의미.
β값이 음수이면, 연결관계가 많은 노드들과 연결되어 있는 것보다 연결관계가 적은 노드들과 연결되어 있는 것이 해당 노드가 그 네트워크에서 파워를 확보하기가 용이한 경우가 이에 해당함.
(커뮤니케이션 연구를 위한 네트워크 분석)
참고 사이트
bmks ko
https://bab2min.tistory.com/554 요약
{
Source: Zafarani (Zafarani, R., Abbash, M.A., & Liu, H, 2014, Social Media Mining : An introduction 의 3.1장)
bmks ko
https://bab2min.tistory.com/554 요약
{
Source: Zafarani (Zafarani, R., Abbash, M.A., & Liu, H, 2014, Social Media Mining : An introduction 의 3.1장)
차례로,
연결중심성 degree_centrality Cd
가장 간단. node의 모든 edge의 수 (weighted graph의 경우 모든 weight의 합)으로 평가.
정규화,normalization하기도 함. 그 방법은
고유벡터중심성 eigenvector_centrality Ce
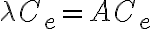
여기서
 : adjacency_matrix
: adjacency_matrix
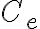 : centrality를 나타내는 열벡터
: centrality를 나타내는 열벡터
근데 Ce의 한계는 DAG같은 경우 중심성이 0으로 나오는 경우가 있다는 것. 이걸 방지하기 위해 모든 노드의 중심성에 특정한 상수값을 더하는 방식을 Katz가 제안
Katz 중심성 Katz_centrality Ck
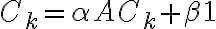 (1은 모든 성분이 1인 1×n 행렬)
(1은 모든 성분이 1인 1×n 행렬)
그리고 그것을 개선한 게 페이지랭크. Ck에서는 한 노드의 중요성이(∝중심성?) 연결된 다른 노드까지 전파되는 특징이 있다. 그래서 out edge로 영향력이 지나치게 퍼지는 것을 막은 것이 pagerank.
페이지랭크,PageRank Cp
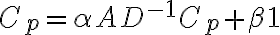
여기서
이상 살펴본 4가지 centrality는 한 node가 다른 node와 얼마나 연결되어있는지를 중요성의 기준으로 삼은 것인데, 그렇지 않는 measure도 있다.
가장 간단. node의 모든 edge의 수 (weighted graph의 경우 모든 weight의 합)으로 평가.
정규화,normalization하기도 함. 그 방법은
- 가능한 최대 Cd값인
로 나누기
- 그 네트워크의 가장 큰 Cd값으로 나누기
- 네트워크 내 모든 Cd값의 합으로 나누기
고유벡터중심성 eigenvector_centrality Ce
Katz 중심성 Katz_centrality Ck
페이지랭크,PageRank Cp
이상 살펴본 4가지 centrality는 한 node가 다른 node와 얼마나 연결되어있는지를 중요성의 기준으로 삼은 것인데, 그렇지 않는 measure도 있다.
매개 중심성 betweenness_centrality Cb
"A도시의 중심성을 보려면, A를 제외한 도시들에 사는 사람들이 다른 도시로 이동할 때 A를 얼마나 많이 거쳐가는가를 보면 된다"
i.e.
node A의 중요성은, X, Y(X∉A, Y∉B)에 대해 X-Y의 최단경로,shortest_path에 A가 포함된 비율로 볼 수 있다.
그래서 A를 항상 거쳐간다면 1.
A를 전혀 거치지 않는다면 0.
이것을 A를 제외한 모든 node들에 대해 계산하여 합하면 Cb.
정규화,normalization한다면 방법은
더 중요한 노드일수록 다른 노드까지 도달하는 경로,path가 짧을 것이라는 가정을 한 것.
방법은 자기를 제외한 다른 노드들까지의 최단경로,shortest_path 길이,length들의 평균의 역수를 구하는 것.
 = \frac1{ \frac1{N-1}\sum_{X\ne A} l_{X,A}} = \frac{N-1}{\sum_{X\ne A}l_{X,A}})
(여기서 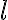 은 노드 사이의 최단거리)
은 노드 사이의 최단거리)
"A도시의 중심성을 보려면, A를 제외한 도시들에 사는 사람들이 다른 도시로 이동할 때 A를 얼마나 많이 거쳐가는가를 보면 된다"
i.e.
node A의 중요성은, X, Y(X∉A, Y∉B)에 대해 X-Y의 최단경로,shortest_path에 A가 포함된 비율로 볼 수 있다.
그래서 A를 항상 거쳐간다면 1.
A를 전혀 거치지 않는다면 0.
이것을 A를 제외한 모든 node들에 대해 계산하여 합하면 Cb.
정규화,normalization한다면 방법은
가능한 최대의 Cb값으로 나누기
근접 중심성 closeness_centrality Ccex. 전체 node수가 N이라면, A를 제외한 노드 수는 N-1이고, 그 중에 순서 없이 둘을 뽑는 경우가 (N-1)*(N-2)/2이고, 이게 모두 1이 나오는 게 최대값이므로, 노드개수가 N인 네트워크의 최대 Cb는 (N-1)*(N-2)/2 이다. 이걸로 나누는 게 정규화.
더 중요한 노드일수록 다른 노드까지 도달하는 경로,path가 짧을 것이라는 가정을 한 것.
방법은 자기를 제외한 다른 노드들까지의 최단경로,shortest_path 길이,length들의 평균의 역수를 구하는 것.
조화 중심성 harmony_centrality Ch
harmonic_centrality?
=\frac1{N-1}\sum_{X\ne A}\frac1{l_{X,A}})
경로가 존재하지 않을 경우 최단거리를 무한대로 보고 최단거리의 역수는 0으로 생각.
harmonic_centrality?
3.1. Chap 1 ¶
https://www.youtube.com/watch?v=WUvTyaaNkzM
소개에 나오는 몇 식들
=f\,dg+g\,df)
=\int_0^x \frac{dF}{dg}(t)dt)
=\sum_{n=0}^{\infty}f^{(n)}(a)\frac{(x-a)^n}{n!})
예: 원의 넓이 구하기.
반지름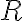 인 원의 넓이는 왜
인 원의 넓이는 왜 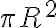 인가?
인가?
이것은 integrals(I), derivatives(D), 그리고 이 둘이 서로 반대라는 것과 관련.
)
넓이를 구하기 위해 작게 잘라 합치는 것을 생각.
동심원을 따라 자른 고리(concentric rings)로 자르는 방법.
그래서, 중심에서 거리가 인 고리의 넓이는?
인 고리의 넓이는?
펴면 긴 직사각형이 된다고 생각하면(rectangle-ish),
직사각형의 길이는 원의 둘레인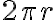 인데,
인데,
직사각형의 얇은 너비(두께)는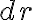 로 나타낸다.
로 나타낸다.
그래서 고리의 넓이는 대략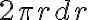 이다.
이다.
정확하지 않다고 해도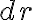 이 0으로 갈수록 정확해질 것이다.
이 0으로 갈수록 정확해질 것이다.
근사,approximation이지만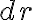 이 0으로 갈수록 오차,error가 줄어든다.
이 0으로 갈수록 오차,error가 줄어든다.
그리하여 이 직사각형들을 가로 축 위에 짧은 것부터 늘어놓으면 기울기
축 위에 짧은 것부터 늘어놓으면 기울기 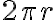 인 직선이 나오고 그 밑의 면적이 원의 면적과 같으며, 1/2 × (가로) × (높이)는
인 직선이 나오고 그 밑의 면적이 원의 면적과 같으며, 1/2 × (가로) × (높이)는
(2\pi R)=\pi R^2)
이 된다.
소개에 나오는 몇 식들
반지름
이것은 integrals(I), derivatives(D), 그리고 이 둘이 서로 반대라는 것과 관련.
동심원을 따라 자른 고리(concentric rings)로 자르는 방법.
그래서, 중심에서 거리가
펴면 긴 직사각형이 된다고 생각하면(rectangle-ish),
직사각형의 길이는 원의 둘레인
직사각형의 얇은 너비(두께)는
그래서 고리의 넓이는 대략
정확하지 않다고 해도
근사,approximation이지만
그리하여 이 직사각형들을 가로
그렇다면 삼각형 넓이 구하는 법을 쓸 수 없는 포물선 아래 넓이 구하기는?
이것은 integral of) 이다.
이다.
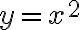 에서
에서  가 0~3 까지의 넓이를 구한다면
가 0~3 까지의 넓이를 구한다면
가로 폭이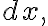 세로 높이가
세로 높이가 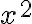 인 가느다란 직사각형의 넓이는
인 가느다란 직사각형의 넓이는 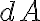 (difference in Area)
(difference in Area)
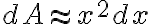
(여기서도 역시 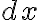 가 작아질수록 참값에 가까워진다.)
가 작아질수록 참값에 가까워진다.)
이것을 재배열(rearrange)하면
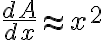
 가 3 근처일 때,
가 3 근처일 때,
-A(3)}{0.001}\approx 3^2)
이것은 3 근처 뿐 아니라 다른  에서도 성립한다.
에서도 성립한다.
일반적으로
dx)
)
좌변을 "derivative" of A라고 하며, 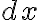 가 0으로 갈수록 정확해진다.
가 0으로 갈수록 정확해진다.
이것은 integral of
가로 폭이
이것을 재배열(rearrange)하면
일반적으로
3.2. Chap 2 The paradox of the derivative ¶
https://www.youtube.com/watch?v=9vKqVkMQHKk
목표: 1) 도함수(미분,derivative)에 대해 배우고, 2) 모순을 피하기.
보통 도함수는 "instantaneous rate of change"를 구하는 것이라 말한다.
그런데 oxymoron(
oxymoron( 모순어법)이 있는 게,
모순어법)이 있는 게,
velocity = (change in distance) / (change in time)
목표: 1) 도함수(미분,derivative)에 대해 배우고, 2) 모순을 피하기.
보통 도함수는 "instantaneous rate of change"를 구하는 것이라 말한다.
그런데
instantaneous: one point in time
change: requires multiple points in time
이동하는 물체의change: requires multiple points in time
거리를 ) 로
로
속도를) 로 표기.
로 표기.
속도 = (거리 변화) / (시간 변화)속도를
velocity = (change in distance) / (change in time)
순간(moment, 특정 시점)의 속도(velocity)를 구하는 것이 가능한가? 속도에는 두 시점이 필요하지 않은가? 이것이 이상하게 느껴지면 잘 하고 있는 것이며, 이건 미적분의 아버지들이 했던 고민이기도 하다.
시각=3s에서 거리=20m
시각=3.01s에서 거리=20.21m
라면, 위 식에 의해 속도는
{\rm m}}{(3.01-3){\rm s}})
짧은 시간 구간, 예를 들어 0.01초를 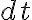 라고 하자. 또, 그 짧은 시간동안 움직인 거리를
라고 하자. 또, 그 짧은 시간동안 움직인 거리를 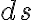 라고 하자.
라고 하자.
{\rm m}}{(\underbrace{3.01-3}_{dt}){\rm s}})
그래서 (매우 작은tiny 거리) / (매우 작은 시간) 비는 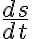 이다.
이다.
=\frac{s(t+dt)-s(t)}{dt})
이런 ds/dt라는 생각, 즉 (매우 작은 dt)동안 발생하는 (ds만큼의 작은 차이)라는 생각은 미분이 무엇인가라는 물음에 거의 답한 것이다.
어떤 특정한 dt에 대해, ds/dt는 두 점을 통과하는 직선의 기울기,slope.
dt가 0에 접근하고, 두 점이 서로 가까워지면서 접선의 기울기와 동일해진다.
dt가 무한히 작다는 말은 아니다. (dt is not "infinitely small")
0이라는 말도 아니다. (dt is not 0)
유한히 작으면서 0이 아닌 값이다. 0에 접근할 뿐이다.
앞서 말한 instantaneous rate of change보다는 best constant approximation around a point라고 생각하는 게 편하다.
(dt를 하나의 수 처럼 생각하고 식을 풀어 dt→0일 때 dt가 곱해지는 항을 모두 소거하는 방법을 설명)
하지만 이렇게 대수적으로(algebraically) 항상 식을 풀어야 하는 것은 아니다.
시각=3.01s에서 거리=20.21m
라면, 위 식에 의해 속도는
어떤 특정한 dt에 대해, ds/dt는 두 점을 통과하는 직선의 기울기,slope.
dt가 0에 접근하고, 두 점이 서로 가까워지면서 접선의 기울기와 동일해진다.
dt가 무한히 작다는 말은 아니다. (dt is not "infinitely small")
0이라는 말도 아니다. (dt is not 0)
유한히 작으면서 0이 아닌 값이다. 0에 접근할 뿐이다.
앞서 말한 instantaneous rate of change보다는 best constant approximation around a point라고 생각하는 게 편하다.
(dt를 하나의 수 처럼 생각하고 식을 풀어 dt→0일 때 dt가 곱해지는 항을 모두 소거하는 방법을 설명)
하지만 이렇게 대수적으로(algebraically) 항상 식을 풀어야 하는 것은 아니다.
도함수는 본질적으로 모순적인 문구인 "순간변화율(instantaneous rate of change)" 보다는 "변화율에 대한 가장 좋은 상수 근사값(best constant approximation for rate of change)"라고 생각하는 게 좋다.
3.3. Chap 3 Derivative formulas through geometry ¶
https://www.youtube.com/watch?v=S0_qX4VJhMQ
Tiny nudges 언급.
정사각형이 오른쪽으로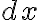 만큼, 아래쪽으로도
만큼, 아래쪽으로도 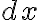 만큼 늘어나서 4개의 직사각형이 생긴 상황.
만큼 늘어나서 4개의 직사각형이 생긴 상황.
=x^2)
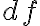 는 (길고 가는 직사각형 두개) + (아주 작은 정사각형)이므로,
는 (길고 가는 직사각형 두개) + (아주 작은 정사각형)이므로,
^2)
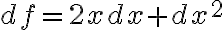
여기서 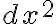 는 tiny change squared: negligible(safe to ignore).
는 tiny change squared: negligible(safe to ignore).
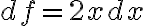
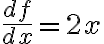
Tiny nudges 언급.
정사각형이 오른쪽으로
Contents
- 1. Physics KPOPE
- 2. network theory
- 3. 3Blue1Brown series: Essence of calculus 시청 기록
- 4. 물성전자
- 5. 전자기학 세종대 서용호
- 6. 천문학,astronomy
- 7. 허블 법칙
- 8. 우주의 나이 구하기
- 9. mind, mental, brain, study, memory, thinking, intelligence, ..관련
- 10. AI, ML, NN, ... 관련
- 11. rest
- 12. Excerpt 1 - 통계, 모멘트
- 13. Excerpt 2 - 확률분포
- 14. 인용
- 15. Cmts
4. 물성전자 ¶
결정질 crystalline
격자 lattice
격자점 lattice point
단위격자, 단위셀 unit lattice, unit cell
격자에너지,lattice_energy
결정 구조 crystal structure
basis(motif)
단결정 single crystal
다결정 polycrystal
결정입계 grain
격자 lattice
격자점 lattice point
단위격자, 단위셀 unit lattice, unit cell
격자에너지,lattice_energy
결정 구조 crystal structure
basis(motif)
단결정 single crystal
다결정 polycrystal
결정입계 grain
// from KU이철진 강의자료
{
{
고체
반도체 구분 기준: 전기전도도 및 에너지밴드갭(energy band gap)
금속 metal conductor
반금속 반도체 semiconductor
절연체 insulator
전기전도도(σ) 변화반금속 반도체 semiconductor
절연체 insulator
반도체 구분 기준: 전기전도도 및 에너지밴드갭(energy band gap)
도핑(doping): Si에 소량의 불순물을 집어넣어 전기전도도를 변화시키면 다양한 특성을 가짐
반도체 재료
원소 반도체: 한 종류의 원자들로 구성 (Q: 4족 only?)
원소 반도체: 한 종류의 원자들로 구성 (Q: 4족 only?)
Si, Ge
화합물 반도체: 두 종류 이상의 원자들의 화합물로 구성 (4-4족, 3-5족, 2-6족)2원소 화합물: SiGe, SiC, GaN, GaAs, GaP, InP, ZnS, ZnO, CdS, MoS₂, MoSe₂, MoTe₂, WS₂, WSe₂, …
3원소 화합물: InGaN, InGaP, InZnO, AlGaAs, GaAsP, HgCdTe, ...
4원소 화합물: InGaZnO, InGaNP, InGaAsP, InGaAlP, ...
수백가지 물질3원소 화합물: InGaN, InGaP, InZnO, AlGaAs, GaAsP, HgCdTe, ...
4원소 화합물: InGaZnO, InGaNP, InGaAsP, InGaAlP, ...
결정격자 crystal lattices
}
| 결정질, 결정성 고체 | crystalline | 구성 입자의 배열이 규칙적 | 입자 사이의 인력이 균일 | 녹는점이 일정함 |
| 비결정질, 비결정성, 비정질 고체 | amorphous, noncrystalline | 구성 입자의 배열이 불규칙적 | 입자 사이의 인력이 일정하지 않음 | 녹는점이 일정하지 않음 |
4결정계 : 입방체(cubic)에서 격자점 위치에 따른 구분
7결정계 : 단위격자 기하적 형태에 따른 구분
Bravais 격자 (14개)
브라베 격자(Bravais lattice)란 주기성과 규칙성과 반복성을 가진 격자
2차원 브라베 격자는 모두 5가지. 3차원 브라베 격자는 모두 14가지
 브라베_격자
브라베_격자
 Bravais_lattice
Bravais_lattice
https://everything2.com/title/Bravais lattice
= 4결정계 dddddddddd2차원 브라베 격자는 모두 5가지. 3차원 브라베 격자는 모두 14가지
https://everything2.com/title/Bravais lattice
단순 입방 simple cubic sc (primitive cubic pc)
면심 입방 face centered cubic fcc
체심 입방 body centered cubic bcc
저심 입방 base centered cubic
육방밀집구조(hexagonal cubic ; hc)?
= 7결정계 ddddddddddd입방정계 cubic or isometric AKA 등축정계 : sc, bcc, fcc
정방정계 tetragonal
사방정계 orthorhombic
삼방정계 trigonal, rhombohedral
단사정계 monoclinic
육방정계 hexagonal
삼사정계 triclinic
{
점군의 표기법:
쇤플리스 표기법(Schoenflies notation)
헤르만-모갱 표기법(Hermann–Mauguin notation)
콕세터 표기법(Coxeter notation)
오비폴드 표기법(orbifold notation)
3차원에서는 총 32개의 결정학적 점군이 존재헤르만-모갱 표기법(Hermann–Mauguin notation)
콕세터 표기법(Coxeter notation)
오비폴드 표기법(orbifold notation)
}
= 고딩 ddddddddd
결정성 고체의 종류
결정성 고체의 종류
이온 결정 (ex. NaCl, CsCl)
층밀림으로 부스러지는 성질
원자 결정 ex. 다이아몬드C, 흑연C, 석영SiO2
강한 공유 결합을 하고 있어 mp, bp가 높음
대체로 전기 전도성이 없음 (예외: 흑연)
분자 결정강한 공유 결합을 하고 있어 mp, bp가 높음
대체로 전기 전도성이 없음 (예외: 흑연)
ex. 드라이아이스CO2, 아이오딘I2, 얼음H2O
금속 결정5. 전자기학 세종대 서용호 ¶
1강 10:54
여러 장,field quantities 사이의 관계 중 일부의 목록
a partial list of relationships between various field quantities
12:48 Differential and integral formulations
* Differential formula
* Integral formula
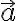 는 unit vector 인듯
는 unit vector 인듯
여러 장,field quantities 사이의 관계 중 일부의 목록
a partial list of relationships between various field quantities
| permittivity (ε) 유전율,permittivity | |
| permeability (μ) 투자율,permeability | |
| conductivity (σ), Ohm's law 컨덕티버티,conductivity 옴_법칙,Ohm_law | |
| Lorentz force equation 로런츠_힘,Lorentz_force | |
| Gauss's law (Maxwell's equation) 가우스_법칙,Gauss_s_law | |
| ditto | |
| continuity equation 연속방정식,continuity_equation | |
| Faraday's law (Maxwell's equation) | |
| Ampere's law (Maxwell's equation) |
12:48 Differential and integral formulations
* Differential formula
* Integral formula
be convenient for performing mathematical operation
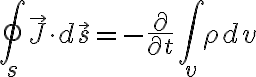
15:49 electrostatic field equations| Coulomb's law: | 쿨롱_법칙,Coulomb_s_law | |
| Electric field: | 전기장,electric_field | |
| Gauss's law: | 가우스_법칙,Gauss_s_law | |
| Convservative | 보존장,conservative_field | |
| Potential function: | 퍼텐셜함수,potential_function | |
| Poisson's equation: | ||
| Laplace's equation: | ||
| Energy density: | 전기에너지밀도,electric_energy_density | |
| Constitutive relationship: | ||
| Ohm's law: | 옴_법칙,Ohm_law |
Time-varying fields
- Maxwell eq.
- Lorentz force eq.
이하 원통좌표계로...............
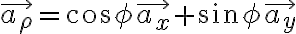
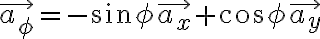
화질 때문에 100% 확신 못함 RE CHK
이하 구면좌표계로......................
differential elements of length, surface, and volume
rectangular coordinate system

rectangular coordinate system

differential volume:
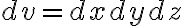
cylindrical coordinate system


differential volume:
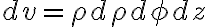
spherical coordinate system


Properties of the gradient of a scalar function
scalar function  에서
에서
The directional derivative of a function at a point in any direction is equal to the dot product of the gradient of the function and the unit vector in that direction.
대충 gradient는 (등고선/equipotential/등고면/등전위선)에 (수직/normal)인 ... 가장 급격하게 변하는....그런 line
cyl. coord:
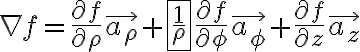
sph. coord:
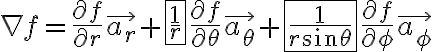
Rect.
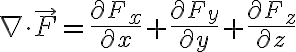
Cyl.
![$\nabla\cdot\vec{F}=\frac1{\rho}\frac{\partial}{\partial \rho}[\rho F_{\rho}]+\frac{1}{\rho}\frac{\partial}{\partial \phi}[F_{\phi}]+\frac{\partial}{\partial z}[F_z]$ $\nabla\cdot\vec{F}=\frac1{\rho}\frac{\partial}{\partial \rho}[\rho F_{\rho}]+\frac{1}{\rho}\frac{\partial}{\partial \phi}[F_{\phi}]+\frac{\partial}{\partial z}[F_z]$](/123/cgi-bin/mimetex.cgi?\Large \nabla\cdot\vec{F}=\frac1{\rho}\frac{\partial}{\partial \rho}[\rho F_{\rho}]+\frac{1}{\rho}\frac{\partial}{\partial \phi}[F_{\phi}]+\frac{\partial}{\partial z}[F_z])
Sph.
![$\nabla\cdot\vec{F}=\frac1{r^2}\frac{\partial}{\partial r}[r^2F_r]+\frac{1}{r\sin\theta}\frac{\partial}{\partial \theta}[\sin\theta F_{\theta}]+\frac{1}{r\sin\theta}\frac{\partial}{\partial \phi}[F_{\phi}]$ $\nabla\cdot\vec{F}=\frac1{r^2}\frac{\partial}{\partial r}[r^2F_r]+\frac{1}{r\sin\theta}\frac{\partial}{\partial \theta}[\sin\theta F_{\theta}]+\frac{1}{r\sin\theta}\frac{\partial}{\partial \phi}[F_{\phi}]$](/123/cgi-bin/mimetex.cgi?\Large \nabla\cdot\vec{F}=\frac1{r^2}\frac{\partial}{\partial r}[r^2F_r]+\frac{1}{r\sin\theta}\frac{\partial}{\partial \theta}[\sin\theta F_{\theta}]+\frac{1}{r\sin\theta}\frac{\partial}{\partial \phi}[F_{\phi}])
Q: 근데 왜 약분을 안하고 이렇게 적었지?
For a continuously differentiable vector field, the net outward flux from a closed surface equals the volume_integral of the divergence throughout the region bounded by that surface.
cell로 나누었음.
안쪽의 겹치는 면은 서로 상쇄되고, 맨 바깥쪽 면만 적분하면 됨.
안쪽의 겹치는 면은 서로 상쇄되고, 맨 바깥쪽 면만 적분하면 됨.
스토크스_정리,Stokes_theorem (curl theorem)
The integral of the normal component of the curl of a vector field over an area is equal to the line integral of the vector field along the curve bounding the area.
ci는 면적 si 주변을 회전하는 그런...?
선이 겹치는 부분은 상쇄되고, 맨 바깥쪽 선만 남는다.
// 정전기1 전하
The Laplacian is a divergence of gradient of a scalar field.
Def.
)
Rect. coord.
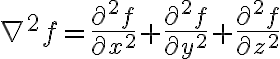
Cyl. coord.
+\frac{1}{\rho^2}\frac{\partial^2 f}{\partial\phi^2}+\frac{\partial^2 f}{\partial z^2})
Sph. coord.
+\frac{1}{r^2\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial f}{\partial\theta}\right)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2 f}{\partial\phi^2})
// 이게 외울 이유는 없을텐데, 어떻게 유도?
아님 다음이 Laplace equation이면 f가 조화함수?
Ex. Prob.
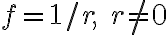 이 Laplace equation의 해임을 보여라
이 Laplace equation의 해임을 보여라
Sol.
스칼라 함수 가 Laplace's equation의 해(solution)가 되려면, ∇²f=0이어야 한다. 구좌표계에서
가 Laplace's equation의 해(solution)가 되려면, ∇²f=0이어야 한다. 구좌표계에서
![$\nabla^2 f=\nabla^2\left[\frac1r\right]$ $\nabla^2 f=\nabla^2\left[\frac1r\right]$](/123/cgi-bin/mimetex.cgi?\Large \nabla^2 f=\nabla^2\left[\frac1r\right])
![$=\frac1{r^2}\frac{\partial}{\partial r}\left[r^2\frac{\partial}{\partial r}\left(\frac1r\right)\right]$ $=\frac1{r^2}\frac{\partial}{\partial r}\left[r^2\frac{\partial}{\partial r}\left(\frac1r\right)\right]$](/123/cgi-bin/mimetex.cgi?\Large =\frac1{r^2}\frac{\partial}{\partial r}\left[r^2\frac{\partial}{\partial r}\left(\frac1r\right)\right])
![$=\frac1{r^2}\frac{\partial}{\partial r}\left[r^2\left(-\frac1{r^2}\right)\right]$ $=\frac1{r^2}\frac{\partial}{\partial r}\left[r^2\left(-\frac1{r^2}\right)\right]$](/123/cgi-bin/mimetex.cgi?\Large =\frac1{r^2}\frac{\partial}{\partial r}\left[r^2\left(-\frac1{r^2}\right)\right])
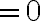
중간에 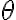 는 상수이므로 없어짐(vanished)
는 상수이므로 없어짐(vanished)
스칼라 함수
Rect. coord.
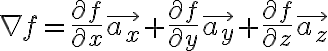
Cyl. coord.
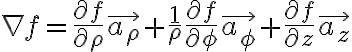
Sph. coord.
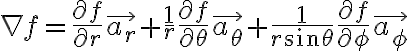
Rect.
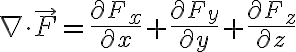
Cyli.
![$\nabla\cdot\vec{F}=\frac1{\rho}\frac{\partial}{\partial\rho}[\rho F_{\rho}]+\frac1{\rho}\frac{\partial}{\partial\phi}[F_{\phi}]+\frac{\partial}{\partial z}[F_z]$ $\nabla\cdot\vec{F}=\frac1{\rho}\frac{\partial}{\partial\rho}[\rho F_{\rho}]+\frac1{\rho}\frac{\partial}{\partial\phi}[F_{\phi}]+\frac{\partial}{\partial z}[F_z]$](/123/cgi-bin/mimetex.cgi?\Large \nabla\cdot\vec{F}=\frac1{\rho}\frac{\partial}{\partial\rho}[\rho F_{\rho}]+\frac1{\rho}\frac{\partial}{\partial\phi}[F_{\phi}]+\frac{\partial}{\partial z}[F_z])
Sph.
![$\nabla\cdot\vec{F}=\frac1{r^2}\frac{\partial}{\partial r}[r^2 F_r]+\frac1{r\sin\theta}\frac{\partial}{\partial\theta}[\sin\theta F_{\theta}]+\frac1{r\sin\theta}\frac{\partial}{\partial\phi}[F_{\phi}]$ $\nabla\cdot\vec{F}=\frac1{r^2}\frac{\partial}{\partial r}[r^2 F_r]+\frac1{r\sin\theta}\frac{\partial}{\partial\theta}[\sin\theta F_{\theta}]+\frac1{r\sin\theta}\frac{\partial}{\partial\phi}[F_{\phi}]$](/123/cgi-bin/mimetex.cgi?\Large \nabla\cdot\vec{F}=\frac1{r^2}\frac{\partial}{\partial r}[r^2 F_r]+\frac1{r\sin\theta}\frac{\partial}{\partial\theta}[\sin\theta F_{\theta}]+\frac1{r\sin\theta}\frac{\partial}{\partial\phi}[F_{\phi}])
// 이거 위에도 있는데 또 적었네........ dupe.
Rect.
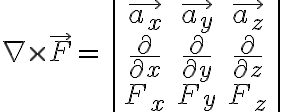
Cyli.
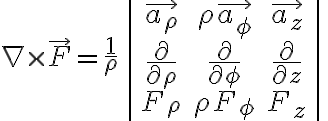
Sphe.
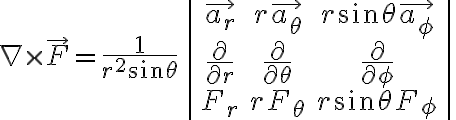
The divergence thm 발산정리,divergence_theorem
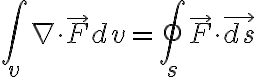
Stokes' thm 스토크스_정리,Stokes_theorem
\cdot\vec{ds}=\oint_c\vec{F}\cdot\vec{d\ell})
Green's first identity
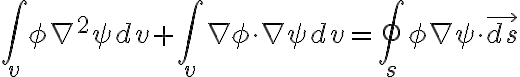
Green's second identity (Green's thm) 그린_정리,Green_theorem
![$\int_v[\phi\nabla^2\psi-\psi\nabla^2\phi]dv=\oint_s[\phi\nabla\psi-\psi\nabla\phi]\cdot\vec{ds}$ $\int_v[\phi\nabla^2\psi-\psi\nabla^2\phi]dv=\oint_s[\phi\nabla\psi-\psi\nabla\phi]\cdot\vec{ds}$](/123/cgi-bin/mimetex.cgi?\Large \int_v[\phi\nabla^2\psi-\psi\nabla^2\phi]dv=\oint_s[\phi\nabla\psi-\psi\nabla\phi]\cdot\vec{ds})
Chapter III Electrostatics
1 Intro
2 쿨롱법칙 쿨롱_법칙,Coulomb_s_law
3 전기장세기,electric_field_intensity
4 전속,electric_flux and 전속밀도,electric_flux_density
5 전위,electric_potential
6 전기쌍극자,electric_dipole
7 Materials in an 전기장,electric_field
1 Intro
2 쿨롱법칙 쿨롱_법칙,Coulomb_s_law
3 전기장세기,electric_field_intensity
4 전속,electric_flux and 전속밀도,electric_flux_density
5 전위,electric_potential
6 전기쌍극자,electric_dipole
7 Materials in an 전기장,electric_field
전기장세기,electric_field_intensity는
- conservative (보존적인 계)
- irrotational (비회전계)
쿨롱 법칙 설명 중 뉴턴 2법칙과 중첩원리,superposition_principle 등 언급.
여러 전하(system of n point charges)가 점전하 q에 미치는 힘의 총합은 각 힘의 합이니까 당연히
}{4\pi\epsilon_0|\vec{r}-\vec{r_i}|^3})
전기장 세기는 단위전하당 힘이므로 N/C
선전하밀도 line charge density
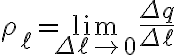
표면전하밀도 surface charge density
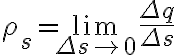
체적전하밀도 volume charge density
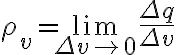
전속,electric_flux의 정의
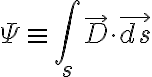
가우스_법칙,Gauss_s_law
폐곡면을 통해 밖으로 나가는 알짜유출선속은, 그 폐곡면 내부 알짜 전하와 같다
The net outward flux passing through a closed surface is equial to the total charge enclosed by that surface
Proof:
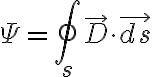
여기서 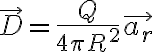 이므로
이므로

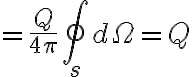
(Ω : solid_angle)
V/m도 같음
전하밀도,charge_density선전하밀도 line charge density
폐곡면을 통해 밖으로 나가는 알짜유출선속은, 그 폐곡면 내부 알짜 전하와 같다
The net outward flux passing through a closed surface is equial to the total charge enclosed by that surface
Proof:
전기장 안에서 전하가 움직이면, 전기장이 전하에 한 일
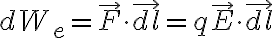
반면, 외력(external force)이 전하를 움직였다면, 외력이 한 일은
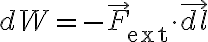
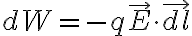
외력이 전하를 b에서 a까지 움직이면서 한 일
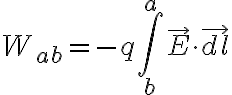
(그림에선 a와 b를 잇는 연결선이 있고 그 위 한 점에 q가 있으며, q에서 연결선 접선 방향으로의 미소길이가 dl. E의 방향은 물론 그 연결선과 무관하며, lines of force 방향임. Fext와 qE의 방향은 정반대.)
eeeeeeeeeeeeee
Classification of fields
Class I fields
Class I fields
Class II fields
Class III fields
7. 허블 법칙 ¶
외부 은하의 적색편이,redshift(도플러_효과,Doppler_effect)를 관찰한 결과, 멀리 있는 은하일수록 더 빨리 멀어짐.
외부 은하가 멀어지는 속도 (후퇴 속도)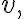 은하까지의 거리
은하까지의 거리  이면
이면
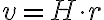
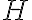 는 허블 상수 (73 km/s/Mpc)
는 허블 상수 (73 km/s/Mpc)
외부 은하가 멀어지는 속도 (후퇴 속도)
8. 우주의 나이 구하기 ¶
우주가 지금과 같은 속도로 팽창해 왔다고 가정.
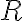 만큼 떨어진 외부 은하가
만큼 떨어진 외부 은하가 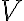 의 속도로 멀어지고 있으면 허블 법칙에 따라
의 속도로 멀어지고 있으면 허블 법칙에 따라
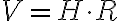
거리를 후퇴 속도로 나누면 우주의 나이 (허블 시간) 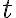 를 구할 수 있으며, 허블 상수의 역수와 같음
를 구할 수 있으며, 허블 상수의 역수와 같음
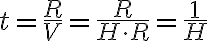
}
9.1. 키워드.. ¶
1. 하루에 7시간 30분 이상 공부하지 말 것. 그 이상은 당신을 지치게 할 것이다.
2. 일주일에 하루를 쉬고 그 하루는 당신이 좋아하는 것을 하라. 당신은 배움을 하는 것이지 일찍 죽으려는 것이 아니다.
3. 각 과목에서 가장 중요한 지식에 집중을 해라. 그 지식의 50%를 먼저 이해하기 위해 계획을 세워라.
4. 낮은 난이도에서 높은 난이도로 공부해라. 큰 틀을 공부하고 디테일을 채우자. 공부한 부분을 요약하는 것이 중요하다.
5. 낮잠을 자라. 그 것은 기분을 새롭게 하고 공부한 것을 기억할 확률을 높여준다. (기상 7~8시간 이후, 30분을 넘기지 말 것.)
6. 2시간 30분 정도 한 주제를 공부하라. 그런 다음 다른 것으로 전환하라.
7. 공부한 것을 내려 놓고 요약해보라. 요약할 때는 읽은 내용을 보지 않고 하는 것이 좋다. 기억하는 연습을 해야 한다.
10. AI, ML, NN, ... 관련 ¶
AI(인공지능,artificial_intelligence),
ML(기계학습,machine_learning), 머신러닝
NN 신경망,neural_network,
패턴인식,pattern_recognition,
computer_vision,
etc.
ML(기계학습,machine_learning), 머신러닝
NN 신경망,neural_network,
패턴인식,pattern_recognition,
computer_vision,
etc.
기술:
주성분분석,principal_component_analysis,PCA
독립성분분석,independent_component_analysis,ICA
최대가능도추정,maximum_likelihood_estimation,MLE
특이값분해,singular_value_decomposition,SVD
고유값분해,eigendecomposition or 고유분해,eigendecomposition
자연어처리,natural_language_processing,NLP
주성분분석,principal_component_analysis,PCA
독립성분분석,independent_component_analysis,ICA
최대가능도추정,maximum_likelihood_estimation,MLE
특이값분해,singular_value_decomposition,SVD
고유값분해,eigendecomposition or 고유분해,eigendecomposition
자연어처리,natural_language_processing,NLP
교양, 기반지식, 관련분야, 관련 키워드:
철학,philosophy
논리,logic
마인드,mind 마음으로 번역되는 경우가 많음, 정신활동?
뇌,brain
뇌파,brainwave = 뇌전도,electroencephalography,EEG
신경세포 뉴런 neuron 신경단위 - 뉴런,neuron
시냅스 synapse 연접
신경전달물질 neurotransmitter
신경과학 neuroscience
심리학,psychology
정신의학,psychiatry
인지,cognition
인지과학,cognitive_science, cogsci
인지심리학,cognitive_psychology
커넥텀 커넥톰 connectome
네트워크,network 네트웍
기억,memory
생리학,physiology
퍼셉트론,perceptron
지각,perception
학습 배움 learning
역전파,backpropagation
언어학,linguistics
언어,language
추리 reasoning inference deduction // inference의 페이지명은 추론,inference으로 정함.. deduction은 연역,deduction으로 정함..
의식,consciousness
{
http://www.aistudy.co.kr/psychology/consciousness.htm
}
지식,knowledge
{
지식베이스,knowledge_base / 지식기반,knowledge_base ? knowledge_base
knowledge_base
음성인식 speech_recognition speech_recognition
speech_recognition
로봇 robot
로봇공학 robotics
퍼지,fuzzy
멤리스터,memristor
프롤로그,Prolog
리스프,Lisp
철학,philosophy
논리,logic
마인드,mind 마음으로 번역되는 경우가 많음, 정신활동?
뇌,brain
뇌파,brainwave = 뇌전도,electroencephalography,EEG
신경세포 뉴런 neuron 신경단위 - 뉴런,neuron
시냅스 synapse 연접
신경전달물질 neurotransmitter
신경과학 neuroscience
심리학,psychology
정신의학,psychiatry
인지,cognition
인지과학,cognitive_science, cogsci
인지심리학,cognitive_psychology
커넥텀 커넥톰 connectome
네트워크,network 네트웍
기억,memory
생리학,physiology
퍼셉트론,perceptron
지각,perception
학습 배움 learning
강화학습,reinforcement_learning
기계학습,machine_learning
심층학습,deep_learning
지도학습,supervised_learning
자율학습 or 비지도학습,unsupervised_learning
사고 생각 thinking기계학습,machine_learning
심층학습,deep_learning
지도학습,supervised_learning
자율학습 or 비지도학습,unsupervised_learning
역전파,backpropagation
언어학,linguistics
언어,language
추리 reasoning inference deduction // inference의 페이지명은 추론,inference으로 정함.. deduction은 연역,deduction으로 정함..
의식,consciousness
{
http://www.aistudy.co.kr/psychology/consciousness.htm
cmp or sub: 무의식, 비의식, 의식불명, ..., 잠재의식, ...
similar: 자각 (awareness), perception, ...
https://everything2.com/title/Consciousnesssimilar: 자각 (awareness), perception, ...
}
지식,knowledge
{
prior_knowledge =,prior_knowledge . prior_knowledge
}지식베이스,knowledge_base / 지식기반,knowledge_base ?
음성인식 speech_recognition
로봇 robot
로봇공학 robotics
퍼지,fuzzy
퍼지논리,fuzzy_logic
퍼지집합,fuzzy_set
생체모방 biomimetics, biomimicry퍼지집합,fuzzy_set
멤리스터,memristor
프롤로그,Prolog
리스프,Lisp
11. rest ¶
\;의 사용
 - ugly
- ugly
 - better
- better
rfr:
과도에서찾아볼책
{
(인텔 프로세서를 위한) 시스템 프로그래밍 제2판(개정판)
https://library.korea.ac.kr/search/detail/CATTOT000045830059?briefLink=/searchMain/mashupResult?q=인텔 프로세서를 위한#.XI-pNbhS-Uk
{
(인텔 프로세서를 위한) 시스템 프로그래밍 제2판(개정판)
https://library.korea.ac.kr/search/detail/CATTOT000045830059?briefLink=/searchMain/mashupResult?q=인텔 프로세서를 위한#.XI-pNbhS-Uk
IBM PC 매크로 어셈블리 프로그래밍
YTHA YU. CHARLES MARUT 저 / 이재광 역
Assembly language programming and organization of the IBM PC
소장처 과학도서관/단행본실(2층)/
청구기호 005.265 Y94a
등록번호 421116962
YTHA YU. CHARLES MARUT 저 / 이재광 역
Assembly language programming and organization of the IBM PC
소장처 과학도서관/단행본실(2층)/
청구기호 005.265 Y94a
등록번호 421116962
(매크로 어셈블리)윈도우즈프로그래밍
소장처 과학도서관/보존서고5(동양서)/
청구기호 005.265 2000f
소장처 과학도서관/보존서고5(동양서)/
청구기호 005.265 2000f
}
apostrophe  vs super-prime
vs super-prime 
str inside backtick: xyz
test 
벡터표현 using 특수문자
2v⃗+w⃗=0⃗
a⃗b⃗c⃗d⃗e⃗f⃗g⃗
A⃗B⃗C⃗D⃗E⃗f⃗G⃗
벡터표현 using mathml
2v⃗+w⃗=0⃗
a⃗b⃗c⃗d⃗e⃗f⃗g⃗
A⃗B⃗C⃗D⃗E⃗f⃗G⃗
벡터표현 using mathml
RSA 암호
특징: 복호화 과정을 비밀에 붙인다면, 암호화 과정은 공개해도 무방하다는 것.
모든 공개키암호화의 특징일듯? CHK
Alice가 Bob에게 비밀 메시지를 보내려 한다고 가정한다. 그러기 전에 둘은 큰 (적어도 수백 자릿수의) 소수 p와 q를 정한 다음, 둘을 곱하여 M=pq를 얻는다. 원한다면 이 수는 공개할 수도 있다. 둘은 또한 K=(p-1)(q-1)을 계산한 다음 이것은 비밀로 간직한다.이제 Alice는 메시지를 0에서 M까지의 한 수로 표현한다 (아주 긴 메시지라면 그런 수들의 조합으로 표현한다). 메시지를 암호화하기 위해 Alice는 K와 공약수가 없는 어떤 수 a를 선택하고, y=-xa(mod M)을 계산한다. 수 a는 Bob에게는 반드시 알려주어야 하며, 또 원한다면 공개할 수도 있다.
메시지를 복호화하려면 Bob은 다음 조건을 만족하는 수 b를 알아야만 한다. ab≡1(mod K). (유일한 값으로 존재하는) 이 수는 둘만 아는 비밀로 한다. y를 풀기 위해, Bob은 다음을 계산한다.
yb(mod M)
왜 이렇게 하는 것일까?yb≡(xa)b≡xab≡x1≡x(mod M)
이는 오일러가 일반화시킨 페르마의 소정리를 이용한 결과다.이 방법이 실용적인 까닭은 큰 소수를 찾는 효과적인 방법은 있는 반면에 큰 소수의 소인수를 찾는 효과적인 방법은 없기 때문이다. 따라서 곱 pq를 알려준다고 해서 사람들이 p와 q를 찾기는 무척 어렵기에, 이 두 수를 모르는 한 값 b를 알아낼 수 없고, 결국 메시지를 풀 수 없다.
(교양인을 위한 수학사 강의) -- user4 2019-09-30 23:35:41
IMRaD/IMRAD model/structure/format
IMRAD(임래드)는 과학 논문의 일반적 형태로서, 4~5개의 주 부분(섹션, section)으로 구성된다.
과학에서 학문적 목적으로 쓰여진 글은 보통 IMRaD 모델을 따른다. 그 뜻은,
- Introduction 소개
- Method (연구)방법
- Results 결과
- and 그리고
- Discussion 토의
맨 처음 부분인 abstract(개요, 초록)은,
내용에선
비유적이고 감정적인(figurative and emotional) 언어를 삼간다.
- 본문의 요약(summary)역할을 한다.
- 전체 글을 읽을지 독자에게 정보를 주는 역할을 한다.
- 보통 250단어보다 짧다.
내용에선
비유적이고 감정적인(figurative and emotional) 언어를 삼간다.
소개 부분에서는 논문의 모티브(motivation), 목적, 문제, 시험된 가설, 새로운 기여, 배경 등을 설명한다.
...
Keywords: 학문적 글쓰기(academic writing), 과학 논문(scientific paper),
Sites
How to Organize a Paper: The IMRaD Format
https://thevisualcommunicationguy.com/writing/how-to-organize-a-paper/how-to-organize-a-paper-the-imrad-format/ -- user4 2019-10-22 05:16:26
How to Organize a Paper: The IMRaD Format
https://thevisualcommunicationguy.com/writing/how-to-organize-a-paper/how-to-organize-a-paper-the-imrad-format/ -- user4 2019-10-22 05:16:26
12. Excerpt 1 - 통계, 모멘트 ¶
// tmp excerpts; 통계학 기초; KU유철상 자재이 p152-159
통계학이란?
통계학은 굉장히 다양한 분야를 포괄하고 있지만 크게 보면 통계학statistics, 확률론probability 그리고 확률과정론stochastic process등으로 나눌 수 있다. 통계학은 주로 관측자료를 다룬다는 측면에서 과거에 초점을 맞추는 경향이 있다. 이와 반대로 확률론은 아직 발생하지 않은 미래를 예측(예측,prediction) 하는 일이다. 마지막으로 확률과정론에서는 현재에서 미래로 어떻게 변해가는지에 관심이 있다. 이런 이유로 확률과정론을 통계학의 동역학이라고 부르기도 한다. 이들 중 여기서 살펴보는 내용은 주로 통계학이다. 즉, 주로 관측자료를 정리할 때 사용하는 내용들이다.
통계학에서 다루는 내용은 너무 다양하다. 회귀분석,regression_analysis이라는 주제는 매우 보편적이다. 이와 관련한 너무나 다양한 종류의 통계분석이 있다. 요인분석factor_analysis, 군집분석cluster_analysis, 주성분분석principal component analysis(주성분분석,principal_component_analysis,PCA) 등등. 분산분석analysis of variance(ANOVA)은 회귀분석에 가까운 분석이다. 가설검정,hypothesis_test도 중요한 주제이고, 빈도해석,frequency_analysis 은 특히 공학에서 중요하다. 그러나 저자는 이런 주제들을 공부할 때 가장 중요한 것이 모멘트,moment의 개념과 확률분포,probability_distribution에 대한 이해라고 생각한다. 단순선형회귀분석 simple_linear_regression_analysis 에 대한 심도 있는 이해는 매우 다양하고 복잡한 형태의 회귀분석을 습득하는데 필요한 기초를 제공해 준다 (그러나 이 내용은 다루지 않았다).
/*
요인분석,factor_analysis
군집분석,cluster_analysis ........ 군집,cluster
주성분분석,principal_component_analysis,PCA
//분산분석,analysis_of_variance
분산분석,variance_analysis
*/
요인분석,factor_analysis
군집분석,cluster_analysis ........ 군집,cluster
주성분분석,principal_component_analysis,PCA
//분산분석,analysis_of_variance
분산분석,variance_analysis
analysis of variance
이건 회귀분석에 가까운 분석.
QQQ 그럼 회귀분석 - 분산분석 차이?
빈도분석,frequency_analysis or 빈도해석 .... 빈도,frequency 분석,analysis이건 회귀분석에 가까운 분석.
QQQ 그럼 회귀분석 - 분산분석 차이?
*/
모멘트는 중고등학교 시절 물리학 시간에 많이 사용하였다. 당시 모멘트는 힘,force과 작용점까지의 거리,distance의 곱으로 정의했었다. 그러나 정확히 살펴보면 이건 1차 모멘트의 개념이다. 모멘트는 1차부터 n차까지 다양하게 정의 가능하다.
사실 모멘트 개념은 이미 초등학교부터 심도있게 사용되었다. 예를 들어, 관찰한 자료를 정리한 것이 도수분포표 frequency distribution table 이고, { 그러고보니 도수=frequency 분포=distribution 표=table ... see frequency_table . 그리고 distribution 빼도 의미 같은지 chk }
이 표가 주어지면 여러분들은 주어진 자료의 평균,mean,average과 분산,variance을 계산하는 방법을 배웠다.
평균을 계산할 땐 1차모멘트 개념을 이용했고,
분산을 계산할 땐 2차모멘트 개념을 이용했다.
이 표가 주어지면 여러분들은 주어진 자료의 평균,mean,average과 분산,variance을 계산하는 방법을 배웠다.
평균을 계산할 땐 1차모멘트 개념을 이용했고,
분산을 계산할 땐 2차모멘트 개념을 이용했다.
평균 계산 방법을 식으로 나타내면:
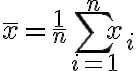
위 식에서
 는 각 자료를,
는 각 자료를,
 은 자료의 개수를,
은 자료의 개수를,
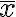 는 평균을 의미한다.
는 평균을 의미한다.
같은 자료가 여러 개 존재하거나 또는 유사한 그룹으로 자료를 구분할 수 있다면 위 식은 다음과 같이 바꿔 표현할 수 있다.
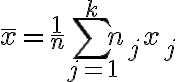
위 식에서
당연히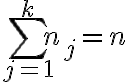 이다.
이다.
당연히
마지막으로, 어떤 특정 자료가 모집단family(sic. chk)에서 어떤 확률로 존재하는지가 정해져 있다면 위 식은 다음과 같이 변경될 수 있다.
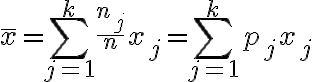
위 식에서 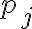 는
는 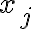 를 대표하는 확률로 정의된다.
를 대표하는 확률로 정의된다.
만일 이산형태의 자료가 아니고 연속형태의 자료라면 합의 기호 ) 가 들어간 위 식은 적분기호
가 들어간 위 식은 적분기호 ) 가 들어간 식으로 바꿀 수 있다. 이 때 추가로 연속된 자료가 어떻게 분포되어 있는지가 정해져야 하는데 이를 확률밀도함수,probability_density_function,PDF라고 한다. 확률밀도함수는 이산확률
가 들어간 식으로 바꿀 수 있다. 이 때 추가로 연속된 자료가 어떻게 분포되어 있는지가 정해져야 하는데 이를 확률밀도함수,probability_density_function,PDF라고 한다. 확률밀도함수는 이산확률 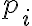 를 연속된 공간으로 확장한 것과 같다. 즉 위 식을 적분기호가 들어간 식으로 바꾸어 보면
를 연속된 공간으로 확장한 것과 같다. 즉 위 식을 적분기호가 들어간 식으로 바꾸어 보면
 x dx=\int_{-\infty}^{\infty} x f(x) dx)
위 식에서 두 번째 등호 이후의 식은 단순히  를
를 ) 앞으로 보낸 형태를 표시한 것이다. 위 식에서
앞으로 보낸 형태를 표시한 것이다. 위 식에서  는 임의의 값이며 확률변수,random_variable라고 부른다.
는 임의의 값이며 확률변수,random_variable라고 부른다. ) 는
는  의 확률밀도함수이다. 만일
의 확률밀도함수이다. 만일  가 특정 범위에서만 정의된다면 위 적분은 그 범위로 한정하여 표현할 수 있다. 바로 이 식이 주어진 pdf에 대한 평균을 계산하는 식이다.
가 특정 범위에서만 정의된다면 위 적분은 그 범위로 한정하여 표현할 수 있다. 바로 이 식이 주어진 pdf에 대한 평균을 계산하는 식이다.
또는 주어진 pdf의 원점에 대한 1차 모멘트(first-order moment of the given probability function about the orgin) 라고 부른다.
또는 주어진 pdf의 원점에 대한 1차 모멘트(first-order moment of the given probability function about the orgin) 라고 부른다.
위 식을 1차 모멘트라고 부르는 이유는 다음 식과 같다.
 dx = \int_{-\infty}^{\infty} x^1 f(x) dx)
즉 위 식의 가장 오른쪽 표현처럼 '1' 이라는 숫자가  의 지수로 붙어 있기 때문이다. 이 지수가 2이면 2차 모멘트이고, n이면 n-차 모멘트라고 부른다. 즉, 주어진 pdf의 원점에 대한 n-차 모멘트는 다음과 같이 정의된다.
의 지수로 붙어 있기 때문이다. 이 지수가 2이면 2차 모멘트이고, n이면 n-차 모멘트라고 부른다. 즉, 주어진 pdf의 원점에 대한 n-차 모멘트는 다음과 같이 정의된다.
 dx)
참고로, 우리가 잘 아는 분산,variance은 평균에 대한 2차 모멘트로 정의된다. 즉
^2 f(x) dx)
위 식을 곰곰이 살펴보면, 분산은 각 자료에서 평균을 뺀 후 제곱해서 더한 후 자료의 개수로 나누어 계산하면 된다는 것을 뜻한다. 위 식을 여러분이 알고 있는 형태로 다시 쓰면,
^2)
3차 모멘트는 왜곡도skewness(왜도,skewness), 즉 확률밀도함수가 한쪽으로 치우친 정도를 판단하는 데 사용한다. 좌우 대칭인 정규분포는 왜곡도가 0이다. 대수정규분포log-normal distribution 는 보통 오른쪽으로 긴 꼬리를 갖는 형태인데, 이런 형태일 경우 양의 왜곡도를 갖는다.
4차 모멘트는 첨도peakedness(첨도,kurtosis? chk)를 측정하는 데 사용된다. 첨도는 정규분포를 기준으로 얼마나 뾰족한지를 측정하는 척도로 pdf의 꼬리가 얼마나 두꺼운지를 판단할 때도 쓰인다.
이제 정규분포normal distribution(정규분포,normal_distribution)의 예를 들어보자. 정규분포는 평균과 표준편차를 모수로 갖는다. 통상 ) 으로 표현하는데, 여기서 μ와 σ가 모수가 된다. 모수,parameter는 모집단,population의 특성을 대표하는 값으로 참값에 해당한다. 표본sample(표본,sample)을 가지고 추정한 값은 추정치estimate(추정값,estimate)라고 부른다. 따라서 모수추정parameter estimation은 주어진 표본을 가지고 모집단의 특성을 추정하는 과정이다. 기본적으로 표본을 가지고 추정한 다양한 모멘트는 모집단의 모멘트와 같다는 가정이 전제된다.
으로 표현하는데, 여기서 μ와 σ가 모수가 된다. 모수,parameter는 모집단,population의 특성을 대표하는 값으로 참값에 해당한다. 표본sample(표본,sample)을 가지고 추정한 값은 추정치estimate(추정값,estimate)라고 부른다. 따라서 모수추정parameter estimation은 주어진 표본을 가지고 모집단의 특성을 추정하는 과정이다. 기본적으로 표본을 가지고 추정한 다양한 모멘트는 모집단의 모멘트와 같다는 가정이 전제된다.
먼저 주어진 정규분포함수에 대해 1차 모멘트를 구하면 평균 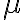 가 유도된다.
가 유도된다.
또한 평균에 대한 2차 모멘트를 구하면 분산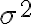 가 유도된다.
가 유도된다.
이 값에 제곱근을 취한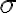 가 표준편차이다. 이 값들은 모두 이론적으로 유도되는 값이며 모집단의 특성이다.
가 표준편차이다. 이 값들은 모두 이론적으로 유도되는 값이며 모집단의 특성이다.
이제 주어진 표본에 대해 우리가 알고 있는 공식을 이용하여 평균과 표준편차를 계산할 수 있다. 이를 각각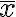 와
와 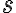 라고 하자. 모수와 다른 기호를 사용한 이유는 표본을 이용하여 구했다는 것을 나타내기 위해서이다. 따라서 이를 표본평균, 표본표준편차 라고 부르기도 한다.
라고 하자. 모수와 다른 기호를 사용한 이유는 표본을 이용하여 구했다는 것을 나타내기 위해서이다. 따라서 이를 표본평균, 표본표준편차 라고 부르기도 한다.
// 표본평균,sample_mean 표본표준편차,sample_standard_deviation
또한 평균에 대한 2차 모멘트를 구하면 분산
이 값에 제곱근을 취한
이제 주어진 표본에 대해 우리가 알고 있는 공식을 이용하여 평균과 표준편차를 계산할 수 있다. 이를 각각
// 표본평균,sample_mean 표본표준편차,sample_standard_deviation
결과적으로 모멘트의 개념을 이용한 모수추정은 이론적인 확률밀도함수의 모멘트와 표본을 가지고 구한 모멘트를 같다고 가정하는 과정이다. 즉,
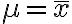
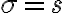
만일 평균이나 표준편차가 모수들의 결합으로 나타난다면(정규분포의 경우는 그렇지 않지만), 주어진 연립방정식을 풀어 모수를 결정하게 된다. 모수가 2개인 경우에는 평균, 분산을 이용하고, 모수가 3개인 경우에는 일반적으로 평균, 분산, 왜곡도가 이용된다.
마지막으로, 연습 삼아 다음과 같은 균등분포(고른분포,uniform_distribution)의 평균과 분산을 구해보기로 하자. 균등분포는 균일분포 또는 일양분포라고 부르기도 한다. 그러나 이렇게 가장 단순하게 생긴 pdf인 균등분포는 실제는 매우 중요하다. Fortran의 난수발생기random number generator ran 은 가장 간단한 균등분포, 즉 하한계가 0이고 상한계가 1인 ) 의 난수를 발생시켜 준다. 다른 경우나 다른 확률밀도함수를 따르는 경우는 모두 이 난수를 이용하여 만들어 주어야 한다. 예를 들어 정규분포를 따르는 난수도 균등분포를 따르는 난수를 적절히 조합해서 다시 만든다. 이를 위해서는 소위 알고리듬,algorithm이 먼저 만들어져야 하고, 다음으로 이를 프로그램화해야 한다. 좋은 알고리듬을 만들기 위해서는 많은 수학적 지식이 필요하다.
의 난수를 발생시켜 준다. 다른 경우나 다른 확률밀도함수를 따르는 경우는 모두 이 난수를 이용하여 만들어 주어야 한다. 예를 들어 정규분포를 따르는 난수도 균등분포를 따르는 난수를 적절히 조합해서 다시 만든다. 이를 위해서는 소위 알고리듬,algorithm이 먼저 만들어져야 하고, 다음으로 이를 프로그램화해야 한다. 좋은 알고리듬을 만들기 위해서는 많은 수학적 지식이 필요하다.
하한이 0이고 상한이 1인 균등분포의 pdf는 다음과 같다.
=\begin{cases}1,&0 \le x \le 1\\0,&x<0 \,\textrm{ or }\, x>1\end{cases})
먼저, 평균을 구하면 다음과 같다.
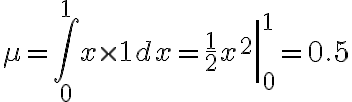
분산도 다음과 같이 쉽게 계산할 수 있다.
^2 \times 1 dx)
 \times 1 dx)
\right|_0^1=\frac1{12})
13. Excerpt 2 - 확률분포 ¶
정규분포,normal_distribution에서 정규normal은 사실 정상이라는 뜻이다. 처음 정규분포가 발표됐을 때 이 분포를 따르지 않는 자료는 모두 잘못된 것이란 믿음이 있었다. 그래서 그런 자료는 모두 비정상abnormal이라 간주되었다. 이는 물론 사실이 아니다. 최근에는 이 정규라는 이름의 문제점을 고려하여 정규분포를 유도한 가우스의 이름을 따 가우스 분포 Gaussian_distribution 라고 부르는 경우가 많다. 그러나 우리는 정규분포라는 이름이 익숙하고, 또 이름에 정상/비정상의 뜻이 있었는지 잘 모르므로 그냥 정규분포라고 부르기로 한다.
정규분포는 그냥 하늘에서 떨어진 것이 아니고 유도된 것이다. 여기서는 확률밀도함수가 어떤 과정을 통해 유도되는지에 대해 살펴보기로 한다. 이 유도과정에서 가장 중요한 개념이 베르누이_시행,Bernoulli_trial이다. 이것의 가장 간단한 예가 동전던지기 coin_toss 이다. ({T, F} 확률이 {0.5, 0.5}, 앞면 또는 뒷면의 발생은 서로 독립independent(독립성,independence) - 서로 영향을 주지 않음) 주사위 두 개 던지기도 경우의 수가 많아져서 그렇지 역시 베르누이시행의 좋은 예.
베르누이 시행을 반복하면 다양한 분포함수,distribution_function가 만들어진다. 동전던지기를 100회 했다고 가정하자. 이 때 앞면이 50번 나올 확률은 쉽게 계산할 수 있다. 물론 앞면이 한 번도 나오지 않는 경우의 확률도 계산할 수 있다. 결과적으로 앞면이 0에서 100번 나오는 경우 모두의 확률을 계산할 수 있다. 그렇다면 이 확률을 앞면의 발생횟수에 대응시켜놓으면 어떤 모양이 될까? 이 분포를 이항분포,binomial_distribution라고 한다. (0.5, 0.5 뿐만 아니라) 임의의 성공확률  실패확률
실패확률 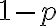 인 경우에도 동일하게 확률분포를 유도할 수 있다. 역시 이항분포라고 부른다.
인 경우에도 동일하게 확률분포를 유도할 수 있다. 역시 이항분포라고 부른다.
성공확률이 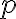 인 시행을 독립적으로 반복하는 베르누이_시행 에서
인 시행을 독립적으로 반복하는 베르누이_시행 에서  번째 성공이 일어날 때까지의 시행횟수의 확률분포를 음이항분포,negative_binomial_distribution라고 한다. 또한, 성공횟수
번째 성공이 일어날 때까지의 시행횟수의 확률분포를 음이항분포,negative_binomial_distribution라고 한다. 또한, 성공횟수 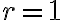 인 음이항분포, 즉 처음 성공할 때까지의 베르누이_시행,Bernoulli_trial 횟수의 분포는 기하분포,geometric_distribution라고 부른다.
인 음이항분포, 즉 처음 성공할 때까지의 베르누이_시행,Bernoulli_trial 횟수의 분포는 기하분포,geometric_distribution라고 부른다.
정규분포는 성공확률 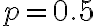 인 이항분포,binomial_distribution에서 시행횟수를 무한히 늘리면 만들어지는 분포이다. Gauss가 처음 유도하였다.
인 이항분포,binomial_distribution에서 시행횟수를 무한히 늘리면 만들어지는 분포이다. Gauss가 처음 유도하였다.
사실 정규분포는 자연현상과는 거리가 있다. 자연현상과 관련된 자료 중 정규분포를 따르는 자료는 거의 없다. 오히려 대수정규분포를 따르는 자료가 많다.
사실 정규분포는 자연현상과는 거리가 있다. 자연현상과 관련된 자료 중 정규분포를 따르는 자료는 거의 없다. 오히려 대수정규분포를 따르는 자료가 많다.
// 페이지이름 결정안됨..... 로그정규분포 , lognormal_distribution , log-normal_distribution , ... curr at 확률분포,probability_distribution Sub 중에 있음 //
대수정규분포log-normal distribution는 정규분포를 따르는 자료에 지수exponential(지수,exponentiation)를 취하면 만들어지는 분포이다. 거꾸로 대수정규분포를 따르는 자료에 대수logarithm(로그,log)를 취하면 정규분포를 따르게 된다. 지수를 취하는 경우 큰 자료는 상상도 할 수 없을 정도로 커지지만 작은 자료는 반대로 엇비슷한 값으로 조정된다.
정규분포 따르는 자료를 곱한 값이나 곱한 값을 더한 경우에는 카이제곱chi-square분포를 따른다. (카이제곱분포,chi-squared_distribution) 카이제곱분포는 두 자료의 차이가 아니라, 차이의 제곱을 가지고 통계적으로 비교하는 경우에 많이 사용되는 분포이다. 이와 유사하지만 분산,variance을 비교하는 경우에는 제곱의 합을 총 돗수로 나누는 형태가 되는데, 이는 F-분포(F분포,F-distribution)를 따르게 된다.
다시 이항분포로 돌아가 보자. 이항분포는 매우 유용한 분포함수인데, 문제는 베르누이 시행의 횟수 n이 증가하는 경우이다. 이 때 확률 계산을 위해서는 팩토리얼factorial을 계산하여야 되는데 이게 문제이다. n이 100보다 크기만 해도 단순하지 않다. 이런 문제를 해결하기 위해 베르누이 분포의 근사분포가 유도되었는데, 이것이 포아송Poisson분포(푸아송_분포,Poisson_distribution)이다. 포아송분포는 이항분포,binomial_distribution와 근본적으로 같다. 그러나 성공확률이 매우 작고 반대로 시행횟수는 매우 큰 경우에 적용되는 분포라고 생각하면 된다. 결과적으로 중요한 차이가 나타나는데 이항분포는 합의 기호가 들어간 이산discrete분포가 되는데 반해, 포아송분포는 연속함수로 되어 있다. 연속함수의 장점은 물론 미분, 적분이 쉬워진다는 점이다.
포아송분포를 이용하면 다양한 확률분포를 유도할 수 있다. 먼저 사건,event의 발생이 포아송분포를 따른다는 전제하에 (첫 번째 사건이 발생할 때까지의 시간,time) 또는 (사건과 사건 사이의 시간 간격 { time_interval ? } )은 지수분포,exponential_distribution로 유도된다. 첫 번째가 아니고 임의의 n-번째 사건이 발생할 때까지의 시간은 감마분포,gamma_distribution를 따르게 된다.
큰 값과 작은 값의 분포도 매우 유용하다. 예를 들어, 규모가 비슷한 여러 집단이 있을 때 각 집단에서 가장 큰 값만 모아놓은 자료는 검벨분포Gumbel distribution(굼벨_분포,Gumbel_distribution - curr at ![[http]](/123/imgs/http.png) 확률분포)를 따르게 된다. 여기에는 원자료의 확률밀도함수가 큰 값 쪽으로 지수적으로 감소하는 경향을 보여야 한다는 조건이 붙어 있기는 하다.
확률분포)를 따르게 된다. 여기에는 원자료의 확률밀도함수가 큰 값 쪽으로 지수적으로 감소하는 경향을 보여야 한다는 조건이 붙어 있기는 하다.
![[http]](/123/imgs/http.png) 확률분포)를 따르게 된다. 여기에는 원자료의 확률밀도함수가 큰 값 쪽으로 지수적으로 감소하는 경향을 보여야 한다는 조건이 붙어 있기는 하다.
확률분포)를 따르게 된다. 여기에는 원자료의 확률밀도함수가 큰 값 쪽으로 지수적으로 감소하는 경향을 보여야 한다는 조건이 붙어 있기는 하다.이와 반대로 가장 작은 값을 모아놓은 경우는 와이블분포Weibul distribution(sic)(베이불_분포,Weibull_distribution - curr at 확률분포)를 따르게 된다. 이때 자료의 작은 값 쪽으로는 특정 한계가 주어져야 한다. 예를 들어, 1년 중에서 가장 많이 내린 강우자료를 모은 것은 검벨분포로 잘 설명된다. 매월 생산된 부품 중 강도가 가장 작은 것들은 와이블분포로 잘 설명된다.
이 외에도 무수히 많은 확률밀도함수가 존재한다. 이들은 대부분 특정 조건을 가지고 유도된 것들이다. 따라서 어떤 현상을 통계적으로 분석하는 경우 관측된 자료를 가장 잘 설명할 수 있는 확률분포를 선택하는 것은 매우 중요하다. 특히 관측자료의 수가 매우 적을 때에는 더욱 그렇다.
15. Cmts ¶
Excerpt
책 '마스터 알고리즘' 앞부분 챕터 소개
기호주의자symbolists는 학습,learning을 연역,deduction의 역순으로 보며 철학과 심리학, 논리학에서 아이디어를 얻는다.
연결주의자connectionists는 두뇌를 분석하고 모방하며 신경과학과 물리학에서 영감을 얻는다.
진화주의자evolutionaries는 컴퓨터에서 진화를 모의시험하며 유전학과 진화생물학에 의존한다.
베이즈주의자Bayesians는 학습이 확률 추론의 한 형태라고 믿으며 통계학에 뿌리를 둔다.
유추주의자analogizers는 유사성 판단을 근거로 추정하면서 배우며 심리학과 수학적 최적화,optimization의 영향을 받는다. 우리는 머신러닝의 구현 과정을 목적지로 삼아 지난 100년간 일어난 상당한 양의 지적 역사를 두루 확인하며 새로운 각도에서 살펴보는 여행을 떠날 것이다.
책 '마스터 알고리즘' 앞부분 챕터 소개
기호주의자symbolists는 학습,learning을 연역,deduction의 역순으로 보며 철학과 심리학, 논리학에서 아이디어를 얻는다.
연결주의자connectionists는 두뇌를 분석하고 모방하며 신경과학과 물리학에서 영감을 얻는다.
진화주의자evolutionaries는 컴퓨터에서 진화를 모의시험하며 유전학과 진화생물학에 의존한다.
베이즈주의자Bayesians는 학습이 확률 추론의 한 형태라고 믿으며 통계학에 뿌리를 둔다.
유추주의자analogizers는 유사성 판단을 근거로 추정하면서 배우며 심리학과 수학적 최적화,optimization의 영향을 받는다. 우리는 머신러닝의 구현 과정을 목적지로 삼아 지난 100년간 일어난 상당한 양의 지적 역사를 두루 확인하며 새로운 각도에서 살펴보는 여행을 떠날 것이다.
머신러닝의 다섯 종족tribes은 각자 자기만의 마스터 알고리즘master algorithm이 있다. 마스터 알고리즘이란 이론상으로 어느 영역의 데이터에서도 지식을 발견해 내는 범용 학습 알고리즘general-purpose learner이다.
기호주의자의 마스터 알고리즘은 역연역법inverse deduction이고
연결주의자의 마스터 알고리즘은 역전파backpropagation이며
진화주의자의 마스터 알고리즘은 유전자 프로그래밍genetic programming이고
베이즈주의자의 마스터 알고리즘은 베이즈 추정Bayesian inference이며
유추주의자의 마스터 알고리즘은 서포트벡터머신support vector machine이다. 그런데 실제로 각 알고리즘은 특정 작업에는 훌륭하지만 다른 일에는 그렇지 않다. 우리가 진정으로 원하는 것은 다섯 가지 마스터 알고리즘의 핵심 특성을 모두 지닌 단일한 알고리즘, 즉 최종 마스터 알고리즘이다. (중략) 최종 마스터 알고리즘이 머신러닝에서 의미하는 것은 표준 모형standard model이 입자물리학에서 의미하는 것과 같고, 중심 원리central dogma가 분자생물학에서 의미하는 것과 같아서 지금까지 우리가 알고 있는 모든 것을 이해하고 앞으로 수십 년이나 수백 년 동안 이어질 발전의 기반이 되는 통일 이론이다.
기호주의자의 마스터 알고리즘은 역연역법inverse deduction이고
연결주의자의 마스터 알고리즘은 역전파backpropagation이며
진화주의자의 마스터 알고리즘은 유전자 프로그래밍genetic programming이고
베이즈주의자의 마스터 알고리즘은 베이즈 추정Bayesian inference이며
유추주의자의 마스터 알고리즘은 서포트벡터머신support vector machine이다. 그런데 실제로 각 알고리즘은 특정 작업에는 훌륭하지만 다른 일에는 그렇지 않다. 우리가 진정으로 원하는 것은 다섯 가지 마스터 알고리즘의 핵심 특성을 모두 지닌 단일한 알고리즘, 즉 최종 마스터 알고리즘이다. (중략) 최종 마스터 알고리즘이 머신러닝에서 의미하는 것은 표준 모형standard model이 입자물리학에서 의미하는 것과 같고, 중심 원리central dogma가 분자생물학에서 의미하는 것과 같아서 지금까지 우리가 알고 있는 모든 것을 이해하고 앞으로 수십 년이나 수백 년 동안 이어질 발전의 기반이 되는 통일 이론이다.
무한급수 잡다한 사실들 via https://www.youtube.com/watch?v=HUpZswn-uJs
rel. 급수,series 무한급수,infinite_series 멱급수,power_series 테일러_급수,Taylor_series 전개,expansion 테일러_전개,Taylor_expansion
rel. 급수,series 무한급수,infinite_series 멱급수,power_series 테일러_급수,Taylor_series 전개,expansion 테일러_전개,Taylor_expansion
이것의 유도법은 간단한데
(또는, 간단한 암기법은,
모든  에 대해,
에 대해,
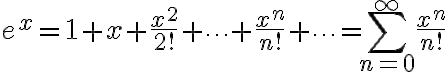
모든  에 대해, ... ( 이하
에 대해, ... ( 이하 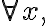 )
)
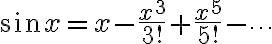
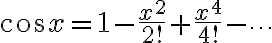
(윗줄 미분하면 아랫줄)
(윗줄 미분하면 아랫줄)
(윗줄 미분하면 아랫줄)
ㅎㅎ -- 163.152.3.162 2022-12-20
t
백분율 percent %  %
%  percent
percent  백분율
백분율  Percentage
Percentage
천분율 permille ‰ ‰
‰  permille
permille  천분율
천분율  Per_mille
Per_mille
만분율 permyriad ‱ ‱
‱  permyriad
permyriad  만분율 - aka basis_point
만분율 - aka basis_point  basis_point
basis_point
...
ppm ppm
ppm
ppb ppb 10억 분의 1
ppb 10억 분의 1
ppt ppt 1조 분의 1
ppt 1조 분의 1
천분율 permille ‰
만분율 permyriad ‱
...
ppm
ppb
ppt
이것들 rel
단위,unit 비,ratio 비율,rate 농도,concentration
백분율,percentage ( 그러고보니 "percent percentage 차이" ? percent percentage 차이
percent percentage 차이  percent percentage 차이 )
percent percentage 차이 )
분수,fraction
퍼센트 기호( 백분율_기호
백분율_기호  Percent_sign ) 모양과 분수의 전체적 모양(대충 한글 '믐, 응' 비슷한) 및
Percent_sign ) 모양과 분수의 전체적 모양(대충 한글 '믐, 응' 비슷한) 및 분수나눗셈 기호(  Division_sign÷ )랑 닮았지만, Wikipedia에 따르면 유래는 아닌 듯...? 숫자 100을 흩뜨려 쓴 것도 아니고. The Italian term per cento, (뜻은 "for a hundred")에서 유래되었다 한다.
Division_sign÷ )랑 닮았지만, Wikipedia에 따르면 유래는 아닌 듯...? 숫자 100을 흩뜨려 쓴 것도 아니고. The Italian term per cento, (뜻은 "for a hundred")에서 유래되었다 한다.  palaeography (=
palaeography (=  paleography , 고문서학)에 따르면 중세-르네상스 시대 알파벳 p의
paleography , 고문서학)에 따르면 중세-르네상스 시대 알파벳 p의  Descender에 가로줄을 친 형태(ꝑ,
Descender에 가로줄을 친 형태(ꝑ,  ꝑ )가 per를 뜻했고, 거기에 cento를 붙인 것이 시대가 흐르면서 변형된 것이 % 기호의 유래라 함.
ꝑ )가 per를 뜻했고, 거기에 cento를 붙인 것이 시대가 흐르면서 변형된 것이 % 기호의 유래라 함.
단위,unit 비,ratio 비율,rate 농도,concentration
백분율,percentage ( 그러고보니 "percent percentage 차이" ?
분수,fraction
퍼센트 기호(
percent point = percentage point ?
 Percentage_point
Percentage_point
 Percentage
Percentage
"A percentage point or percent point is"... 로 시작. 완전 동의어인 듯

