곡선,curve이 휘어진 정도를 실수로 나타낸 것?
곡선의 점에 원,circle을 근사시키는 방법으로 측정. // 근사,approximation라기보다는 접촉,osculation에 가깝지 않나?
그 근사된 원은 곡률원, 그 반지름의 길이는곡률반지름,radius_of_curvature곡률반지름,curvature_radius(w). 곡률은 곡률반지름의 역수,reciprocal.
곡선의 점에 원,circle을 근사시키는 방법으로 측정. // 근사,approximation라기보다는 접촉,osculation에 가깝지 않나?
그 근사된 원은 곡률원, 그 반지름의 길이는
"how fast the function is changing at a given point"[1]
기호: κ, 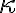 (카파 소문자)
(카파 소문자)
Sub: // 밑에 있는거 여기로 서서히 MV
1. main ¶
곡률을 구하기 전 먼저 접촉원(osculating circle)을 정의, 이것은 기울기,slope를 구할 때의 접선,tangent_line과 비슷한 개념.
(i.e. 곡선의 접점,tangent_point에서의 기울기를 구하려면 먼저 그 접점에서의 접선을 구하는 것과 비슷?)
접촉원의 반지름 (곡률 반지름, 곡률 반지름,radius)일 때 그 역수가 곡률.
(곡률 반지름, 곡률 반지름,radius)일 때 그 역수가 곡률.
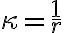
osculate : 접촉하다 (접촉,osculation)
(i.e. 곡선의 접점,tangent_point에서의 기울기를 구하려면 먼저 그 접점에서의 접선을 구하는 것과 비슷?)
접촉원의 반지름
먼저 arclength에 대해 알아야 한다. (See 호길이,arclength - Bazett part)
물론 |=1) 이다.
이다.
곡선 ) 의 곡률
의 곡률 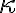 는 r(t)가 이계도함수를 가질 때 다음과 같단다.
는 r(t)가 이계도함수를 가질 때 다음과 같단다.
=\frac{|\vec{r}{}%27{}%27(t)\times\vec{r}{}%27{}%27(t)|}{|\vec{r}{}%27(t)|^3})
이상 p388~
// via (Bazett: How curvy is a curve? Intro to Curvature & Circles of Curvature https://youtu.be/si6ka6HeUdY)
{
매끄러운곡선,smooth_curve에 대한 단위접벡터,unit_tangent_vector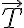 에 대해,
에 대해,
the curvature function κ is given by
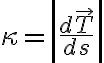
호길이,arclength 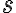 가 아니라 어떤
가 아니라 어떤 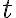 에 대해 매개화된 경우라면 (여기선
에 대해 매개화된 경우라면 (여기선 =\vec{r}%27(t)) 표기를 쓰는 듯)
표기를 쓰는 듯)
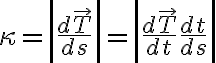
For 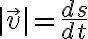

Def. 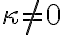 일 때, principal_unit_normal_vector(see 단위법선벡터,unit_normal_vector) for a smooth curve in the plane is
일 때, principal_unit_normal_vector(see 단위법선벡터,unit_normal_vector) for a smooth curve in the plane is
(principal unit normal vector - 주 단위 법선벡터)

Def. circle of curvature (곡률원,curvature_circle)
{
매끄러운곡선,smooth_curve에 대한 단위접벡터,unit_tangent_vector
the curvature function κ is given by
(principal unit normal vector - 주 단위 법선벡터)
- Tangent to the curve at the point
- Same curvature as the curve (i.e. radius = 1/κ)
- Center on the concave (or inner) side
4. Sub: ~곡률 ~curvature ¶
주곡률,principal_curvature 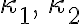 - writing
- writing
법곡률,normal_curvature - writing
가우스_곡률,Gaussian_curvature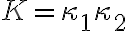 - writing
- writing
) - writing
- writing
측지곡률,geodesic_curvature - w
{
geodesic curvature
법곡률,normal_curvature - writing
가우스_곡률,Gaussian_curvature
Gaussian curvature
 Gaussian_curvature
Gaussian_curvature
https://mathworld.wolfram.com/GaussianCurvature.html
 Pseudosphere
Pseudosphere  Pseudosphere는 a surface with constant negative Gaussian curvature.
Pseudosphere는 a surface with constant negative Gaussian curvature.
평균곡률,mean_curvature https://mathworld.wolfram.com/GaussianCurvature.html
측지곡률,geodesic_curvature - w
{
geodesic curvature
![[https]](/123/imgs/https.png) 수학백과: 측지곡률
수학백과: 측지곡률...
"geodesic curvature"
}
total_geodesic_curvature
전곡률,total_curvature{
total geodesic curvature
전측지곡률 - via total geodesic curvature
total geodesic curvature
"total geodesic curvature"
 total geodesic curvature
total geodesic curvature
Up: 전곡률,total_curvature AND 측지곡률,geodesic_curvature ? CHK
}
total geodesic curvature
전측지곡률 - via
"total geodesic curvature"
Up: 전곡률,total_curvature AND 측지곡률,geodesic_curvature ? CHK
}
{
total curvature
곡선 ) 의 곡률
의 곡률 ) 의 적분
의 적분 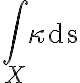 를
를  의 전곡률(total curvature)이라고 한다.
의 전곡률(total curvature)이라고 한다.
(김홍종 미적1+ p360)
(김홍종 미적1+ p360)
6. etc ¶
mklink Frenet-Serret,TNB
Twins:
![[https]](/123/imgs/https.png) 물리학백과: 곡률
물리학백과: 곡률
![[https]](/123/imgs/https.png) 수학백과: 곡률
수학백과: 곡률
 Curvature
Curvature
 곡률
곡률
https://mathworld.wolfram.com/Curvature.html
https://encyclopediaofmath.org/wiki/Curvature
{
목차:
 곡률
곡률
 곡률
곡률
![[https]](/123/imgs/https.png) 물리학백과: 곡률
물리학백과: 곡률![[https]](/123/imgs/https.png) 수학백과: 곡률
수학백과: 곡률https://mathworld.wolfram.com/Curvature.html
https://encyclopediaofmath.org/wiki/Curvature
{
목차:
- 곡선,curve의 곡률
- 곡면,surface의 곡률
- 리만_공간,Riemannian_space{ https://encyclopediaofmath.org/wiki/Riemannian_space }의 곡률
- 부분다양체,submanifold의 곡률

