단조화 운동 (Simple Harmonic Motion)
AKA 단진동, 단순조화운동 (물리학백과)
AKA 단진동, 단순조화운동 (물리학백과)
복원력이 진동 중심에서는 0이고, 진동의 양 끝에서는 최대.
진자의속도속력은 진동 중심에서 최대, 진동의 양 끝에서는 0.
진자의
훅_법칙,Hooke_law을 따르는 계(system)의 진동운동(vibratory motion).
그래프가 sine/cosine을 그리므로 sinusoidal motion이라고도 함.
그래프가 sine/cosine을 그리므로 sinusoidal motion이라고도 함.
1. TOCLEANUP ¶
진동은 안정된 평형점(stable equilibrium) 근처에서 일어난다.
복원력(restoring force): 평형점으로 돌아오도록 작용하는 힘
복원력(restoring force): 평형점으로 돌아오도록 작용하는 힘
작은 진폭일 경우 선형으로 가정할 수 있음.
복원력의 크기가 평형점에서 벗어난 변위에 비례할 때 단조화 운동이 일어난다.: 진폭
: 위상
: 위상상수 (t=0일 때의 위치를 결정)
t=0을 대입해 보라.
한 주기 움직일 때 위상이
먼저 알아둘 것:
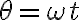
각속도 ω, 반지름 A인 원운동, 시간 t동안 각 θ만큼 회전, 변위 x는
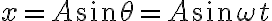
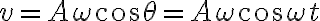
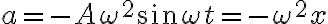
단진동하는 물체 질량이 m이면 작용하는 힘 F는

여기서 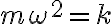 로 놓으면
로 놓으면
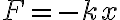 (복원력 형태)
(복원력 형태)
이것을 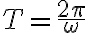 에 대입하면
에 대입하면
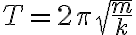
주기는 질량이 클수록, 용수철상수가 작을수록 커짐
위에서
=A\cos(\omega t+\phi))
였는데 이걸 미분하면
=-\omega A\sin(\omega t+\phi))
(위치 함수와 90° 위상차)
또 하면
=-\omega^2 A\cos(\omega t+\phi))
(위치 함수와 180° 위상차)
따라서,
=-\omega^2 x(t))
가 성립.
(위치 함수와 90° 위상차)
(위치 함수와 180° 위상차)
2. 용수철에 매달린 물체의 운동 ¶
훅_법칙,Hooke_law에 의해 (용수철 상수 k)
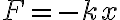
이고, 용수철에 질량 m인 물체가 매달려 있다면
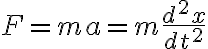
이므로, 물체의 운동방정식은
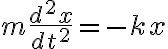
이 되어 물체의 위치 x가 시간 t에 따라 변하는 함수 x(t)를 구하는 문제가 된다.
이것은
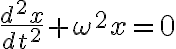
꼴의 미분방정식,differential_equation으로 쓸 수 있고 여기서 오메가(각진동수,angular_frequency)는
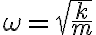
이다. 위 미방의 해는
=A\sin(\omega t+\phi))
즉 조화진동의 운동식은
=A\sin(\omega t+\phi))
여기서 시간 t가 2π/ω만큼 지나면 같은 운동의 양상이 거듭된다. 이 시간이 주기.
이것은
(이상 http://physica.gsnu.ac.kr/ 조화진동 항목 인용)
한 주기를 움직이면 위상이  만큼 증가하므로,
만큼 증가하므로,
+\phi=\omega t+\phi+2\pi)
따라서
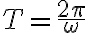
그외
각진동수 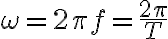
8. Comparing SHM with UCM ¶
College Physics 9e vol1 p.479,
13.3 Comparing Simple Harmonic Motion with Uniform Circular Motion
13.3 Comparing Simple Harmonic Motion with Uniform Circular Motion
curr see 원운동,circular_motion
9. 참고 links ko ¶
일반물리 SHM 요약
1 https://mathphysics.tistory.com/157
2 https://mathphysics.tistory.com/158 등속원운동과의 비교 및 진자
3 https://mathphysics.tistory.com/164 감쇠진동
1 https://mathphysics.tistory.com/157
2 https://mathphysics.tistory.com/158 등속원운동과의 비교 및 진자
3 https://mathphysics.tistory.com/164 감쇠진동


![[https]](/123/imgs/https.png)