∇,  또는
또는 
벡터미적분,vector_calculus에서 쓰이는 기호.
정의
)
이거 맞나 CHK
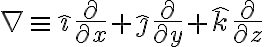
i,j,k를 오른쪽에 쓸 수도 있지만, 이렇게 왼쪽으로 쓰는 게 더 좋아 보임. 왜냐면 기울기,gradient를 표현할 때 대상을 바로 이렇게 오른쪽에 쓸 수 있기 때문 (중요한 건 아니지만)

i,j,k를 오른쪽에 쓸 수도 있지만, 이렇게 왼쪽으로 쓰는 게 더 좋아 보임. 왜냐면 기울기,gradient를 표현할 때 대상을 바로 이렇게 오른쪽에 쓸 수 있기 때문 (중요한 건 아니지만)
3차원 공간에서만? - No, n차원에서 정의 가능. 다음과 같이.
)
기하학적으로, 각 (축,axis이나 기저,basis)에 대한 편미분,partial_derivative 연산자로 만든 벡터,vector??? CHK
AKA gradient operator
직각좌표계에서
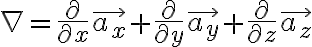
원통좌표계에서
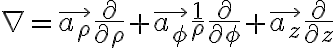
구좌표계에서
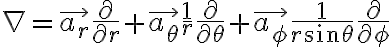
(Sadiku 식 3.16, 3.19, 3.23)
Properties ¶
tmp: 여러 좌표계에서 ¶
ysi (전자기학) ¶
tmp: 비교: 위치벡터와 디퍼렌셜과 델 ¶
위치벡터,position_vector
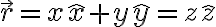
미분,differential
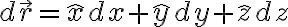
델 연산자
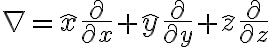
델 연산자의 정의:
 \cdot d\vec{r})
// from 차동우 https://youtu.be/IAIADoy83as?t=470 나머지 나중에 tbw
RENAMETHISPAGE to del_operator? or just nabla?
AKA 
Twins:
 델_(연산자)
델_(연산자)
 Del
Del
 델(연산자)
델(연산자)
https://ncatlab.org/nlab/show/nabla - AKA atled (delta의 철자를 거꾸로 한 것. ohm ↔ mho 와 비슷?)
 del operator
del operator
https://ncatlab.org/nlab/show/nabla - AKA atled (delta의 철자를 거꾸로 한 것. ohm ↔ mho 와 비슷?)


![[http]](/123/imgs/http.png)