미분,differentiation은 도함수(derivative)를 찾는 행동.
도함수를 찾기 전단계의 함수가 원시함수. 원시함수는 하나만 존재하지 않고 임의의 상수를 더한(상수의 차이) 만큼만 다른 무한개가 있음. 즉 임의의 두 원시함수의 차이는 상수만큼임. - 관련: 적분,integration
Sub:
see also 로그함수,logarithmic_function#s-4
rel. Logarithmic_differentiation
Logarithmic_differentiation
 Logarithmic_derivative
Logarithmic_derivative
}
일계도함수  first_derivative
first_derivative
 second_derivative
second_derivative
 이계도함수
이계도함수
 Second_derivative
Second_derivative
https://proofwiki.org/wiki/Definition:Second_Derivative
(ex. 가속도,acceleration는 시간에 대한 변위,displacement의 이계도함수, 속도,velocity의 일계도함수.)
편미분,partial_derivative
방향도함수,directional_derivative
전미분,total_derivative
logarithmic_derivative 로그미분 or 로그도함수
{(ex. 속도,velocity는 시간에 대한 변위,displacement의 일계도함수.)
https://proofwiki.org/wiki/Definition:First_Derivative
이계도함수 https://proofwiki.org/wiki/Definition:First_Derivative
https://proofwiki.org/wiki/Definition:Second_Derivative
(ex. 가속도,acceleration는 시간에 대한 변위,displacement의 이계도함수, 속도,velocity의 일계도함수.)
방향도함수,directional_derivative
전미분,total_derivative
logarithmic_derivative 로그미분 or 로그도함수
see also 로그함수,logarithmic_function#s-4
rel.
}
functional_derivative
Radon-Nikodym_derivative - writing
도함수의 일반화 -  Generalizations_of_the_derivative
Generalizations_of_the_derivative
ex.
subderivative - 볼록해석,convex_analysis 쪽에서 사용하는 derivative의 일반화? curr at subgradient
subgradient
weak_derivative - 약도함수
약도함수  Weak_derivative
Weak_derivative
범함수미분? 범함수도함수? // (tmp) kms functional derivative => https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=functional derivative
도함수(=미분,derivative)의 일반화. 변분법,variational_calculus에 등장. 여기선 함수,function를 변수,variable에 대해 미분,differentiation하는 대신에, 범함수,functional를 함수,function에 대해 미분한다. (MW)
https://mathworld.wolfram.com/FunctionalDerivative.html
https://ncatlab.org/nlab/show/functional derivative
 Functional_derivative
Functional_derivative
… functional derivative
functional derivative
Frechet_derivative도함수(=미분,derivative)의 일반화. 변분법,variational_calculus에 등장. 여기선 함수,function를 변수,variable에 대해 미분,differentiation하는 대신에, 범함수,functional를 함수,function에 대해 미분한다. (MW)
https://mathworld.wolfram.com/FunctionalDerivative.html
https://ncatlab.org/nlab/show/functional derivative
…
프레셰_도함수?
Fréchet derivative
전미분,total_derivative을 바나흐_공간,Banach_space = complete_normed_space 로 일반화한 것.
https://freshrimpsushi.github.io/posts/frechet-derivative/
 프레셰_도함수
프레셰_도함수
https://encyclopediaofmath.org/wiki/Fréchet_derivative - strong derivative
https://mathworld.wolfram.com/FrechetDerivative.html
https://ncatlab.org/nlab/show/Fréchet derivative
… frechet derivative
frechet derivative
Gateaux_derivativeFréchet derivative
전미분,total_derivative을 바나흐_공간,Banach_space = complete_normed_space 로 일반화한 것.
https://freshrimpsushi.github.io/posts/frechet-derivative/
https://encyclopediaofmath.org/wiki/Fréchet_derivative - strong derivative
https://mathworld.wolfram.com/FrechetDerivative.html
https://ncatlab.org/nlab/show/Fréchet derivative
…
Gâteaux derivative
가토 도함수 via https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=gateaux
방향도함수,directional_derivative의 일반화? chk
https://mathworld.wolfram.com/GateauxDerivative.html
https://encyclopediaofmath.org/wiki/Gâteaux_derivative - weak derivative
… gateaux derivative
gateaux derivative
위 둘 {Gateaux, Frechet} derivative에 대한 한국어 글 - https://elementary-physics.tistory.com/52가토 도함수 via https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=gateaux
방향도함수,directional_derivative의 일반화? chk
https://mathworld.wolfram.com/GateauxDerivative.html
https://encyclopediaofmath.org/wiki/Gâteaux_derivative - weak derivative
…
Radon-Nikodym_derivative - writing
ex.
subderivative - 볼록해석,convex_analysis 쪽에서 사용하는 derivative의 일반화? curr at
weak_derivative -
1. 고계도함수 (high order derivatives) ¶
...
1.2. 이계도함수 second derivative, second order derivative ¶
![[https]](/123/imgs/https.png) 수학백과: 이계도함수
수학백과: 이계도함수당연히...뻔한얘기 함. 다음과의 관계.
가속도,acceleration
오목볼록,concave_and_convex
극점 { 극값,extremum 극점,extreme_point or 극점,extremal_point : 극대,local_maximum 극소,local_minimum 극대점 극소점 극대값 극소값 ...? }
rel.오목볼록,concave_and_convex
극점 { 극값,extremum 극점,extreme_point or 극점,extremal_point : 극대,local_maximum 극소,local_minimum 극대점 극소점 극대값 극소값 ...? }
이계도함수판정법,second_derivative_test
2. 미분공식들 ¶
상수함수의 도함수는 0
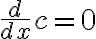
항등함수의 도함수는 1
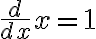
지수함수,exponential_function의 도함수는 자기 꼴이 그대로 포함

로그함수,logarithmic_function의 도함수는 분수 형태
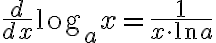
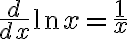
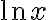 와
와 ) 의 도함수가 같음
의 도함수가 같음

, \quad y%27 = \frac{(-x)%27}{-x} = \frac1x\right))
곱의 미분법(두 함수의 곱의 미분법)의 다른 이름은 라이프니츠 정리, 라이프니츠 법칙.
![[https]](/123/imgs/https.png) 수학백과: 라이프니츠 정리
수학백과: 라이프니츠 정리
이 식을 적분하면 바로 부분적분,integration_by_parts방법이 됨.
Derivative Product Rule:
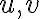 가
가  에서 미분가능하면
에서 미분가능하면 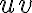 도 미분가능하며
도 미분가능하며
=u\frac{dv}{dx}+v\frac{du}{dx})
%27=uv%27+vu%27) (in prime notation)
(in prime notation)
![$\frac{d}{dx}[f(x)g(x)]=f(x)g'(x)+g(x)f'(x)$ $\frac{d}{dx}[f(x)g(x)]=f(x)g'(x)+g(x)f'(x)$](/123/cgi-bin/mimetex.cgi?\Large \frac{d}{dx}[f(x)g(x)]=f(x)g%27(x)+g(x)f%27(x)) (in function notation)
(in function notation)
(Thomas 11e)
![[https]](/123/imgs/https.png) 수학백과: 라이프니츠 정리
수학백과: 라이프니츠 정리이 식을 적분하면 바로 부분적분,integration_by_parts방법이 됨.
Derivative Product Rule:
몫의 미분법(두 함수의 분수 꼴의 미분법)
![[https]](/123/imgs/https.png) 수학백과: 몫의 미분법
수학백과: 몫의 미분법
Derivative Quitient Rule
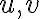 가
가  에서 미분가능하고
에서 미분가능하고 \ne 0) 이면 몫,quotient
이면 몫,quotient 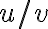 도
도  에서 미분가능하며
에서 미분가능하며
=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2})
![$\frac{d}{dx}\left[\frac{f(x)}{g(x)}\right]=\frac{g(x)f'(x)-f(x)g'(x)}{g^2(x)}$ $\frac{d}{dx}\left[\frac{f(x)}{g(x)}\right]=\frac{g(x)f'(x)-f(x)g'(x)}{g^2(x)}$](/123/cgi-bin/mimetex.cgi?\Large \frac{d}{dx}\left[\frac{f(x)}{g(x)}\right]=\frac{g(x)f%27(x)-f(x)g%27(x)}{g^2(x)}) (in function notation)
(in function notation)
(Thomas 11e)
![[https]](/123/imgs/https.png) 수학백과: 몫의 미분법
수학백과: 몫의 미분법Derivative Quitient Rule
매개변수로 표현된 함수의 미분법
,\;y=g(t)) 일 때
일 때
}{f%27(t)})
역함수의 미분법
) 가 미분 가능하고
가 미분 가능하고 =b) 일 때
일 때
%27(b)=\frac{1}{f%27(f^{-1}(b))}=\frac{1}{f%27(a)})
CHK WHY
......
역함수,inverse_function의 도함수
{
함수 가 미분가능하고 역함수
가 미분가능하고 역함수 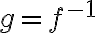 를 가지면,
를 가지면,
![$\frac{d}{dx}\left[f^{-1}(x)\right]=g'(x)=\frac1{f'(g(x))$ $\frac{d}{dx}\left[f^{-1}(x)\right]=g'(x)=\frac1{f'(g(x))$](/123/cgi-bin/mimetex.cgi?\Large \frac{d}{dx}\left[f^{-1}(x)\right]=g%27(x)=\frac1{f%27(g(x)))
증명:  역함수의_도함수(미분)_증명
역함수의_도함수(미분)_증명
}
tmp from https://blog.naver.com/dydrogud22/110189290591 맨아래
{
)=x,\;g(x)=f^{-1}(x)) 이고 기타 미분가능 등 조건들 성립하면
이고 기타 미분가능 등 조건들 성립하면
)=\frac{d}{dx}x)
)g%27(x)=1)
)\ne0) 이면,
이면,
=\frac{1}{f%27(g(x))})
%27(x)=\frac{1}{f%27(f^{-1}(x))})
}
......
역함수,inverse_function의 도함수
{
함수
단, )\ne 0)
}
tmp from https://blog.naver.com/dydrogud22/110189290591 맨아래
{
3. 미분(derivative)의 표기법, 도함수의 표기법 ¶
Lagrange
 에 대해 미분할 때,
에 대해 미분할 때,
1계미분: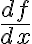
2계미분: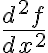
n계미분: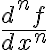
(Lagrange 표기법에 비해서: 번거롭다는 단점, 종속변수,dependent_variable가 명확하게 나타난다는 장점.)
Newton
Euler
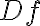
첨자 표기법 subscript notation?
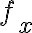
편미분의 경우 어떤 변수에 대해 미분하는지가 중요하므로 Leibniz표기법과 첨자표기법이 주로 쓰이며 Leibniz표기법의 경우 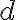 자리에
자리에 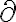 을 쓴다. See 편미분,partial_derivative#s-1
을 쓴다. See 편미분,partial_derivative#s-1
1계미분: 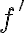
2계미분: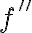
n계미분:})
Leibniz2계미분:
n계미분:
1계미분:
2계미분:
n계미분:
(Lagrange 표기법에 비해서: 번거롭다는 단점, 종속변수,dependent_variable가 명확하게 나타난다는 장점.)
Euler
Up: 미적분,calculus, esp. differential calculus
Related: 영단어 derivative는 미적분학·해석학에서 주로 미분·도함수로 번역되며 그 외에선 대개 유도,derivation로 번역됨.
Twins:
 미분,derivative
미분,derivative
https://planetmath.org/derivative
https://mathworld.wolfram.com/Derivative.html
https://ncatlab.org/nlab/show/derivative
https://planetmath.org/derivative
https://mathworld.wolfram.com/Derivative.html
https://ncatlab.org/nlab/show/derivative

