Sub:
{
유형에 따른 분류
상미분방정식,ordinary_differential_equation,ODE
편미분방정식,partial_differential_equation,PDE ...등등 분류는 아래 section 1에 있는데 서서히 여기로 mv.
완전미분방정식,exact_differential_equation
자율미분방정식,autonomous_differential_equation
확률미분방정식,stochastic_differential_equation
초기값문제,initial_value_problem,IVP - writing
경계값문제,boundary_value_problem,BVP - writing
각각 다음과 대응? chk
초기조건,initial_condition
경계조건,boundary_condition
tmp편미분방정식,partial_differential_equation,PDE ...등등 분류는 아래 section 1에 있는데 서서히 여기로 mv.
완전미분방정식,exact_differential_equation
자율미분방정식,autonomous_differential_equation
확률미분방정식,stochastic_differential_equation
초기값문제,initial_value_problem,IVP - writing
경계값문제,boundary_value_problem,BVP - writing
각각 다음과 대응? chk
초기조건,initial_condition
경계조건,boundary_condition
{
유형에 따른 분류
독립변수,independent_variable 개수에 따라
- 상미분방정식 : 독립변수가 1개
- 편미분방정식 : 독립변수가 2개 이상
first-order_ordinary_differential_equation first-order_ODE
first-order ordinary differential equation
https://mathworld.wolfram.com/First-OrderOrdinaryDifferentialEquation.html
https://mathworld.wolfram.com/First-OrderOrdinaryDifferentialEquation.html
https://everything2.com/title/linear differential equation
{
linear_first-order
linear_second-order
- 종속변수
와 그것의 모든 도함수들
은 1차이다. 즉
를 포함하는 각각의 항들은 1차 거듭제곱이다.
의 계수함수
들은 독립변수
만의 함수이다.
비선형 상미분방정식에는 '비선형 항'이 있어서 구별할 수 있는 듯.
비선형 상미분방정식의 예와 그 방정식이 비선형인 이유 example. (Zill)
}
비선형 상미분방정식의 예와 그 방정식이 비선형인 이유 example. (Zill)
| 비선형 ODE | 비선형 항 | 설명 |
| 거듭제곱이 1이 아님 .... // 참고로, |
rel. 초기하급수,hypergeometric_series-writing
https://encyclopediaofmath.org/wiki/Hypergeometric_equation - Gauss equation
http://mathonline.wikidot.com/differential-equations - good, 정리 + 간단한 예제https://encyclopediaofmath.org/wiki/Hypergeometric_equation - Gauss equation
2nd order ODE.
tmp
{
검색으로 나온
knu 2011-2 미분방정식 시험 3 pdf => http://bh.knu.ac.kr/~ilrhee/lecture/exam/2011-2-mibun-exam3-ans.pdf
URL에서
http://bh.knu.ac.kr/~ilrhee/
경북대 이일수 교수(물리) 홈페이지. 일반물리 / 현대물리 / 미분방정식 / 전자회로 강의 자료 있음.
}
{
검색으로 나온
knu 2011-2 미분방정식 시험 3 pdf => http://bh.knu.ac.kr/~ilrhee/lecture/exam/2011-2-mibun-exam3-ans.pdf
URL에서
http://bh.knu.ac.kr/~ilrhee/
경북대 이일수 교수(물리) 홈페이지. 일반물리 / 현대물리 / 미분방정식 / 전자회로 강의 자료 있음.
}
}
Sub:
{
미방 해결 기술들 techniques:
{
미방 해결 기술들 techniques:
미정계수법 method_of_undetermined_coefficients
writing
writing
ㅁㅁ감소법? (order를 뭘로 번역하느냐에 따라 계수감소법 or 차수감소법, 근데 계수는 coefficient랑 번역이 겹치고..) reduction_of_order order_reduction
writing
writing
매개변수변환법(번역은 wpko) variation_of_parameters
writing
writing
프로베니우스 방법/해법
Frobenius_method
특정 종류의 linear ODE를 멱급수전개,power_series_expansion로 푸는 방법
 프로베니우스_방법
프로베니우스_방법
 Frobenius_method
Frobenius_method
Frobenius_method
특정 종류의 linear ODE를 멱급수전개,power_series_expansion로 푸는 방법
}
Contents
미지함수의 도함수(미분,derivative)를 포함하는 방정식
ex.
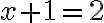 의 해는 수 하나
의 해는 수 하나
... 의 해는 두 수
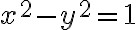 의 해는 두 수 (수의 순서쌍)의 집합
의 해는 두 수 (수의 순서쌍)의 집합
=f(x)) 의 해는 함수
의 해는 함수 =Ce^x) (의 집합?)
(의 집합?)
다음 항상 옳은지 CHK
(page links: 방정식,equation, 미분,differential, 차분,difference=차이,difference, 차분방정식,difference_equation, 수,number, 함수,function, 수열,sequence)
... 의 해는 두 수
| 해,solution | |
| 그냥 방정식 | 숫자 |
| 미분 방정식 | 함수 |
| 차분 방정식 | 수열 |
종속변수 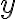 의 도함수를 포함하는 방정식, 즉
의 도함수를 포함하는 방정식, 즉 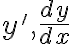 등을 포함하는 방정식
등을 포함하는 방정식
하나 이상의 독립변수에 대해, 하나 이상의 종속변수의 도함수(derivative)를 포함하는 방정식
(See also 독립변수와_종속변수)
종속변수를 독립변수에 대해 미분한 도함수를 포함하는 방정식
하나 이상의 독립변수에 대해, 하나 이상의 종속변수의 도함수(derivative)를 포함하는 방정식
(See also 독립변수와_종속변수)
종속변수를 독립변수에 대해 미분한 도함수를 포함하는 방정식
미분이란 변화율이고,
미분방정식이란 변화율의 방정식
미분방정식이란 변화율의 방정식
풀 때
방향장,direction_field과 integral curve(적분 곡선, 해곡선)
를 그리기도 한다. 해의 정성적인 성질을 파악할 수 있다. 구체적인 해를 구하기는 힘들다.
방향장,direction_field과 integral curve(적분 곡선, 해곡선)
를 그리기도 한다. 해의 정성적인 성질을 파악할 수 있다. 구체적인 해를 구하기는 힘들다.
1. 미분방정식의 분류 ¶
상미방: 독립변수가 하나인 미분방정식
편미방: 독립변수가 둘 이상인 미분방정식
편미방: 독립변수가 둘 이상인 미분방정식
선형미방: 종속변수가 1차인 항만으로 구성된 미방
비선형미방: 종속변수가 2차 이상인 항이 하나라도 포함된 미방
비선형미방: 종속변수가 2차 이상인 항이 하나라도 포함된 미방
제차미방: 독립변수만으로 된 항이 없는 미방
비제차미방: 독립변수만으로 된 항이 포함된 미방
비제차미방: 독립변수만으로 된 항이 포함된 미방
1.1. 계수, 차수, m계 n차 ¶
| 계수 | order | 최대 미분 횟수. 방정식에 나타난 최대 미분 수. 미분방정식에 나타난 가장 높은 미분 횟수. |
| 차수 | degree | 계수가 가장 높은 도함수의 거듭제곱수. |
예
종속변수(보통 y) 차수(degree)가 1차이면 선형, 아니면 비선형.
| 2계 1차 | |
| 2계 3차 | |
| 2계 1차 |
종속변수(보통 y) 차수(degree)가 1차이면 선형, 아니면 비선형.
1.2. form (Zill) ¶
n계 미방의 general form:
})=0)
n계 미방의 normal form:
}))
즉, 1계 미방의 normal form:
)
2계 미방의 normal form:
)
즉, 1계 미방의 normal form:
1.4. 상미분방정식(ODE)과 편미분방정식(PDE) ¶
편미분방정식,partial_differential_equation,PDE
독립 변수 2개 이상
종속 변수 1개 이상
두 개 이상의 독립변수에 대한 도함수(편미분)을 포함하는 방정식
독립 변수 2개 이상
종속 변수 1개 이상
두 개 이상의 독립변수에 대한 도함수(편미분)을 포함하는 방정식
편미방 중에서,
선형 편미방: 풀고자 하는 함수의 편도함수들과 함수의 차수가 모두 1차
비선형 편미방: 그렇지 않은 경우
비선형 편미방: 그렇지 않은 경우
1.5. 제차(homogeneous), 비제차(nonhomogeneous) 미분방정식 ¶
Homogeneous가 아니면 inhomogeneous.
Ex.
1.6. 선형/비선형 ¶
선형성,linearity 유무에 따라, 선형linear/비선형nonlinear 미분방정식으로 나눔.
선형미분방정식: 종속변수와 그 도함수가 모두 1차인 미방
비선형미분방정식: 선형이 아닌 경우
비선형미분방정식: 선형이 아닌 경우
선형미분방정식: }) 에 대해 선형
에 대해 선형
즉 y^{(n)}+a_{n-1}(x)y^{(n-1)}+\cdots+a_1(x)y%27+a_0(x)y=g(x)) 꼴
꼴
비선형 미분방정식: 선형이 아닌 방정식선형이 되기 위해서는 y와 그 도함수가 1차이어야 하며 그 계수가 독립변수에만 의존해야 한다.
linearity: linear한 미분방정식은,
y^{(n)}+a_{n-1}(x)y^{(n-1)}+\cdots+a_1(x)y%27+a_0(x)y=g(x))
특히, 다음 두 가지가 중요
linearity: linear한 미분방정식은,
linear first-order (n=1)
\frac{dy}{dx}+a_0(x)y=g(x))
) 로 나누면 다음 standard form이 된다.
로 나누면 다음 standard form이 된다.
y=f(x))
linear second-order (n=2)
\frac{d^2y}{dx^2}+a_1(x)\frac{dy}{dx}+a_0(x)y=g(x))
linear하지 않으면 nonlinear.여기서 =0) 이면 homogeneous, 아니면 nonhomogeneous.
이면 homogeneous, 아니면 nonhomogeneous.
양변을 3. 해 (solution) ¶
해,solution(writing)
미분방정식의 해 (solution) : 미분방정식에 대입하면 방정식이 만족되는 것. 함수임. 함수를 미분방정식에 대입하여 (QQQ: 어떤 구간의 모든 점에 대해? 항상 이런 조건? CHK - Stewart 미방 소개 앞부분.) 만족하면 해.
미분방정식의 해 (solution) : 미분방정식에 대입하면 방정식이 만족되는 것. 함수임. 함수를 미분방정식에 대입하여 (QQQ: 어떤 구간의 모든 점에 대해? 항상 이런 조건? CHK - Stewart 미방 소개 앞부분.) 만족하면 해.
해가 '값'인 그냥 방정식과는 달리, 미분방정식은 해가 '함수' 꼴이므로, 이걸로 곡선,curve 그래프를 그릴 수 있다. 해곡선(solution curve)을 그릴 수 있다. CHK // 해곡선,solution_curve
특수해 (particular solution) : 임의의 상수(? 일반해에 나오는 적분상수?)에 특정한 값을 대입한 해
특이해 (singular solution) :특수해가 아닌 해
특수해,particular_solution
특이해,singular_solution
어떤 경우에 해당?
해곡면 뭐 이런 건 없나?
일반해 (general solution) : 계수만큼 상수를 가진 해해곡면 뭐 이런 건 없나?
특수해 (particular solution) : 임의의 상수(? 일반해에 나오는 적분상수?)에 특정한 값을 대입한 해
특이해 (singular solution) :
보통 일반해 형태로 나타낼 수 없는 경우를 특이해라 하고, 그 외의 의미는 해가 특이점,singularity을 갖는 경우와 해의 유일성,uniqueness이 성립하지 않는 경우의 해를 뜻한다고 함. [2]
일반해,general_solution특수해,particular_solution
특이해,singular_solution
trivial solution
{
미분방정식의 일반해는 (대체로?) 무한 개의 해를 가질 수 있다... 그래서
암튼 별 의미는 없을것같은데, 일반적으로 어떤 DE의 해의 개수? (cardinality 연산자 써서)로 따지면 |일반해의집합| > |특수해의집합|
자명해,trivial_solution는 일반적으로 별 쓸모가 없는듯??? why?
자명해?
대충내생각, not sure, chk{
미분방정식의 일반해는 (대체로?) 무한 개의 해를 가질 수 있다... 그래서
암튼 별 의미는 없을것같은데, 일반적으로 어떤 DE의 해의 개수? (cardinality 연산자 써서)로 따지면 |일반해의집합| > |특수해의집합|
자명해,trivial_solution는 일반적으로 별 쓸모가 없는듯??? why?
일반해 : 어떤 (매개변수?)가 아직 정의되지 않고 적분상수처럼 있는, 그래서 경우가 너무 많은, 그런 경우
특수해 : particular. 그것이 특정 값으로 확정/특정되어 해가 특정하게 정해진 그런 경우
특이해 : singular. (어떤 매개변수를 택해도 안 되는, 매개변수로 표현을 할 수 없는)
자명해 : 뻔하고 간단하지만 (대체로) 쓸모는 없는 그런 해
특수해 : particular. 그것이 특정 값으로 확정/특정되어 해가 특정하게 정해진 그런 경우
특이해 : singular. (어떤 매개변수를 택해도 안 되는, 매개변수로 표현을 할 수 없는)
자명해 : 뻔하고 간단하지만 (대체로) 쓸모는 없는 그런 해
trivial_solution 은 왠지 (방정식 등의) degenerate_case 와 관련이 있나? 그럴 것 같은 느낌
}
}
explicit solution: ) ex.
ex. 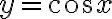
implicit solution:=0) ex.
ex. )
implicit solution:
general solution: 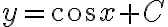
particular solution: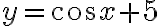
particular solution:
initial solution이 주어져 있어서 C를 구할 수 있는 경우
singular solution: a solution that cannot be expressed by the general solution3.1. 해의 종류 ¶
일반해(general solution)
특수해(particular solution)
특이해(singular solution)
자명해(trivial solution)
특수해(particular solution)
특이해(singular solution)
자명해(trivial solution)
chk
{
특수해: 해곡선 solution_curve
일반해: 해곡선의 집합
}
{
특수해: 해곡선 solution_curve
일반해: 해곡선의 집합
}
3.3. 미분방정식의 해 ¶
주어진 미분방정식을 만족하는 독립변수와_종속변수 사이의 관계를 얻었을 때 그 관계(방정식)를 미분방정식의 해라고 한다.
![[https]](/123/imgs/https.png) src 권태원
src 권태원
- 일반해 : 임의의 상수를 포함하는 해
- 특수해 : 일반해의 상수가 조건을 만족하는 해
- 특이해 : 미분방정식을 풀어서 구할 수 없는 해
![[https]](/123/imgs/https.png) src 권태원
src 권태원5.3. 빗방울의 낙하 ¶
시각 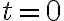 일 때 떨어지기 시작하면, 시각
일 때 떨어지기 시작하면, 시각 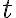 일 때 속도
일 때 속도 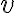 는?
는?
빗방울에 작용하는 힘,force은 아래쪽으로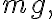 위쪽으로 저항력
위쪽으로 저항력 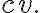
그래서 지구 방향으로 잡아당기는 힘은
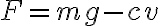
그리고 이것이 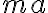 이므로
이므로
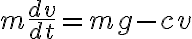
양변을 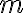 으로 나누면
으로 나누면
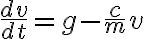 (← 미분방정식)
(← 미분방정식)
=0)
풀면
)
Ref. 10개의 특강으로 끝내는 수학의 기본 원리
빗방울에 작용하는 힘,force은 아래쪽으로
그래서 지구 방향으로 잡아당기는 힘은
5.4. Population ¶
Exponential growth model.
박테리아의 개체수(population)를 P라 하고, 영양분과 공간이 충분하다고 가정할 때, 성장률(비율,rate of growth)은 개체수에 비례한다.
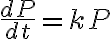
이것의 답은
=Ce^{kt})
박테리아의 개체수(population)를 P라 하고, 영양분과 공간이 충분하다고 가정할 때, 성장률(비율,rate of growth)은 개체수에 비례한다.
5.5. 예제: RC회로 ¶
RC회로,RC_circuit
from 차동우 대학물리 p100
일단
=\frac{dq(t)}{dt})
RC회로에 키르히호프의 고리법칙을 적용하면
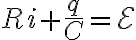

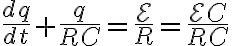
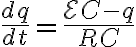
1차 미분방정식이므로 항상 적분에 의해 풀 수 있다.
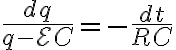
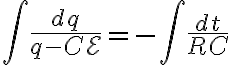
시간 0~t에 대해 적분한다면 전하에 대해서는 q(0)~q(t)까지 적분하여야 한다.
}^{q(t)}\frac{dq}{q-C\mathcal{E}}=-\int_0^{t}\frac{dt}{RC})
(q(0)=q0, q(t)=q로 책에는 표기)
우변은 -t/RC이고 좌변은
}^{q(t)}\frac{d(q-C\mathcal{E})}{q-C\mathcal{E}}=\ln(q-C\mathcal{E})|_{q(0)}^{q(t)}=\ln\frac{q(t)-C\mathcal{E}}{q(0)-C\mathcal{E}})
따라서,
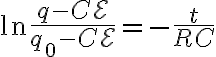
e^{-t/RC})
=C\mathcal{E}(1-e^{-t/RC})+q_0e^{-t/RC})
대부분 스위치를 닫는 순간에는 축전기에 대전된 전하가 q0=0인 경우가 많으며 그런 경우엔
=C\mathcal{E}\left(1-e^{-t/RC}\right))
i(t)는 전하를 시간으로 미분하면 구할 수 있으므로
=\frac{d}{dt}q(t)=\frac{d}{dt}C\mathcal{E}(1-e^{-t/RC})=\frac{\mathcal{E}}{R}e^{-\frac{t}{RC}})
q-t 그래프: 0에서 시작, Cℰ까지 증가 (점근)
i-t 그래프: ℰ/R에서부터 감소, 0까지 점근
from 차동우 대학물리 p100
일단
우변은 -t/RC이고 좌변은
i-t 그래프: ℰ/R에서부터 감소, 0까지 점근
5.6. Examples from 최정환 ¶
CHK:
linear DE: y, y', ... 이것들이 선형결합한것
nonlinear DE: yy' 같은 항들이 있는것
linear DE: y, y', ... 이것들이 선형결합한것
nonlinear DE: yy' 같은 항들이 있는것
homogeneousness:
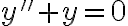
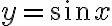 is a solution;
is a solution; 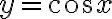 is also a solution.
is also a solution.
2.
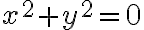 is a solution of
is a solution of 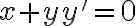
(naver 어학사전: 같은 종류의 것으로 됨; 동일 조직임)
F(y, …, y(n), x) = 0에서 x만으로 된 항,term이 등장하지 않으면 homogeneous하다.
x만으로 된 term이 등장하면 inhomogeneous.
1.F(y, …, y(n), x) = 0에서 x만으로 된 항,term이 등장하지 않으면 homogeneous하다.
x만으로 된 term이 등장하면 inhomogeneous.
12.1. natural growth/decay ¶
시각 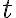 에서 수량이
에서 수량이 ) 이고,
이고, 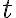 에 관한
에 관한 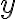 의 변화율이 항상(임의의 시각에서)
의 변화율이 항상(임의의 시각에서) ) 에 비례한다면,
에 비례한다면,
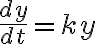
여기서  는 상수이고,
는 상수이고,
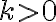 : law of natural growth
: law of natural growth
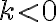 : law of natural decay
: law of natural decay
12.3. Excerpt: 김홍종 미적1+ ¶
(미방에 대한 intro)
방사능 물질 붕괴 - 매 순간 붕괴하는 양은 현재의 질량에 비례하여 나타나므로
=-km(t))
같은 미분방정식으로 나타나고, 은행에 예금한 돈에 이자가 붙어 늘어나는 것은 // 현재 돈에 비례하므로
=+ka(t))
같은 식으로 나타난다. 이와 같이 어떤 함수  와 그 도함수
와 그 도함수 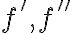 등이 어떤 관계식
등이 어떤 관계식
,f%27(t),f%27%27(t),\cdots)=0)
으로 표현될 때, 이 식을 미분방정식이라 부르고, 이러한 식을 만족시키는 함수 ) 를 구하는 것을 '미분방정식을 푼다'고 말한다.
를 구하는 것을 '미분방정식을 푼다'고 말한다.
방사능 물질 붕괴 - 매 순간 붕괴하는 양은 현재의 질량에 비례하여 나타나므로
두번째 식을 풀어 보자. 물론 이 식을 만족시키는 함수 ) 는 미분가능함수,differentiable_function이고, 따라서 연속함수,continuous_function라야 할 것이다.
는 미분가능함수,differentiable_function이고, 따라서 연속함수,continuous_function라야 할 것이다.
그런데) 의 도함수
의 도함수 ) 가
가 ) 이므로,
이므로, ) 는 연속함수이다.
는 연속함수이다.
이와 같이 도함수가 연속인 함수를 일급미분가능함수(differentiable function of class 𝒞1) 또는 줄여서 일급함수(𝒞1 함수)라고 부른다.
한편) 가 일급함수
가 일급함수 ) 와 같으므로,
와 같으므로, ) 는 또 다시 미분가능하고
는 또 다시 미분가능하고
=ka%27(t)=k^2a(t))
이므로 ) 는 이급함수(𝒞2 함수)이다. 이와 같이 처음에 주어진 관계식에서 새로운 관계식
는 이급함수(𝒞2 함수)이다. 이와 같이 처음에 주어진 관계식에서 새로운 관계식
}(t)=k^n a(t) \;\;\; (n=0,1,2,3,\ldots))
가 얻어지고, 이로부터 미분방정식의 해는, 만약 존재한다면, 무한급 함수 즉 𝒞∞ 함수라는 것을 알 수 있다. 그러므로 처음에 예금한 금액을 =:a_0) 라고 하면,
라고 하면,
}(0)=k^n a_0)
이고, 따라서 ) 가 거듭제곱급수(=멱급수,power_series) 함수라면
가 거듭제곱급수(=멱급수,power_series) 함수라면
:=\sum_{n=0}^{\infty} \frac{k^n a_0}{n!} t^n = a_0 e^{kt})
이라야 함을 알 수 있다.
그런데
이와 같이 도함수가 연속인 함수를 일급미분가능함수(differentiable function of class 𝒞1) 또는 줄여서 일급함수(𝒞1 함수)라고 부른다.
한편
이제 초기 조건이 주어진 미분방정식 // initial_value_problem
=ka(t),\;a(0)=a_0)
을 만족시키는 함수는 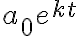 뿐임을 보여보자. 만약
뿐임을 보여보자. 만약 ) 가 위의 초기조건이 주어진 방정식의 해라면, // 음의 부호가 왜 나오지? 지금까지 다루던 두번째 방정식 말고 첫번째 붕괴 방정식?
가 위의 초기조건이 주어진 방정식의 해라면, // 음의 부호가 왜 나오지? 지금까지 다루던 두번째 방정식 말고 첫번째 붕괴 방정식?
 e^{-kt} \right) = a%27(t) e^{-kt} + a(t) \left( -k e^{-kt} \right) = 0)
이고, 따라서 e^{-kt}) 는 상수이다. 이 상수는
는 상수이다. 이 상수는 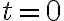 을 대입하면
을 대입하면 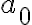 이므로,
이므로,
=a_0 e^{kt})
이다.
(김홍종 미적1+ p96)
13. 미분방정식 vs 대수방정식 ¶
이하 대충 상식으로 적었으므로 chk
... 미분방정식 대수방정식 비교
미분방정식 대수방정식 비교
| 대수방정식 | 미분방정식 | |
| 해,solution | 수,number | 함수,function |
| 해의 개수 | 1개 | 집합,set 형태라 무한히 많을 수 있음 - 앞에 곱해지는 상수,constant나 더해지는 적분상수,integration_constant가 무한히 많을 수 있어서 |
...
16. 관련주제, 추가예정, tbw ¶
AKA 미방, diff eq
Twins:
 미분방정식
미분방정식
 미분방정식
미분방정식
![[https]](/123/imgs/https.png) 수학백과: 미분방정식 (easy)
수학백과: 미분방정식 (easy)
![[https]](/123/imgs/https.png) 두산백과: 미분방정식
두산백과: 미분방정식
![[https]](/123/imgs/https.png) 경제학사전: 미분방정식
경제학사전: 미분방정식
https://everything2.com/title/Differential equation
https://planetmath.org/differentialequation
https://ncatlab.org/nlab/show/differential equation (very hard)
![[https]](/123/imgs/https.png) 수학백과: 미분방정식 (easy)
수학백과: 미분방정식 (easy)![[https]](/123/imgs/https.png) 두산백과: 미분방정식
두산백과: 미분방정식![[https]](/123/imgs/https.png) 경제학사전: 미분방정식
경제학사전: 미분방정식https://everything2.com/title/Differential equation
https://planetmath.org/differentialequation
https://ncatlab.org/nlab/show/differential equation (very hard)
https://en.citizendium.org/wiki/Differential_equation
https://proofwiki.org/wiki/Definition:Differential_Equation
https://calculus.subwiki.org/wiki/Differential_equation
https://proofwiki.org/wiki/Definition:Differential_Equation
https://calculus.subwiki.org/wiki/Differential_equation

