즉 평행사변형의 넓이와 관련이 있다.
1. Bazett ¶
일단 u, v에 모두 normal한 벡터는 두 방향이 있다. 그 중 right-hand rule을 따르는 방향으로의 단위법선벡터,unit_normal_vector
Geometric cross product:
)\vec{n})
여기서,
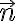 앞의 계수 : 평행사변형의 넓이
앞의 계수 : 평행사변형의 넓이
 : Unit normal vector obeying right-hand rule
: Unit normal vector obeying right-hand rule
Algebraic cross product:
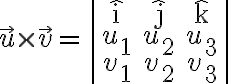
(용어(geometric/algebraic/determinant)를 알아두기 위해 적어놓음)
(https://youtu.be/xoeoGQ1Bzqc)
For 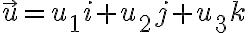 and
and 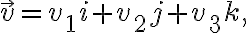
i+(u_1v_3-u_3v_1)j+(u_1v_2-u_2v_1)k)
Determinant cross product:(https://youtu.be/xoeoGQ1Bzqc)
3. 주요 성질 ¶
교환법칙,commutativity 비성립
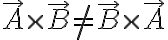
반교환법칙 anticommutativity? 성립 (anticommutative)

(since sin(-θ)=-sinθ)
결합법칙,associativity 비성립
\neq(\vec{A}\times\vec{B})\times\vec{C})
분배법칙,distributivity 성립
=\vec{A}\times\vec{B}+\vec{A}\times\vec{C})
\times\vec{c}=(\vec{a}\times\vec{c})+(\vec{b}\times\vec{c}))
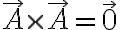
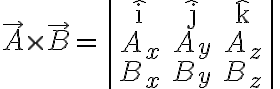
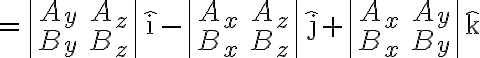
\cdot\vec{a}=0,)
\cdot\vec{b}=0)
(since sin(-θ)=-sinθ)
(since sin0=0)
//Stewart - Properties of the Cross Product(8e p819)에서 위에 아마 언급 안된 것 같은거
5. =(\vec{a}\times\vec{b})\cdot\vec{c})
//BAC-CAB 이미 있지만.. 여기 표현
6.=(\vec{a}\cdot\vec{c})\vec{b}-(\vec{a}\cdot\vec{b})\vec{c})
//BAC-CAB 이미 있지만.. 여기 표현
6.
증명은 \cdot\vec{a}) 를 계산하면 0이 나옴.
를 계산하면 0이 나옴. \cdot\vec{b}) 도 마찬가지. (내적이 0 ⇔ 직교)
도 마찬가지. (내적이 0 ⇔ 직교)
(Stewart)
8. 표준기저의 벡터곱 ¶
표준기저,standard_basis의 벡터곱
| i×i=0 | j×j=0 | k×k=0 | (0은 영벡터) |
| i×j=k | j×k=i | k×i=j | (cyclic order) // 순환순서,cyclic_order |
| j×i=−k | k×j=−i | i×k=−j | (anticyclic order?) (anticommutative) |
9. 행렬식(determinant)과의 관계 ¶
행렬식,determinant
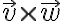 의
의
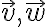 의 방향이
의 방향이
![[https]](/123/imgs/https.png) src)
src)
부호,sign는
그래서 두 - v에서 w로 회전하는 방향이 cw? (-)
- v에서 w로 회전하는 방향이 ccw? (+)
v의 열벡터를 왼쪽에, w의 열벡터를 오른쪽에 놓아 만든 행렬의 det와 같음.
(그리고 평행사변형의 면적과 관련)
(그리고 평행사변형의 면적과 관련)
more perpendicular => 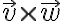 is bigger
is bigger
similar direction =>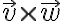 is smaller
is smaller
(similar direction =>
![[https]](/123/imgs/https.png) src)
src)10. TOASK ¶
TOASK: 텐서곱, outer product, kronecker product, tensor product 모두 같은거?
기호 ⊗ ?
기호 ⊗ ?

