AKA 선형공간, linear space
성질
따라서 '선형 벡터 공간' linear vector space 도 동의어? CHK
벡터공간에는 벡터,vector만 있다. 다른 것은 없다. (참고로 스칼라,scalar는 (스칼라 공간이 아니라?) 스칼라체 scalar_field에 있다. - curr 체,field2023-09-13... 
scalar_field이건 영어로 스칼라장,scalar_field과 구분이 안 되나? / + 다른 표현은 없는지?
Ans:
한국어:
스칼라체를 거쳐 ![[https]](/123/imgs/https.png)
수학백과 벡터공간 페이지에서 스칼라체 검색하면 상수체 라고도 한다고. 
스칼라체 
스칼라체 상수체 상수체
영어:field_of_scalars임. 
field_of_scalars은 redirected. 스칼라장을 설명하는 Scalar_field은 맨 위에 disambiguation으로 처리. )
F가 체,field일 때, Fn의 부분집합 V가 다음 조건을 만족하면, V를 F위의 벡터공간이라 함.scalar_field이건 영어로 스칼라장,scalar_field과 구분이 안 되나? / + 다른 표현은 없는지?Ans:
한국어:
스칼라체를 거쳐 수학백과 벡터공간 페이지에서 스칼라체 검색하면 상수체 라고도 한다고. 스칼라체 스칼라체 상수체 상수체영어:
field_of_scalars임. field_of_scalars은 redirected. 스칼라장을 설명하는 Scalar_field은 맨 위에 disambiguation으로 처리. )성질
- 항상 덧셈에 대해 닫혀 있음
- 덧셈의 항등원 0을 원소로 가짐 (항등원,identity_element) // additive_identity { pagename tbd. 참고, kms additive : https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=additive .... Additive_identity ...
additive_identity }
- 덧셈의 역원 존재 (덧셈,addition의 역원,inverse_element) // additive_inverse { Additive_inverse ... additive_identity }
- 수학에서 보통 써오던 집합,set은 대부분 벡터공간이라고 하네. (ex.
연속함수의 집합, 미분가능한 함수들의 집합 등)
- n차원 좌표공간 Fn
- ℝ3
: column vector with 3 components
- ℝ3
- 평면,plane
= set of all polynomials
= set of all polynomials of degree
= set of all m×n matrices
= set of all continuous functions on
= set of all continuous functions on
Contents
3. tmp 영공간과 열공간 ¶
Ax=0의 해들이 이루는 벡터공간은 영공간,null_space
Ax=b의 해들이 이루는 벡터공간은 열공간,column_space
이 둘은 homogeneous/inhomogeneous와 관련되었다고.
Ax=b의 해들이 이루는 벡터공간은 열공간,column_space
이 둘은 homogeneous/inhomogeneous와 관련되었다고.
Thm. 해,solution가 존재하는 연립일차방정식,system_of_linear_equations Ax=b의 해집합,solution_set을 S,
대응되는 연립일차방정식 Ax=0의 해집합을 SH라 표기. (H는 homogeneous인듯)
Ax=b의 임의의 해를 s라 하면 다음 식이 성립.
// s+SH 는 {s}∪SH를 뜻하나???
대응되는 연립일차방정식 Ax=0의 해집합을 SH라 표기. (H는 homogeneous인듯)
Ax=b의 임의의 해를 s라 하면 다음 식이 성립.
S=s+SH={s+h|h∈SH}
// 즉 s∈S// s+SH 는 {s}∪SH를 뜻하나???
뜻: 우변이 0이 아닌 inhomogeneous방정식의 일반해는, 한 해만 선택한 다음 우변이 0인 homogeneous방정식의 해집합에 더하기만 하면 만들 수 있다.
pf. 연립방정식 Ax=b의 임의의 해를 s라 하자.
그 외의 또 다른 어떤 해를 t라 하면, t∈S이고
그러면 t=s+h∈{s}+SH라 할 수 있고, t∈S이므로
역으로, t∈{s}+SH라 가정한다. 그러면 어떤 h∈SH에 대해 t=s+h라 할 수 있다. 이 때
그 외의 또 다른 어떤 해를 t라 하면, t∈S이고
Ax=b
At=b
A(t-s)=b-b=0
이므로 t-s∈SH이다. 여기서 t-s=h라 하면, h는 연립방정식 Ax=0의 해이므로 h∈SH이다.At=b
A(t-s)=b-b=0
그러면 t=s+h∈{s}+SH라 할 수 있고, t∈S이므로
S⊆{s}+SH ......(1)
가 성립.역으로, t∈{s}+SH라 가정한다. 그러면 어떤 h∈SH에 대해 t=s+h라 할 수 있다. 이 때
At=A(s+h)=As+Ah=b+0=b
이므로 t는 연립방정식 Ax=b의 해가 되어 t∈S이고 S는 가정 상 {s}+SH보다 큰 집합이므로{s}+SH⊆S ......(2)
이다. 따라서 (1), (2)에 대해 S={s}+SH가 성립한다.4. TMP 벡터공간임을 인정받으려면 반드시 따라야 할 규칙 CHK ¶
(벡터공간 내 임의의 벡터 v,w를 가정. 임의의 상수 c,d를 가정.)
1. 더한 결과 v+w는 같은 벡터 공간에 존재.
2. 상수곱의 결과 cv는 같은 벡터 공간에 존재.
3. 모든 경우의 cv+dw 조합(선형결합,linear_combination) 결과가 같은 벡터 공간에 존재.
1. 더한 결과 v+w는 같은 벡터 공간에 존재.
2. 상수곱의 결과 cv는 같은 벡터 공간에 존재.
3. 모든 경우의 cv+dw 조합(선형결합,linear_combination) 결과가 같은 벡터 공간에 존재.
5.1. 정의 ¶
체 F도 집합이고, 벡터공간 V도 집합,set이다.
Def. Vector space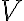 
over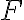 
아무튼 V는 벡터들의 집합, F는 스칼라들의 집합.
= a set of vectors with two operations (+,·)
여기서아무튼 V는 벡터들의 집합, F는 스칼라들의 집합.
그래서 다음 조건을 만족해야 한다.
- 닫힘 closed
- x+y=y+x
- (x+y)+z=x+(y+z)
- ∃0∈V such that x+0=x .... 0∈V .... 수 영,zero 아니고 벡터인 영벡터,zero_vector
- ∀x∈V such that 1·x=x .... 1∈F .... 수 하나,one 맞음 (스칼라)
- (a·b)·x = a·(b·x) .... 여기서 첫번째 ·는 scalar와 scalar의 곱셈이고, 두번째 ·는 scalar와 vector의 곱셈. (QQQ scalar_multiple ?)
- a(x+y)=ax+ay
- (a+b)x=ax+bx
5.2. 벡터공간의 예 .... 이하 CLEANUP ¶
// 그래서 F를 실수로 생각하면
ex2.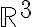
over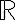 
ex2.
// 복소수 4-tuple로 생각하면
ex3.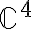
over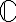 
ex3.
ex4. 행렬도 vector space가 될 수 있음. 조건만 만족하면..
m by n "$(m\times n)$")
행렬
![$M_{m\times n}(F)=\left\lbrace [a_{i,j}]_{m\times n} \middle| a_{i,j}\in F \right\rbrace$](/123/cgi-bin/mimetex.cgi?\Large M_{m\times n}(F)=\left\lbrace [a_{i,j}]_{m\times n} \middle| a_{i,j}\in F \right\rbrace "$M_{m\times n}(F)=\left\lbrace [a_{i,j}]_{m\times n} \middle| a_{i,j}\in F \right\rbrace$")
 "$\begin{bmatrix}2&3&4\\5&6&7\end{bmatrix}\in M_{2\times 3}(F)$")
Zero in=\begin{bmatrix}0&0&0\\0&0&0\end{bmatrix} "$M_{2\times 3}(F)=\begin{bmatrix}0&0&0\\0&0&0\end{bmatrix}$")
m by n
Zero in
ex5. A set of functions from ![$[0,1]$](/123/cgi-bin/mimetex.cgi?\Large [0,1] "$[0,1]$")
to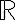
이 vector space의 zero_vector에 해당하는 것은 영함수,zero_function.
어떤 vector의(ie 함수의) additive_inverse는 x축 대칭인 함수.
이 vector space의 zero_vector에 해당하는 것은 영함수,zero_function.
어떤 vector의(ie 함수의) additive_inverse는 x축 대칭인 함수.
ex6. 유한차수다항식들의 집합  "$V=P(\mathbb{R})$")
// 이건 P over R이며, P는 polynomial, R은 계수가 실수에서 왔다는 뜻
=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_0\in V "$f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_0\in V$")
=b_nx^n+b_{n-1}x^{n-1}+\cdots+b_0\in V "$g(x)=b_nx^n+b_{n-1}x^{n-1}+\cdots+b_0\in V$")
이건 다음과 같은 성질들을 만족하므로 vector space임.
+g(x)\in V "$f(x)+g(x)\in V$")
\in V "$cf(x)\in V$")
Zero of V=0
Inverse of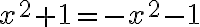
Inverse of
ex7. (벡터공간 아님)
 \middle| a_1,a_2\in\mathbb{R} \right\} "$S=\left\{ (a_1,a_2) \middle| a_1,a_2\in\mathbb{R} \right\}$")
// 즉 2차원 평면 위의 한 점으로 생각
+(b_1,b_2)=(a_1+b_1,a_2-b_2) "$(a_1,a_2)+(b_1,b_2)=(a_1+b_1,a_2-b_2)$")
=(ca_1,ca_2) "$c(a_1,a_2)=(ca_1,ca_2)$")
이렇게 정의한 
는 벡터공간인가?
commutative, associative 조건 때문에 아니다
일단 연산에 뺄셈이 있어서 vector addition에 대한 교환법칙이 성립 X
commutative, associative 조건 때문에 아니다
일단 연산에 뺄셈이 있어서 vector addition에 대한 교환법칙이 성립 X
ex8. (벡터공간 아님) // 이것도 2차원 평면
\middle| a_1,a_2\in\mathbb{R}\right\rbrace "$S=\left\lbrace (a_1,a_2)\middle| a_1,a_2\in\mathbb{R}\right\rbrace$")
+(b_1,b_2)=(a_1+b_1,0) "$(a_1,a_2)+(b_1,b_2)=(a_1+b_1,0)$")
=(ca_1,0) "$c(a_1,a_2)=(ca_1,0)$")
이렇게 정의한 는 벡터공간인가?
Sol.
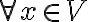s.t. 1·x=x 이어야 하는데, 즉 1을 곱하면 자기자신이어야 하는데, 자기자신이 될 수가 없다.
예를 들어 1·(3,5)=(3,0) 이 되는데 이게 (3,5)가 아니다.
s.t. x+0=x 이어야 하는데, 즉 0을 더하면 자기자신이어야 하는데, 더하기만 하면 항상 뒤를 0으로 만들어 버린다.
이렇게 정의한
Sol.
예를 들어 1·(3,5)=(3,0) 이 되는데 이게 (3,5)가 아니다.
5.3.1. Thm 1.1 cancellation_law ¶
∀x,y,z∈V,
x+z=y+z ⇒ x=z // 즉 cancellation을 할 수 있는지에 대한 정리. easy.
x+z=y+z ⇒ x=z // 즉 cancellation을 할 수 있는지에 대한 정리. easy.
Pf.
공리에 따라 덧셈의 역원이 존재하므로 ∃(-z). 양변에 더하면
공리에 따라 덧셈의 역원이 존재하므로 ∃(-z). 양변에 더하면
(x+z)+(-z)=(y+z)+(-z)
덧셈 결합법칙x+(z+(-z))=y+(z+(-z))
덧셈의 역원을 더하면 영벡터가 되므로x+0=y+0
x=y
결론: vector space에선 덧셈,addition에 대해서 cancellation을 할 수 있다.x=y
5.3.1.1. Cor 1 identity 0 is unique - 덧셈 항등원 0의 유일성 ¶
uniqueness 증명은 방법이 하나밖에 없다 - 두 개 있다고 가정하고, 그 둘이 같을 수 밖에 없음을 증명하는 것
pf. zero vector가 0과 0' 두개라고 가정한다. Suppose we have two zeroes 0 and 0'
pf. zero vector가 0과 0' 두개라고 가정한다. Suppose we have two zeroes 0 and 0'
x+0=x=x+0'
x+0=x+0'
By cancellation,x+0=x+0'
0=0'
결론: 영벡터,zero_vector의 유일성,uniqueness: 영벡터는 벡터공간 안에 여러 개 있을 수가 없고 하나만 존재한다.5.3.1.2. Cor 2 inverse is unique - 덧셈의 역원의 유일성 ¶
Pf. x의 덧셈에 대한 역원이 하나가 아니고 두 개 a, b가 있다고 가정. Suppose we have two inverses of x which are a and b.
x+a=0
x+b=0
위 Cor 1에서 0은 유일하다고 했으므로x+b=0
x+a=x+b
By cancellation,a=b
5.3.2. Thm 1.2 ¶
벡터에 스칼라 0을 곱하면 영벡터가 된다.
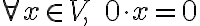(주의: 앞의 0은 scalar zero, 뒤의 0은 zero vector... 이하 0과 \vec{0} 을 일부러 구분 표기하지 않았음 - 내가 틀릴수 있으므로)
pf.
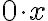// 0=0+0이라는 일종의 technique?? 을 쓴다...
\cdot x "$=(0+0)\cdot x$")
// 여기 분배법칙 쓰면
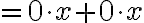
By cancellation,
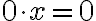
영벡터에 어떤 스칼라를 곱해도 영벡터이다.
pf.
 "$=a\cdot(0+0)$")
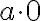
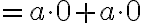
By cancellation,
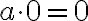
∀x∈V, ∀a∈F // x는 벡터고 a는 스칼라이다.
뒷쪽등호
(−a)·x = −(a·x) = a·(−x)
pf. 앞쪽등호a·x+(−a)·x
= (a+(−a))·x
= 0·x
= 0
∴ (−a)·x is the inverse of a·x= (a+(−a))·x
= 0·x
= 0
뒷쪽등호
a·x + a·(−x)
= a·(x+(−x))
= a·0
= 0
∴ a·(−x) is the inverse of a·x= a·(x+(−x))
= a·0
= 0
6. 정의; tmp CHK ¶
{
일단 잘 안 쓰이는 용어 잠시 찾아보니 '가법'은 다음을 얘기하는 듯. 단순 덧셈,addition 말고도. CHK. from![[http]](/123/imgs/http.png)
선형대수 George Nakos 벡터공간 소개부분 요약
{
찾다 보니 가법성(additivity)이란 게 있는데=f(a)+f(b) "$f(a+b)=f(a)+f(b)$")
라는 뜻이라고. src
일단 잘 안 쓰이는 용어 잠시 찾아보니 '가법'은 다음을 얘기하는 듯. 단순 덧셈,addition 말고도. CHK. from
선형대수 George Nakos 벡터공간 소개부분 요약{
- 모든
에 대하여
이다.
- 모든
이다.
- 모든
에 대하여
이다.
- V의 영이라고 부르는 일의적인 원소
가 존재하여, 모든
에 대하여
를 만족한다.
- 각
가 존재하여
을 만족한다.
- 덧셈에 닫혀있음
- 덧셈 교환법칙 성립
- 덧셈 결합법칙 성립
- 덧셈의 항등원 0 존재
- 덧셈의 역원 존재
찾다 보니 가법성(additivity)이란 게 있는데
src2021-05-21 additivity에 대한 설명
도형 D가 두 부분으로 나뉘어져서 D = D1 ∪ D2라고 쓸 수 있고 이 두 부분은 교차하는 부분이 없어서 D1 ∩ D2 = ∅일 때, 넓이 A는 다음 성질을 만족시킨다:
=A(D_1)+A(D_2) "$A(D)=A(D_1)+A(D_2)$")
이것을 넓이 함수의 additivity라고 한다.
from AnamLectureNotesVol1_20200210.pdf
}
도형 D가 두 부분으로 나뉘어져서 D = D1 ∪ D2라고 쓸 수 있고 이 두 부분은 교차하는 부분이 없어서 D1 ∩ D2 = ∅일 때, 넓이 A는 다음 성질을 만족시킨다:
from AnamLectureNotesVol1_20200210.pdf
}
어떤 집합 V에 대해,
- 가법
- 스칼라곱 (scalar product(이거)가 아니라 스칼라를 곱하는 것을 뜻하는지 CHK. 관련pages: 곱셈,multiplication and 곱,product)
벡터공간은 아래 세 성질을 만족하는 공간.
- 가법에 대해 가환군이 된다. (가환군 = commutative group = 아벨군 = abelian group, curr see 군,group)
- 스칼라곱에 대해 결합법칙이 성립한다. (결합법칙,associativity)
- 가법과 스칼라 곱을 함께 쓸 때 분배법칙이 성립한다. (분배법칙,distributivity)
(참고) 가법에 대한 가환군,commutative_group의 예로는 Z, Q, R, C가 있다 (자연수는 0과 음수가 없어서, 가법에 대해 군이 아님)
스칼라(여기서 스칼라는 체,field를 말함)에 대해 벡터공간을 분류 가능.
https://m.blog.naver.com/sglee84/110045627887 (선형대수-2)
https://beckho.tistory.com/17 (벡터공간)
}
실수체를 쓰는 실벡터공간 real vector space real_vector_space https://mathworld.wolfram.com/RealVectorSpace.html
복소수체를 쓰는 복소벡터공간 complex vector space_complex_vector space https://mathworld.wolfram.com/ComplexVectorSpace.html
이상 참고:복소수체를 쓰는 복소벡터공간 complex vector space_complex_vector space https://mathworld.wolfram.com/ComplexVectorSpace.html
https://m.blog.naver.com/sglee84/110045627887 (선형대수-2)
https://beckho.tistory.com/17 (벡터공간)
}
8. Definition from Lay 4.1 ¶
A vector space is a nonempty set 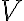of objects, called vectors, on which are defined two operations, called addition and multiplication by scalars, subject to the ten axioms listed below. The axioms must hold for all vectors 
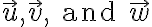in 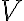and for all scalars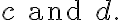 
(sum의 존재)
such that
- For each
such that
(scalar multiple의 존재)
12. 벡터공간의 차원 ¶
벡터공간의 기저가 유한 개의 벡터를 포함하면 그 벡터공간은 유한차원(finite dimensional), 그렇지 않으면 무한차원(infinite dimensional)이라 한다. 구간 
위에서 
번 연속적으로 미분가능한 함수로 된 함수공간,function_space  "$C^n(I)$")
는 무한차원벡터공간의 한 예이다.
(Zill 6e ko 정의 7.6.5 p443)
Q: 벡터장,vector_field과 차이?
Twins:
수학백과: 벡터공간
수학의 세계: 벡터공간 - snu 교양과목 교재에서 짧게 언급한 부분
https://mathworld.wolfram.com/VectorSpace.html (8개의 조건)
https://planetmath.org/vectorspace
https://everything2.com/title/vector space
https://en.citizendium.org/wiki/Vector_space
https://artofproblemsolving.com/wiki/index.php/Vector_space
수학백과: 벡터공간수학의 세계: 벡터공간 - snu 교양과목 교재에서 짧게 언급한 부분https://mathworld.wolfram.com/VectorSpace.html (8개의 조건)
https://planetmath.org/vectorspace
https://everything2.com/title/vector space
https://en.citizendium.org/wiki/Vector_space
Up:
벡터,vector
공간,space
선형대수,linear_algebra
선형성,linearity
대수적 대상 algebraic_object - 대수학,algebra 대상,object
Ref:공간,space
선형대수,linear_algebra
선형성,linearity
대수적 대상 algebraic_object - 대수학,algebra 대상,object
벡터공간의 기본개념 http://matrix.skku.ac.kr/sglee/linear/ocu/20501.html
예 몇가지: 항공대 최도훈 강의http://kocw.net/home/search/kemView.do?kemId=1285101
http://matrix.skku.ac.kr/sglee/linear/ocu/20501.html예 몇가지: 항공대 최도훈 강의
http://kocw.net/home/search/kemView.do?kemId=1285101