Sub:
기울기,gradient ∇(scalar_field)=(vector_field)
발산,divergence ∇·(vector_field)=(scalar_field)
회전,curl ∇×(vector_field)=(vector_field)
라플라시안,Laplacian (AKA 라플라스_연산자,Laplace_operator) ∇·∇(scalar_field)=(scalar_field)? CHK
선속,flux
델,del,나블라,nabla ∇
선적분,line_integral은 벡터장내 벡터의 적분인가?
관련:발산,divergence ∇·(vector_field)=(scalar_field)
회전,curl ∇×(vector_field)=(vector_field)
라플라시안,Laplacian (AKA 라플라스_연산자,Laplace_operator) ∇·∇(scalar_field)=(scalar_field)? CHK
선속,flux
델,del,나블라,nabla ∇
선적분,line_integral은 벡터장내 벡터의 적분인가?
Contents
- 1. 벡터함수의 도함수
- 2. 정리
- 3. cleanup
- 4. ex. (+물리적 해석)
- 5. 물리에 응용: 운동량,momentum, 각운동량,angular_momentum 관련 TOCLEANUP
- 6. from 이정일 강의; TOCLEANUP TOMERGE
- 7. 벡터연산자 grad/div/curl
- 8. nabla, del, ∇ 기호의 정의
- 9. grad, gradient, 기울기, 경사
- 10. div, divergence, 발산
- 11. curl, rot, rotation, 회전
- 12. 라플라시안 Laplacian
- 13. 비교 표
- 14. curl(grad(f))=0
- 15. div(curl(F))=0
- 16. grad/div/curl: O'Neil 표현
- 17. div, grad, curl, and all that
- 18. Textbooks
- 19. Further Ref / Twins
2. 정리 ¶
(f는 scalar function)
스토크스_정리,Stokes_theorem
그린_정리,Green_theorem
3. cleanup ¶
정의
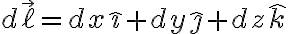
위 뜻을 이제는 좀 정확히 알 듯.
일단 먼저
=\frac{dx}{dt} \;\to\; dx=x%27(t)dt)
=\frac{dy}{dt} \;\to\; dy=y%27(t)dt)
시작: 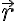 이
이
=x(t)\hat{i}+y(t)\hat{j})
이면 이것을 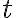 로 미분하면
로 미분하면
=x%27(t)\hat{i}+y%27(t)j) ...... 이하 i,j 위에 hat 생략
...... 이하 i,j 위에 hat 생략
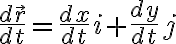
양변에 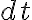 를 곱하면 (이하 셋은 순서 단계가 아니라 모두 같은 것)
를 곱하면 (이하 셋은 순서 단계가 아니라 모두 같은 것)
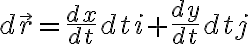
dti+y%27(t)dtj)
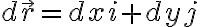
관련: 벡터미적분, 미분,differential
좌표계,coordinate_system#s-11(벡터미적분을 위한 좌표계의 디퍼렌셜, 미소xx)
벡터함수,vector_function
에 관련내용 있음.
여러 좌표계의 미소길이/미소면적/미소부피 내용 있음
위치벡터,position_vector벡터함수,vector_function
에 관련내용 있음.
at 2020-10-08 src: ![[https]](/123/imgs/https.png) Khan Multivar. Calculus differential of a vector valued function
Khan Multivar. Calculus differential of a vector valued function
KWs: derivative/differential of vector valued function / position vector function
![[https]](/123/imgs/https.png) Khan Multivar. Calculus differential of a vector valued function
Khan Multivar. Calculus differential of a vector valued functionKWs: derivative/differential of vector valued function / position vector function
4. ex. (+물리적 해석) ¶
자기자신을 내적해도 상수이므로

이것은 원,circle 궤도,orbit - 접선,tangent_line이 원 위의 점에 대한 위치벡터,position_vector와 직각(직교성,orthogonality)인.
5. 물리에 응용: 운동량,momentum, 각운동량,angular_momentum 관련 TOCLEANUP ¶
운동량(p)의 시간 미분은 힘(F)이다.
=\frac{\mathrm{d}m}{\mathrm{d}t}\cdot\vec{v}+m\cdot\frac{\mathrm{d}\vec{v}}{\mathrm{d}t})
질량은 시간에 대해 변하지 않으므로, (dm/dt=0)

마찬가지 방법으로, 각운동량(L)의 시간 미분은 토크,torque(τ)이다.
=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\times\vec{p}+\vec{r}\times\frac{\rm d\vec{p}}{\mathrm{d}t})
dr/dt=0이 된다고 한다 why?
그리고 dp/dt가 위에서 F였으므로,
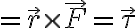
CHK
그리고 dp/dt가 위에서 F였으므로,
7. 벡터연산자 grad/div/curl ¶
| 연산대상 | 연산결과 | |
| grad | 스칼라장 | 벡터장 |
| div | 벡터장 | 스칼라장 |
| curl | 벡터장 | 벡터장 |
Q: 그럼 스칼라장을 스칼라장으로 만드는 것은? 단순 수치를 더하거나 곱함? or 라플라시안?
| 직각좌표계 | |||
| 원통좌표계 | |||
| 구면좌표계 |
dr에 뭔가 곱해지는 것이 있으면 ∇에는 같은 것을 나누는 것이 있음
grad, div, curl을 직각좌표계로 대표하기(? 표현하기?)
ALSOIN 좌표계, 델,del,나블라,nabla
CHK; from https://www.youtube.com/watch?v=Sa7xDuWEvZ4 스토크스 정리와 다이버젠스 정리 2분 (차동우)
| grad | |
| div | |
| curl |
ALSOIN 좌표계, 델,del,나블라,nabla
CHK; from https://www.youtube.com/watch?v=Sa7xDuWEvZ4 스토크스 정리와 다이버젠스 정리 2분 (차동우)
14. curl(grad(f))=0 ¶
divergence와 curl의 성질
the curl of its gradient is the zero vector
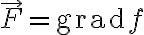 를 뜻하므로.
를 뜻하므로.
curl(grad(f))=0̅
=\vec{0})
the curl of any conservative vector field is zero (vector?)curl(F)=0̅
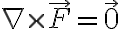
왜냐? conservative라는 것 자체가 위에서 15. div(curl(F))=0 ¶
(아마 여기도 조건이 ..  가 연속된 2계편미분을 가지면,)
가 연속된 2계편미분을 가지면,)
the divergence of a curl is zero
증명: (위와 마찬가지) 연속이면 미분 순서가 중요하지 않아서 다 cancel되어 (Clairaut's thm) 값이 0이 됨.
17. div, grad, curl, and all that ¶
Divergence Theorem
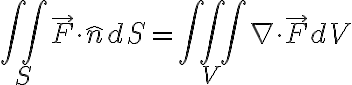
Stokes' Theorem
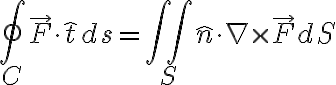
Identities Involving the Operator ∇* (이하 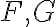 에 벡터 표시
에 벡터 표시 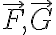 생략)
생략)
=f\nabla g + g\nabla f)
=(G\cdot\nabla)F+(F\cdot\nabla)G+F\times(\nabla\times G)+G\times(\nabla\times F))
=f\nabla\cdot+F\cdot\nabla f) (????)
(????)
=G\cdot(\nabla\times F)-F\cdot(\nabla\times G))
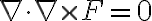
=f\nabla\times F+(\nabla f)\times F)
=(G\cdot \nabla)F-(F\cdot \nabla)G+F(\nabla\cdot G)-G(\nabla\cdot F))
=\nabla(\nabla\cdot F)-\nabla^2 F)
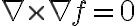
 는 위치의 스칼라 함수이고
는 위치의 스칼라 함수이고 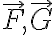 는 위치의 벡터 함수.
는 위치의 벡터 함수.
(div, grad, curl, and all that 4e 책의 맨 앞)
19. Further Ref / Twins ¶
![[https]](/123/imgs/https.png) 수학백과: 벡터해석
수학백과: 벡터해석https://encyclopediaofmath.org/wiki/Vector_calculus
"An obsolete name … 벡터대수학 vector_algebra{ https://encyclopediaofmath.org/wiki/Vector_algebra }, 벡터해석학
vector_algebra{ https://encyclopediaofmath.org/wiki/Vector_algebra }, 벡터해석학 vector_analysis{ https://encyclopediaofmath.org/wiki/Vector_analysis }로 구성... "
vector_analysis{ https://encyclopediaofmath.org/wiki/Vector_analysis }로 구성... "
grad, div, curl, laplacian은 연산자,operator? 미분연산자? 델 연산자가 포함된 곱셈 규칙 product rule with del operator
https://freshrimpsushi.github.io/posts/product-rule-with-del-operator/
https://freshrimpsushi.github.io/posts/product-rule-with-del-operator/
https://ghebook.blogspot.com/2010/07/vector.html
https://ghebook.blogspot.com/2010/08/vector-identity.html
and
https://ghebook.blogspot.com/2020/07/vector-calculus.html
https://ghebook.blogspot.com/2010/08/vector-identity.html
and
https://ghebook.blogspot.com/2020/07/vector-calculus.html
Video
Dr. Bazett, Calculus IV: Vector Calculus
https://www.youtube.com/playlist?list=PLHXZ9OQGMqxfW0GMqeUE1bLKaYor6kbHa
Dr. Bazett, Calculus IV: Vector Calculus
https://www.youtube.com/playlist?list=PLHXZ9OQGMqxfW0GMqeUE1bLKaYor6kbHa

