정의역 실수는 시간 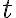 인 경우가 많음. 아니어도 상관없음. mklink: { 매개변수,parameter 매개변수방정식,parametric_equation 매개곡선,parametric_curve }
인 경우가 많음. 아니어도 상관없음. mklink: { 매개변수,parameter 매개변수방정식,parametric_equation 매개곡선,parametric_curve }
QQQ vector-valued function과 완전히 같은건가? 관계?
1. 설명 ¶
매개변수방정식 ,\; y=g(t),\; z=h(t)) 로 나타낼 수도 있다.
로 나타낼 수도 있다.
모든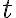 에 대해 벡터
에 대해 벡터 ,\ g(t),\ h(t))) 의 시점을 원점으로 놓으면 종점은
의 시점을 원점으로 놓으면 종점은 ,\ g(t),\ h(t))) 이다. 세 함수
이다. 세 함수 , g(t), h(t)) 가 연속이면 벡터
가 연속이면 벡터 ) 의 종점은 위 매개방정식이 나타내는 곡선을 나타낸다.
의 종점은 위 매개방정식이 나타내는 곡선을 나타낸다.
모든
2020-09-12
벡터함수
=x(t)\vec{i}+y(t)\vec{j}+z(t)\vec{k})
여기서 ) 는 3D 공간에서 curve의 위치벡터,position_vector로 볼 수 있고, 각 t에 대해 origin에서 점
는 3D 공간에서 curve의 위치벡터,position_vector로 볼 수 있고, 각 t에 대해 origin에서 점 ,y(t),z(t))) 까지 그은 화살표로 생각할 수 있다. 이러면 좌표함수들(coordinate functions)은 curve의 매개변수방정식,parametric_equation이다. F의 미분은
까지 그은 화살표로 생각할 수 있다. 이러면 좌표함수들(coordinate functions)은 curve의 매개변수방정식,parametric_equation이다. F의 미분은
=x%27(t)\vec{\imath}+y%27(t)\vec{\jmath}+z%27(t)\vec{k})
(생각: 기저,basis(i, j, k)를 상수로 생각하고 나머지 함수들은 미분한 그런 모양새....)
벡터함수
5. 2017-12-25, 최성우, kocw ¶
벡터함수의 연속
=\vec{r}(a)) 일 때,
일 때, 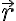 은
은  에서 연속
에서 연속
예: =(\cos t,\; \sin t,\; t)=\cos(t)\hat{\rm i}+\sin(t)\hat{\rm j}+t\hat{\rm k}) 는 나선(helix, spiral)가 됨
는 나선(helix, spiral)가 됨
=\frac{d}{dt}\vec{r}=\frac{d\vec{r}}{dt}:=\lim_{h\to 0}\frac{\vec{r}(t+h)-\vec{r}(t)}{h})
이것을 xy평면에 비춘 모양은 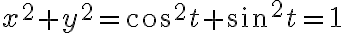 이므로 원이 됨
이므로 원이 됨
벡터미분의 정의벡터함수에서도 미적분학의기본정리,FTC가 성립
6. Thomas Ch11 벡터함수 ¶
원점,origin에서부터, 시간 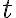 일 때 입자의 위치,position
일 때 입자의 위치,position ,g(t),h(t))) 까지로 정의된 벡터,vector
까지로 정의된 벡터,vector
=\overrightarrow{OP}=f(t)\hat{i}+g(t)\hat{j}+h(t)\hat{k})
는 입자의 위치벡터,position_vector이다.
함수,function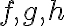 는 위치벡터의 성분 또는 성분함수(component function)이다.
는 위치벡터의 성분 또는 성분함수(component function)이다.
함수,function
정의역  위에서의 벡터함수(vector function) 또는 벡터값함수(vector-valued function)란,
위에서의 벡터함수(vector function) 또는 벡터값함수(vector-valued function)란,  의 각 원소를 공간,space의 한 벡터로 대응시키는 규칙이다.
의 각 원소를 공간,space의 한 벡터로 대응시키는 규칙이다.
 는 실수,real_number일수도, 평면,plane일수도, 공간일수도 있다. 평면이나 공간에서 정의된 벡터함수는 벡터장,vector_field을 나타내게 된다.
는 실수,real_number일수도, 평면,plane일수도, 공간일수도 있다. 평면이나 공간에서 정의된 벡터함수는 벡터장,vector_field을 나타내게 된다.
실수값함수를 벡터함수와 구별하기 위해 스칼라함수(scalar function)라고 부른다.
6.1. 벡터값함수의 극한 ¶
정의역  에서 정의된 한 벡터함수
에서 정의된 한 벡터함수
=f(t)\hat{i}+g(t)\hat{j}+h(t)\hat{k})
과 한 벡터 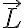 이 있다.
이 있다.
임의의 양수 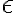 에 대해서,
에 대해서,
적당한 양수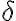 가 존재하여,
가 존재하여,
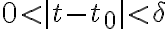 인 모든
인 모든 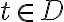 에 대해,
에 대해,
-\vec{L}|<\epsilon) 을 만족할 때,
을 만족할 때,
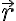 은
은 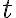 가
가 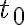 로 접근할 때 극한
로 접근할 때 극한 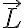 을 갖는다고 하고
을 갖는다고 하고
=\vec{L})
로 쓴다.
적당한 양수
Up: 극한,limit
7. 공간곡선 space curve ¶
// from 김도형 http://www.kocw.net/home/search/kemView.do?kemId=1141060 6 1:23m
{
벡터함수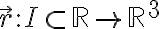
,g(t),h(t) \right\rangle)
를 매개변수방정식,parametric_equation으로 생각하면
,g(t),h(t) \right\rangle \middle| t\in I \right\}) 을 공간곡선으로 생각할 수 있다.
을 공간곡선으로 생각할 수 있다.
{
벡터함수
를 매개변수방정식,parametric_equation으로 생각하면


![[http]](/123/imgs/http.png)