qqq 시간과 공간을 포괄하는 단어는 자원resource인가? computational_resource? (chkout: 
Computational_resource)
qqq 현재 여기서 말하는 것은 모두 계산복잡도,computational_complexity - 계산 복잡도 이론(computational complexity theory)? 그렇다면 여기 속하지 않는 다른 복잡도가 있으면, 무엇이? 그리고 그게 서술되면 fork..
computational complexity vs algorithmic complexity보면 별 차이 없는 듯.
Computational_resource)qqq 현재 여기서 말하는 것은 모두 계산복잡도,computational_complexity - 계산 복잡도 이론(computational complexity theory)? 그렇다면 여기 속하지 않는 다른 복잡도가 있으면, 무엇이? 그리고 그게 서술되면 fork..
저 둘이 가장 많이 언급되고 중요한 것은 확실, 그리고 둘은 trade-off 관계. AST의 자료구조,data_structure 구현,implementation에서도 그렇고 알고리듬,algorithm에서도 그렇고 ....
computational과 algorithmic_complexity 관계는? ... computational complexity vs algorithmic complexity보면 별 차이 없는 듯.계산,computation, 계산가능성,computability, 알고리듬,algorithm 복잡도_분석,complexity_analysis (= algorithmic complexity?) 에서
시간복잡도,time_complexity - 알고리즘 수행 시간 분석
{
시간복잡도,time_complexity - 알고리즘 수행 시간 분석
{
| 최악의 경우 | worst case | 수행시간이 가장 오래 걸리는 경우 |
| 최선의 경우 | best case | 수행시간이 가장 적게 걸리는 경우 |
| 평균적인 경우 | average case |
가장 좋은 경우는 constant time
보통 polynomial time이 걸리면 reasonable
까다로움? 다루기어려움? intractability .... intractability 
intractability
intractable한 문제: polynomial time에 풀 수 있는 문제
tractable한 문제: polynomial time에 풀 수 있는 문제
intractable한 문제: polynomial time에 풀 수 없는 문제
intractability는 알고리듬,algorithm의 성질이 아니라 문제,problem의 성질임.[1]
선형시간 linear time - ex. 선형검색 linear_search
로그시간 logarithmic time - ex. 이진검색 binary_search
지수시간 exponential time
intractabilitytractable한 문제: polynomial time에 풀 수 있는 문제
intractable한 문제: polynomial time에 풀 수 없는 문제
intractability는 알고리듬,algorithm의 성질이 아니라 문제,problem의 성질임.[1]
think: 한 문제를 해결하는 algorithm은 한 가지가 아니라 여러가지임을 상기...
관련된 표현(misc, del ok):(program or application의) speed, running time, performance,
더 작은 시간복잡도의 algorithm으로 바꾸는 것은 program 최적화,optimization의 일종
상수시간 constant time더 작은 시간복잡도의 algorithm으로 바꾸는 것은 program 최적화,optimization의 일종
선형시간 linear time - ex. 선형검색 linear_search
로그시간 logarithmic time - ex. 이진검색 binary_search
지수시간 exponential time
Up: 시간,time 복잡도,complexity
}
공간복잡도,space_complexity - 알고리즘,algorithm이 쓰는 기억 공간메모리,memory. +storage? 분석
보통 문제(입력?) 크기
에 대한 함수,function으로 나타냄
}
공간복잡도,space_complexity - 알고리즘,algorithm이 쓰는 기억 공간메모리,memory. +storage? 분석
보통 문제(입력?) 크기
algorithmic complexity
computational complexity (=time complexity?)
computational complexity (=time complexity?)
Contents
- 1. Big O notation
- 2. Big Ω notation
- 3. Big Θ notation
- 4. Little o Notation
- 5. Little ω Notation
- 6. 이상
- 7. P, NP 대략적 설명
- 8. P
- 9. NP
- 10. NP-hard,NP-난해
- 11. NP-complete,NP-완전
- 12. P-NP 문제
- 13. Kolmogorov complexity
- 14. tmp; cleanup; to mv
- 15. 복잡도 관련 정리들 theorems on/about complexity?
- 16. Links ko
- 17. Links en
- 18. Misc. / Rel.
1. Big O notation ¶
chk 1:
이건 관용적으로 ∈ 자리에 =를 허용해주는 것 같다...?
i.e. 사실은 집합,set 포함 관계로 하면 더 정확한 f(n)∈O(g(n)) 이것을 f(n)=O(g(n))으로 (다들 표기해도 아무 문제없다고 보는 듯) or (그냥 간단히 표기하는 게 대세인듯)
i.e. 사실은 집합,set 포함 관계로 하면 더 정확한 f(n)∈O(g(n)) 이것을 f(n)=O(g(n))으로 (다들 표기해도 아무 문제없다고 보는 듯) or (그냥 간단히 표기하는 게 대세인듯)
chk 2:
O(1) ⊂ O(n) ⊂ ... ⊂ O(n2) ⊂ ... ⊂ O(2n) ...?
O(1) ⊂ O(n) ⊂ ... ⊂ O(n2) ⊂ ... ⊂ O(2n) ...?
두 함수  "$f(n)$")
과  "$g(n)$")
이 주어졌을 때,
모든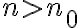
에 대하여,
|\le c|g(n)| "$|f(n)|\le c|g(n)|$")
을 만족하는 두 상수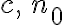 
가 존재하면
=O(g(n)) "$f(n)=O(g(n))$")
이다.
모든
이것은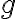 
가 
의 상한값이라는 것이다.
자주 나오는 빅오 표기
| 빅오 | 상한 |
| 빅오메가 | 하한 |
| 빅세타 | ? |
자주 나오는 빅오 표기
| 상수형 | |
| 로그형 | |
| 선형 | |
| 선형로그형 | |
| 2차형 | |
| 3차형 | |
| 지수형 | |
| 팩토리얼형 |
// SNU이광근 컴여세 p100
전제: 입력의 크기
(현재까지) n×n 행렬을 곱하는 가장 빠른 algorithm은 // ,matrix_multiplication
O(n2.3728639) Coppersmith-Winograd
2021-11-14 : seeComputational_complexity_of_matrix_multiplication
n자리 정수 두 개를 빠르게 곱하는 algorithm은 // 곱셈,multiplicationCoppersmith-Winograd2021-11-14 : see
Computational_complexity_of_matrix_multiplication
![[https]](/123/imgs/https.png)
2. Big Ω notation ¶
빅오메가 표기법
{
두 함수 과 이 주어졌을 때,
모든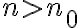 에 대하여,
|\ge c|g(n)| "$|f(n)|\ge c|g(n)|$")
을 만족하는 두 상수 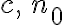가 존재하면
=\Omega(g(n)) "$f(n)=\Omega(g(n))$")
이다.
}
{
두 함수
모든
}
https://mathworld.wolfram.com/Big-OmegaNotation.html
https://xlinux.nist.gov/dads/HTML/omegaCapital.html
https://xlinux.nist.gov/dads/HTML/omegaCapital.html
4. Little o Notation ¶
∀c, ∃n0
such that
f(n) < c g(n) for all n ≥ n0
such that
f(n) < c g(n) for all n ≥ n0
'subquadratic or o(N2) time' (Weiss Java p357)
https://xlinux.nist.gov/dads/HTML/littleOnotation.html
https://mathworld.wolfram.com/Little-ONotation.html
https://mathworld.wolfram.com/Little-ONotation.html
2022-12-24
o(x)에 대해 일단 여기에 임시로 적어놓음 ...
o(x)에 대해 일단 여기에 임시로 적어놓음 ...
later fork to Little_o_notation
rel. Landau_symbol ( https://mathworld.wolfram.com/LandauSymbols.html )
...little o function
rel. Landau_symbol ( https://mathworld.wolfram.com/LandauSymbols.html )
...
little o function//// 이하 김홍종 ////
 "$o(x^n)$")
실수체의 원점 근방에서 정의된 함수 "$f(x)$")
가 =0 "$f(0)=0$")
이고, 어떤 자연수 에 대해
}{x^n}=0 "$\lim_{x\to 0}\frac{f(x)}{x^n}=0$")
이면, 함수 가 원점 근방에서 0으로 수렴하는 정도는 
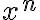이 0으로 수렴하는 정도보다 훨씬 빠르다. 이와 같은 함수 를
| \ll |x^n| "$|f(x)| \ll |x^n|$")
또는
=o(x^n) "$f(x)=o(x^n)$")
또는
\in o(x^n) "$f(x)\in o(x^n)$")
등으로 표시하고, "f 는 (원점 근방에서) o(xn)이다" 또는 "f(x)는 xn보다 절대적으로 아주 작다"고 말한다.
보기를 들면, 어떤 거듭제곱급수(=멱급수,power_series) 함수 "$u(x)$")
에 대하여
 "$\cos x = 1-\frac12 x^2 + x^4 u(x)$")
로 표현되므로
 "$\cos x - 1 + \frac12 x^2 = o(x^3)$")
이다.
실수체의 원점 근방에서 정의된 함수
보기를 들면, 어떤 거듭제곱급수(=멱급수,power_series) 함수
(정리 3.2.2) 다음은 원점 근방에서 정의된 번 미분가능한 함수 가 일 필요충분조건이다:
=0,\; f%27(0)=0,\; \cdots,\; f^{(n)}(0)=0. "$f(0)=0,\; f'(0)=0,\; \cdots,\; f^{(n)}(0)=0.$")
(증명) 만약 =f%27(0)=\cdots=f^{(n-1)}(0)=0 "$f(0)=f'(0)=\cdots=f^{(n-1)}(0)=0$")
이면 로피탈_정리,L_Hopital_s_rule에서
}{x^n} = \lim_{x\to 0} \frac{f%27(x)}{nx^{n-1}} = \cdots = \lim_{x\to 0}\frac{f^{(n-1)}(x)}{n!x} = \frac{f^{(n)}(0)}{n!} "$\lim_{x\to 0} \frac{f(x)}{x^n} = \lim_{x\to 0} \frac{f'(x)}{nx^{n-1}} = \cdots = \lim_{x\to 0}\frac{f^{(n-1)}(x)}{n!x} = \frac{f^{(n)}(0)}{n!}$")
..... (1)
을 얻는다.
따라서=f%27(0)=\cdots=f^{(n-1)}(0)=f^{(n)}(0)=0 "$f(0)=f'(0)=\cdots=f^{(n-1)}(0)=f^{(n)}(0)=0$")
이면
}{x^n} = \frac{f^{(n)}(0)}{n!} = 0, "$\lim_{x\to 0} \frac{f(x)}{x^n} = \frac{f^{(n)}(0)}{n!} = 0,$")
즉
이다. 역으로
=o(x^n) \;\Rightarrow\; f(0)=f%27(0)=\cdots=f^{(n)}(0)=0 "$f(x)=o(x^n) \;\Rightarrow\; f(0)=f'(0)=\cdots=f^{(n)}(0)=0$")
..... (2)
임을 자연수 에 대한 수학적귀납법,mathematical_induction을 써서 밝힌다.
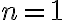일 때에는 이미 앞에서 살펴본 명제이다.
이제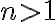
이라고 가정하자. 이면 =o(x^{n-1}) "$f(x)=o(x^{n-1})$")
이고, 따라서 귀납법의 가정( 
번째 명제가 참이라는 가정 )에 의하여
=o(x^{n-1}) \;\Rightarrow\; f(0)=f%27(0)=\cdots=f^{(n-1)}(0)=0 "$f(x)=o(x^{n-1}) \;\Rightarrow\; f(0)=f'(0)=\cdots=f^{(n-1)}(0)=0$")
임을 안다. 그러므로 (1)에서
}{x^n} = \frac{f^{(n)}(0)}{n!} "$0=\lim_{x\to 0}\frac{f(x)}{x^n} = \frac{f^{(n)}(0)}{n!}$")
을 얻는다. 따라서 (2)가 참이다.
따라서
이제
7. P, NP 대략적 설명 ¶
Roughly,
P = the set of all decision problems that are "efficiently solvable"
NP = the set of all decision problems that are "efficiently verifiable"
NPC = { x | x is a decision problem that has the following 2 properties at the same time:
NP = the set of all decision problems that are "efficiently verifiable"
NPC = { x | x is a decision problem that has the following 2 properties at the same time:
(1) x is a member of NP
(2) "all" problems in NP are "efficiently reducible to x }
in Korean(2) "all" problems in NP are "efficiently reducible to x }
P 는 해결이 효율적으로 되는 모든 결정문제들의 집합
NP 는 검증이 효율적으로 되는 모든 결정문제들의 집합
NPC = { x | x 는 다음 두가지 특성을 동시에 만족하는 결정문제,decision_problem:
NP 는 검증이 효율적으로 되는 모든 결정문제들의 집합
NPC = { x | x 는 다음 두가지 특성을 동시에 만족하는 결정문제,decision_problem:
(1) x 는 NP 의 원소
(2) NP 안의 "모든" 문제들은 x 로 효율적으로 reduce 됨 }
(박성빈)(2) NP 안의 "모든" 문제들은 x 로 효율적으로 reduce 됨 }
계산 복잡도 입문 (Linz의 저서 '형식 언어와 오토마타', page 361-374)
http://www.aistudy.com/linguistics/complexity_linz.htm
http://www.aistudy.com/linguistics/complexity_linz.htm
9. NP ¶
NP 는 nondeterministic polynomial (비결정성 다항식) 의 머리 글자
NP_(복잡도){
NP의 뜻: nondeterministic polynomial time.
어떤 문제,problem의 집합,set.
NP에 속하는 문제는 비결정론적_튜링_기계 nondeterministic_Turing_machine (NTM) 로 다항 시간 안에 풀 수 있는 판정문제(결정문제,decision_problem)의 집합.
NP에 속하는 문제는 결정론적_튜링_기계 deterministic_Turing_machine (DTM) 로 다항시간에 검증(무엇을 검증?)이 가능하고, 그 역도 성립.
DTM으로 다항시간안에 풀 수 있는 문제는 NTM으로도 다항시간 안에 풀 수 있으므로, P는 NP의 부분집합. 하지만 P가 NP의 진부분집합인지 여부는 밝혀지지 않음 - P-NP문제,P-NP_problem
}
}
13. Kolmogorov complexity ¶
// Kolmogorov_complexity
만족스럽게도, Kolmogorov complexity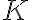
는 근사적으로 Shannon entropy 
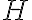와 같다 if the sequence is drawn at random from a distribution that has entropy 
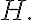그래서 정보,information 이론과 매우 밀접하다.
(p3)
The Kolmogorov complexity of a binary string is defined as the length of the shortest computer program that prints out the string.
(Cover Thomas p6)
Occam's Razor (The simplest explanation is best.)와 관련.
만족스럽게도, Kolmogorov complexity
(p3)
The Kolmogorov complexity of a binary string is defined as the length of the shortest computer program that prints out the string.
(Cover Thomas p6)
Occam's Razor (The simplest explanation is best.)와 관련.
14. tmp; cleanup; to mv ¶
https://mathworld.wolfram.com/AsymptoticNotation.html
https://everything2.com/title/Little o notation
https://everything2.com/title/Landau equivalent
https://everything2.com/title/Little o notation
https://everything2.com/title/Landau equivalent
● 현실적인 알고리듬,algorithm:
복잡도가 입력 크기 의 상수제곱이면 현실적인 algorithm이라고 본다. (polynomial_complexity) - 다항식,polynomial 다항함수,polynomial_function
다항 알고리듬이 있는 문제,problem
상수(>1)의 지수배 제곱. (exponential_complexity) - 지수,exponentiation 지수함수,exponential_function
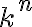
(이광근 컴여세)
복잡도가 입력 크기
≅ 현실적인 비용으로 풀 수 있는 문제
≅ P 클래스 문제
● 비현실적인 algorithm:≅ P 클래스 문제
상수(>1)의 지수배 제곱. (exponential_complexity) - 지수,exponentiation 지수함수,exponential_function
15. 복잡도 관련 정리들 theorems on/about complexity? ¶
See https://complexityzoo.net/Complexity_Dojo
mentions:
Cook-Levin_theorem
Savitch_theorem
Ladner_theorem
Cook-Levin_theorem
Savitch_theorem
Ladner_theorem
16. Links ko ¶
복잡성 이론 complexity theory (2003, essay, 임백준, 행복한 프로그래밍)
http://www.aistudy.com/computer/complexity_lim.htm
mentioned: Hamiltonian_path TSP traveling_salesman_problem
http://www.aistudy.com/computer/complexity_lim.htm
mentioned: Hamiltonian_path TSP traveling_salesman_problem
18. Misc. / Rel. ¶
이름은 비슷. 관계? 차이? 복잡계,complex_system
단어 complex와 complicated 의 의미차? complex complicated difference complex complicated 차이 
complex complicated 차이
complex complicated difference complex complicated 차이 complex complicated 차이
Up: 전산학,compsci