미분,derivative의 정의를 응용.
For 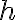 sufficiently close to
sufficiently close to 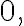
-f(a)}{h}\sim f%27(a))
i.e.
\sim f(a)+f%27(a)h)
ex. 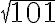 의 근사값은?
의 근사값은?
sol.)
=\sqrt{x})
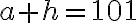
여기서 a는 함수에 넣었을 때 계산하기 편한 것으로, h는 위에서 말했듯 0에 가까운 것으로 정한다. 그리하여
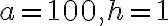
따라서
+f%27(100)\cdot 1)
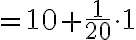
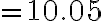
이것은 참값 10.049875…와 비슷.
sol.
위에서 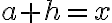 라고 하면,
라고 하면,
For sufficiently close to
sufficiently close to 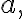
\sim f(a)+f%27(a)(x-a))
여기서 ~의 우측은 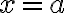 에서 접선의 방정식. 이것을 선형근사(linear approximation)나 선형화(linearization)라고 하며
에서 접선의 방정식. 이것을 선형근사(linear approximation)나 선형화(linearization)라고 하며  대신 L과 등호를 써서 다음과 같이 나타냄.
대신 L과 등호를 써서 다음과 같이 나타냄.
 = f(a)+f%27(a)(x-a))
가정:  는 미분가능.
는 미분가능.
For
또한
=f(a)+f%27(a)(x-a))
를 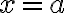 에서
에서  의 선형화(linearization)라고 함.
의 선형화(linearization)라고 함.
Examples: Go to 선형화,linearization.
미분,differential을 쓴 표현 ¶

강우석 2021-03-10 25m
multivariable case ¶
지난 시간에 본 접평면,tangent_plane의 방정식은
(x-x_0)+f_y(x_0,y_0)(y-y_0))
였고 이를 이용하여 선형근사에 대해 알아본다.
) 에 대하여
에 대하여
\approx(a,b)) 이면
이면
\approx L(x,y)=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b))
이고, 이를 ) 에서
에서  의 선형화,linearization라 한다.
의 선형화,linearization라 한다.
- 선형근사(함수)
- 일차근사(함수)
- 접평면근사(함수)
2변수 함수의 선형근사식
일반적으로 (접평면,tangent_plane 식으로부터) 점 )) 에서 이변수함수
에서 이변수함수  의 그래프에 대한 접평면의 방정식은 다음과 같다.
의 그래프에 대한 접평면의 방정식은 다음과 같다.
+f_x(a,b)(x-a)+f_y(a,b)(y-b))
이 접평면의 방정식을 그래프로 갖는 선형함수는 다음과 같다.
=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b))
이 식을 ) 에서
에서  의 선형화,linearization라 하고,
의 선형화,linearization라 하고,
다음과 같은 근사식을) 에서
에서  의 선형근사(linear appoximation) 또는 접평면근사,tangent_plane_approximation라고 한다.
의 선형근사(linear appoximation) 또는 접평면근사,tangent_plane_approximation라고 한다.
\approx f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b))
(Stewart 8e ko p771)
다음과 같은 근사식을
(삼변수함수)
) 이면, 선형근사는
이면, 선형근사는
\approx f(a,b,c)+f_x(a,b,c)(x-a) + f_y(a,b,c)(y-b) + f_z(a,b,c)(z-c))
그리고 선형화 ) 는 위 식의 우변.
는 위 식의 우변.
(Stewart 8e ko p775)
Etc ¶
기호 ≈ (U+2248)
정의에서 미분,derivative과 관련.
선형근사의 아이디어는 미분,differential의 용어(terminology)와 표기법(notation)으로 공식화되어 있음(formulated).
원문: The ideas behind 선형근사,linear_approximations are sometimes formulated in the terminology and notation of differentials.
{
 가 미분가능한 함수이고
가 미분가능한 함수이고 ) 이면 디퍼렌셜/미분
이면 디퍼렌셜/미분 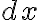 는 독립변수다. (어떤 실수 값도 가질 수 있다.)
는 독립변수다. (어떤 실수 값도 가질 수 있다.)
그러면 디퍼렌셜/미분 (정확히는 전미분)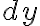 는
는 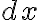 에 대해 다음 식으로 정의된다.
에 대해 다음 식으로 정의된다.
\,dx)
}
정의에서 미분,derivative과 관련.
선형근사의 아이디어는 미분,differential의 용어(terminology)와 표기법(notation)으로 공식화되어 있음(formulated).
원문: The ideas behind 선형근사,linear_approximations are sometimes formulated in the terminology and notation of differentials.
{
그러면 디퍼렌셜/미분 (정확히는 전미분)
QQQ CHK
테일러_급수,Taylor_series의 n항까지의 합은 선형근사를 더 많은 항을 써서 더 정확히 근사하는 방법, 선형근사의 일반화, 인지?
테일러 급수 그 자체는 근사가 아니고 완벽히 정확한 것?
식 비교. 선형근사:
\approx f(a)+f%27(a)(x-a))
테일러 급수의 n항까지의 합:
\approx f(a)+f%27(a)(x-a)+\frac{f%27%27(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n)
테일러 급수:
=f(a)+f%27(a)(x-a)+\frac{f%27%27(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n + \cdots)
(위 둘은 근사식 - 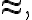 아래 하나는 등식 -
아래 하나는 등식 -  )
)
테일러_급수,Taylor_series의 n항까지의 합은 선형근사를 더 많은 항을 써서 더 정확히 근사하는 방법, 선형근사의 일반화, 인지?
테일러 급수 그 자체는 근사가 아니고 완벽히 정확한 것?
식 비교. 선형근사:
References
KU김기택
KU김기택

