a>0, b>0일 때, 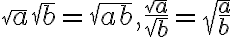 임을 알 고 있을 것이다. ...ⓐ
임을 알 고 있을 것이다. ...ⓐ
이것을 이용하면 다음 두 식이 성립한다. (암기)
이것을 이용하면 다음 두 식이 성립한다. (암기)
a>0, b<0일 경우 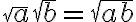 이다.
이다.
a<0, b<0일 경우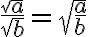 이다.
이다.
ⓒ의 조건은 '모음자양'이라고 외우면 된다.a<0, b<0일 경우
ⓑ의 증명 ¶
전제: 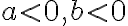
여기서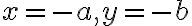 라고 놓는다. 그러면
라고 놓는다. 그러면 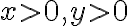 이다. 또한
이다. 또한 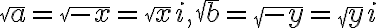 이다.
이다.
여기서
시작
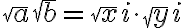 이다. 복소수,complex_number는 곱셈,multiplication의 교환법칙,commutativity이 성립하므로,
이다. 복소수,complex_number는 곱셈,multiplication의 교환법칙,commutativity이 성립하므로,
 인데,
인데,
복소수,complex_number 허수단위,imaginary_unit의 정의에 따라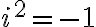 이므로,
이므로,
 ) 이다. ⓐ에 따라
이다. ⓐ에 따라 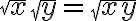 이므로
이므로
(-y)} ) 이다. 위에서 정의한
이다. 위에서 정의한 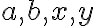 의 관계에 따르면
의 관계에 따르면

복소수,complex_number 허수단위,imaginary_unit의 정의에 따라

