친숙한 알파벳으로 다시 쓰면,
^n)
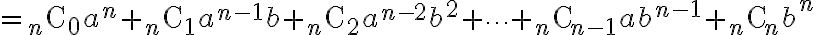
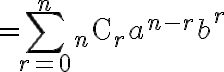
복소수에도 성립
^n=\sum_{\nu=0}^{n}\binom{n}{\nu}a^{\nu}b^{n-\nu})
for 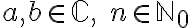
이항계수는\cdots(n-k+1)}{\nu!},\; 1\le \nu \le n) CHK k는 뭐지? 책이 잘못?
CHK k는 뭐지? 책이 잘못?
이항계수는
nCr=nCn-r이므로 대칭형이다.
에
임을 알 수 있다.
from hightop; chk
and
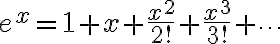
Binomial theorem when  is a positive integer
is a positive integer
 가 실수이고
가 실수이고  이 양의 정수이면
이 양의 정수이면
^n=)
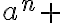
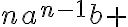
}{2!}a^{n-2}b^2+)
(n-2)}{3!}a^{n-3}b^3+)
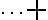
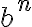
이항계수,binomial_coefficient
!r!})
를 쓰면
^n=\sum_{r=0}^n \binom{n}{r} a^{n-r} b^r)
(Jeffrey AEM 2001 p6)
2022-04-10
이항급수,binomial_series - 급수,series - writing
이항공식,binomial_formula
{
https://planetmath.org/BinomialFormula
공식,formula
}
이항항등식,binomial_identity - 항등식,identity
{
https://mathworld.wolfram.com/BinomialIdentity.html
}
이항급수,binomial_series - 급수,series - writing
이항공식,binomial_formula
{
https://planetmath.org/BinomialFormula
공식,formula
}
이항항등식,binomial_identity - 항등식,identity
{
https://mathworld.wolfram.com/BinomialIdentity.html
}
Twins:
 이항_정리
이항_정리
https://everything2.com/title/Binomial Theorem
https://ghebook.blogspot.com/2010/10/binomial-theorem.html
https://artofproblemsolving.com/wiki/index.php/Binomial_Theorem
https://everything2.com/title/Binomial Theorem
https://ghebook.blogspot.com/2010/10/binomial-theorem.html
https://artofproblemsolving.com/wiki/index.php/Binomial_Theorem
2022-04-09
https://mathworld.wolfram.com/BinomialTheorem.html
https://ncatlab.org/nlab/show/binomial theorem
https://planetmath.org/binomialtheorem
https://proofwiki.org/wiki/Binomial_Theorem
(semi-twin: binomial_series - 급수,series 관점 => https://mathworld.wolfram.com/BinomialSeries.html ... binomial.series )
binomial.series )
https://mathworld.wolfram.com/BinomialTheorem.html
https://ncatlab.org/nlab/show/binomial theorem
https://planetmath.org/binomialtheorem
https://proofwiki.org/wiki/Binomial_Theorem
(semi-twin: binomial_series - 급수,series 관점 => https://mathworld.wolfram.com/BinomialSeries.html ...
Up: 정리,theorem

