기호 m
단위 kg
단위 kg
물체의 운동 상태를 변화시킬 때 물체가 나타내는 저항의 척도. (Zumdahl)
관성 질량(inertial mass)과 중력 질량(gravitational mass)이 있으며, 서로 다른 개념이지만 실험에 의하면 둘은 매우 높은 정밀도로 일치.
관성질량: 힘에 맞서 운동 상태 변화를 거부하는 정도
물체는 속도 변화에 거스르려는 경향을 가짐 (관성,inertia). 그 경향의 정도가 질량.
상대성이론,relativity_theory에서는 정지질량(rest mass, m0) 등을 고려해야 하는데 여기선 논외.
5. 화학: 원자량과 분자량 +질량수 ¶
원자량,atomic_mass
분자량,molecular_mass
이것들은 mass 대신 weight를 쓰기도 한다. 지구 표면에서만 실험을 하는 기초 화학에선 둘 사이에 굳이 구별을 하지 않는 듯 하다.
분자량,molecular_mass
이것들은 mass 대신 weight를 쓰기도 한다. 지구 표면에서만 실험을 하는 기초 화학에선 둘 사이에 굳이 구별을 하지 않는 듯 하다.
질량 = 분자량 × 몰수
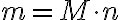
\cdot 1 mol)
원소기호의 왼쪽 위의 첨자형태로 쓰기도 함.
질량수 A = 원자핵,atomic_nucleus 속 (proton수(Z) + neutron수(N)) = baryon수(기호 B, 중입자수, 중입자,baryon 수,  Baryon_number)
Baryon_number)
관계식
원자번호,atomic_number Z { =,atomic_number atomic_number 원자번호 = 핵전하번호 기호 Z ... 원자핵의 전하수. 원자핵 속 양성자의 개수.
atomic_number 원자번호 = 핵전하번호 기호 Z ... 원자핵의 전하수. 원자핵 속 양성자의 개수.  Atomic_number }
Atomic_number }
중성자,neutron 수 N
질량수,mass_number A
사이에는
원자번호,atomic_number Z { =,atomic_number
중성자,neutron 수 N
질량수,mass_number A
사이에는
Z = A − N관계가 있음.
N = A − Z
7. 질량중심 center of mass ¶
대충,
물체의 질량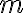 이 각 입자 질량의 합
이 각 입자 질량의 합 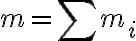 이고
이고
그 위치가,\,(x_2,y_2,z_2),\,\cdots) 이면
이면
질량중심의 x좌표는
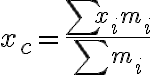
질량중심의 y좌표는
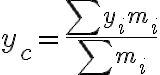
(z 좌표도 마찬가지, 생략)
이렇게 되는듯.
물체의 질량
그 위치가
질량중심의 x좌표는
이렇게 되는듯.
설명:
(참조: physica.gsnu.ac.kr 물리의 이해 > 힘과 운동 > 운동량과 충돌 > 입자계외 질량중심)
i.e.
질량밀도,density와 조금 관련 (계산할 때 서로가 언급될 수 있던데...)
8. 미적분 관점 ¶
3차원 공간에 있는 영역  를 채우고 있는 물체의 밀도함수,density_function(rel. 밀도,density, 확률밀도함수,probability_density_function,PDF)를
를 채우고 있는 물체의 밀도함수,density_function(rel. 밀도,density, 확률밀도함수,probability_density_function,PDF)를 ) 라 하면,
라 하면,
 위에서
위에서 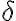 의 적분값이 질량(mass)이다.
의 적분값이 질량(mass)이다.
좌표평면에 관한 입체  의 1차 모멘트(first_moment, curr see 모멘트,moment)는 평면에서 점
의 1차 모멘트(first_moment, curr see 모멘트,moment)는 평면에서 점 ) 까지의 거리에 그 점에서 입체의 밀도를 곱하고
까지의 거리에 그 점에서 입체의 밀도를 곱하고  에서 3중적분한 것으로 정의한다. 예를 들어 xy평면에 관한 1차 모멘트는
에서 3중적분한 것으로 정의한다. 예를 들어 xy평면에 관한 1차 모멘트는
\,dV)
이다.
질량중심,mass_center은 1차 모멘트로 얻어진다. 예를 들면 질량중심의 x 성분은 이다.
이다.
얇고 평평한 판과 같은 2차원 물체의 경우 1차 모멘트는 간단히 z성분을 누락하여 얻을 수 있다. 그래서 y축에 대한 1차 모멘트는 y축으로부터의 거리에 밀도를 곱하여 적분하는 것으로 다음과 같다.
\,dA)
(요약)
2차원 평평한 판의 경우
3차원 입체의 경우
질량중심,mass_center은 1차 모멘트로 얻어진다. 예를 들면 질량중심의 x 성분은
얇고 평평한 판과 같은 2차원 물체의 경우 1차 모멘트는 간단히 z성분을 누락하여 얻을 수 있다. 그래서 y축에 대한 1차 모멘트는 y축으로부터의 거리에 밀도를 곱하여 적분하는 것으로 다음과 같다.
2차원 평평한 판의 경우
3차원 입체의 경우
질량:
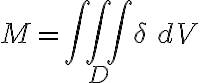 .....
..... ) 는
는 ) 에서 밀도함수
에서 밀도함수
좌표평면에 관한 1차 모멘트:
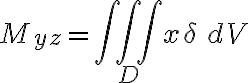
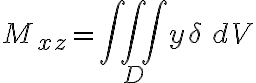
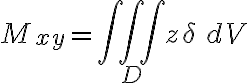
질량중심:
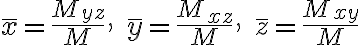
(Thomas 13e ko chap13.6 모멘트와 질량중심)
