편도함수를 구한다 = 편미분한다
2. Clairaut's theorem ¶
f(x, y)가 점 (a, b) 주변의 모든 점에서 fxy, fyx가 존재하고 연속이면
see also (short) 아래 '수학백과: 편미분'의 4.편미분 교환법칙
비슷한 느낌의 정리가 푸비니_정리,Fubini_theorem
4. 연쇄법칙,chain_rule ¶
1변수의 경우,
Leibniz's notation으로는
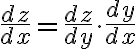
Leibniz's notation으로는
2변수라면?
,)
,\; y=h(t)) : 미분가능
: 미분가능
,h(t)),\; t\mapsto z)
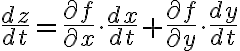
그리고...
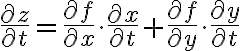
cleanup
Notation:

이것은
}=\frac{\partial z}{\partial(x,y)}\frac{\partial(x,y)}{\partial(s,t)})
"Jacobian matrix"
see 야코비안,Jacobian
6. etc ¶
Related:
Compare:
{
https://ncatlab.org/nlab/show/partial differentiation
}
Zill 표지 적분표에 이런게 있는데 뜻/유도법/활용예/외울가치있는지??
Compare:
{
https://ncatlab.org/nlab/show/partial differentiation
}
Zill 표지 적분표에 이런게 있는데 뜻/유도법/활용예/외울가치있는지??
38. dt=\int_a^b\frac{\partial}{\partial x}g(x,t)dt)
=> 2023-05-13 이것의 이름은 라이프니츠_적분규칙,Leibniz_integral_rule
Twins:
![[https]](/123/imgs/https.png) 수학백과: 편미분
수학백과: 편미분
![[https]](/123/imgs/https.png) 수학백과: 편도함수
수학백과: 편도함수
https://planetmath.org/partialderivative
https://mathworld.wolfram.com/PartialDerivative.html
 Partial_derivative
Partial_derivative
 편미분
편미분
![[https]](/123/imgs/https.png) 수학백과: 편미분
수학백과: 편미분![[https]](/123/imgs/https.png) 수학백과: 편도함수
수학백과: 편도함수https://planetmath.org/partialderivative
https://mathworld.wolfram.com/PartialDerivative.html
각각 x축 y축 방향만으로의 기울기,slope를 의미하는지? CHK
2023-11-18
편미분,partial_differentiation과 편도함수,partial_derivative로 나누는 건 어떨지? (mkl 도함수,derivative)
 Define: partial differentiation
Define: partial differentiation
편미분,partial_differentiation과 편도함수,partial_derivative로 나누는 건 어떨지? (mkl 도함수,derivative)
----
- [1] 수학백과: 편미분

