표준정규분포,standard_normal_distribution

평균이 0, 표준편차가 1인 정규분포. 따라서
$\mathrm{N}(0,1)$
로 표기.


N(0,1)을 따르는 확률변수 Z의 확률밀도함수는 (정규분포 곡선에 m=0과 σ=1을 대입하여)
$f(z)=\frac1{\sqrt{2\pi}}e^{-\frac{z^2}2}$
임.

정규분포 N(m,σ²)을 따르는 확률변수 X를,
표준정규분포 N(0,1)을 따르는 확률변수 Z로
바꾸는 것을 표준화라고 함.

$P(x_1\le X\le x_2)$
$=P\left(\frac{x_1-m}\sigma \le \frac{X-m}\sigma \le \frac{x_2-m}\sigma\right)$
$=P\left(\frac{x_1-m}\sigma \le Z \le \frac{x_2-m}\sigma\right)$

다시 말해,
X~N(m,σ²)일 때 Z=(X-m)/σ는
Z~(0,1)

i.e.
정규분포의 pdf
$f(x)=\frac1{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
에 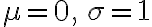$\mu=0,\,\sigma=1$ 을 대입하면 표준정규분포의 pdf
$f(x)=\frac1{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$
가 된다.

이항분포,binomial_distribution에서 시행 횟수 n이 커지면 B(n,p)는 근사적으로 N(np, npq)를 따른다.

확률변수 X~B(n,p)이고 n이 충분히 크면, X는 근사적으로 X~N(np,npq)이다.

// ㄷㄱㄱ

어떤 평균과 분산을 가진 정규 분포도 표준 정규 분포로 바뀔 수 있다.

$Z\sim \text{N}(0,1)$

$\sigma Z+\mu \sim \text{N}(\mu, \sigma^2) \;\Leftrightarrow\; \frac{X-\mu}{\sigma} \sim \text{N}(0,1)$

확률변수의 표준화는 확률변수,random_variable#s-4 ("확률변수의 표준화")에서도 언급.
확률변수표준화,random_variable_standardization or standardizing_random_variable { Up: 표준화,standardization }... 라는 page로 fork?