이산확률분포의 일종으로, 발생 가능성이 희박한 사건이 임의의 구간 안에서 평균적으로 λ번 발생할 때, 이 사건이 일어날 횟수의 분포
특정 사건이 발생할 가능성이 매우 드문 경우의 확률분포
- 주어진 시간/길이/넓이/부피 내에 어떤 사건이 일어나는 횟수
- 단위시간/영역에서 정수 값 0, 1, 2, ...을 갖는 사건에 적용
특정 사건이 발생할 가능성이 매우 드문 경우의 확률분포
표기:
=\frac{\lambda^x e^{-\lambda}}{x!}=\frac{e^{-\lambda}\lambda^x}{x!})
pmf 식이 자꾸 헷갈리는데, x가 두번, λ도 두번 등장
X~Pois(np)
)
X가 푸아송 확률변수이고, 모수,parameter가 λ인 확률질량함수,probability_mass_function,PMF f(x)는1. 설명 ¶
// ㄷㄱㄱ week 7-2 0m
Poisson Distribution
Poisson Distribution
이 둘을 계산하는 것은 간단치 않으나, 결과는 간단함을 볼 수 있다.
When 𝛼 events are observed on average, the probability to see 𝑥 events actually
한시간에 평균 손님 열 명이 온다. 9명이 올 확률?
Pr[X=9] = 109 e−10 / 9! ≈ 0.125
Pr[X=9] = 109 e−10 / 9! ≈ 0.125
time slot을 사용해 설명한다...

 이 커지면 Poisson이 되는... - 엄밀히 rewrite
이 커지면 Poisson이 되는... - 엄밀히 rewrite

- 𝛼 events on average over 𝑛 time slots //
time slots 동안 평균
events가 발생.
- Prob. of event occurrence in each slot ~𝛼/𝑛 // 각 slot에서 사건 발생 확률은
- 𝑋: the number of actually observed events //
실제 관측된 사건 수
- When

3.1. from 노경섭 ¶
푸아송분포의 확률함수를 도출하기 위해서,
평균) 과 분산
과 분산 ) 이 모두
이 모두  와 같다는 가정이 필요.
와 같다는 가정이 필요.
 개의 구간에서 발생할 확률은
개의 구간에서 발생할 확률은 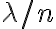
이걸 저 식에 대입하면
=\frac{\lambda^x e^{-\lambda}}{x!})
단위시간당 평균발생 건수는 
) 로 표현.
로 표현.
평균
이걸 저 식에 대입하면
3.2. from 권태원 ¶
확률변수  가 확률밀도함수
가 확률밀도함수
=P(x;\lambda)=\frac{e^{-\lambda}\cdot\lambda^x}{x!})
를 가질 때, 이를 모수가  인 포아송 확률변수라 하고,
인 포아송 확률변수라 하고,
)
로 표기한다.
ex. 매분마다 평균 2건 통화. 3분동안 5건 이상 통화가 이루어질 확률?
=3\times 2=6)
구하는것은=1-P(X\le 4)=)
그렇다면 4건 이하일 확률은
=\sum_{x=0}^4 \frac{e^{-6} 6^x}{x!}) 인데 이것을 계산하다 시간이 다 간다
인데 이것을 계산하다 시간이 다 간다
그러므로 마치 정규분포표가 있듯이 (미리 만들어진) 포아송 누적분포표가 있다, 그것을 쓴다.
 가 6이면서
가 6이면서  가 4 이하일 확률은
가 4 이하일 확률은
=\sum_{x=0}^4 P(x;6)=0.2851)
그래서
=1-P(X\le 4)=1-0.2851=0.7149)
이다. 참고로 X가 특정 값일 확률을 구하는 방법은
=P(X\le 4)-P(X\le 3)=0.2851-0.1512) 이런 식.
이런 식.
구하는것은
그렇다면 4건 이하일 확률은
그러므로 마치 정규분포표가 있듯이 (미리 만들어진) 포아송 누적분포표가 있다, 그것을 쓴다.
그래서
이다. 참고로 X가 특정 값일 확률을 구하는 방법은
3.3. from 이상철 ¶
// https://www.youtube.com/watch?v=gXNat2QEoP0
일정한 공간,space(ex. 일정한 시간,time 단위, 일정한 공간 단위) 내에 발생하는 사건의 개수를 설명.
일정한 공간,space(ex. 일정한 시간,time 단위, 일정한 공간 단위) 내에 발생하는 사건의 개수를 설명.

| 분포 | primary example(?) | 분류 | |
| 푸아송 분포 | 단위시간당 일어난 event의 수 | event의 수는 이산적이니까 | 이산분포 |
| 지수 분포 | event 사이의 시간 | 시간은 연속적이니까 | 연속분포 |
수식
R로는 //// 나중에 ref 찾아보고 확실히 ... d와 p의 뜻?
# P(X=a) 확률 계산 dpois(X=..., lambda=...) # P(X <= 1) 이하로 받을 확률 etc ppois(q=1, lambda=..., lower.tail = (TRUE or FALSE))
3.5. 포아송 확률 변수 Poisson random variable ¶
이하 from http://www.kocw.net/home/search/kemView.do?kemId=1279832 8. Conditional Probability, Independence of Events, Sequential Experiments 16:00~
Up: 확률변수,random_variable - 저 페이지에 성대 강의 받아적은 거 있음.
정의. Let random variable 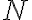 : number of occurrences of an event in a certain time period (or in a certain space.)
: number of occurrences of an event in a certain time period (or in a certain space.)
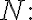 the Poisson random variable with pmf
the Poisson random variable with pmf
=P_N(k)=\frac{\alpha^k}{k!}e^{-\alpha},\quad\quad k=0,1,2,\cdots)
where
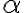 : the average number of event occurrences in a specified time interval (시간 내, 평균 발생 횟수)
: the average number of event occurrences in a specified time interval (시간 내, 평균 발생 횟수)
Note
(1)
=\sum_{k=0}^{\infty}\frac{\alpha^k}{k!}e^{-\alpha}=e^{-\alpha}\sum_{k=0}^{\infty}\frac{\alpha^k}{k!}=1.)
(2)
=\sum_{k=0}^{\infty}k\cdot P_N(k))
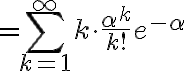
!})
!})


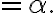
이리하여 분산이 평균과 같다는 특징이 있다.
(3)
콜센터에서 t초 내에 도착하는 query의 수가 N인데 푸아송확률변수 with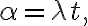
 는 평균 arrival rate(도착률) in queries/second.
는 평균 arrival rate(도착률) in queries/second.
arrival rate가 4 queries/minute라고 한다.
Find the probability of the following events:
(a) more than 4 queries in 10 seconds
(b) fewer than 5 queries in 2 minutes.
(사건은 시간 내에서 랜덤으로 발생한다고 가정.)
⇔ (1)
For 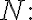 Poisson RV,
Poisson RV,
=\alpha) and
and =\alpha.)
Pf.이리하여 분산이 평균과 같다는 특징이 있다.
For ) is maximum at
is maximum at 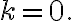
for) is maximum at
is maximum at 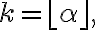 and if
and if 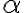 is a positive integer,
is a positive integer,
ex.for
then ) is maximum at
is maximum at 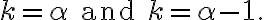
콜센터에서 t초 내에 도착하는 query의 수가 N인데 푸아송확률변수 with
arrival rate가 4 queries/minute라고 한다.
Find the probability of the following events:
(a) more than 4 queries in 10 seconds
(b) fewer than 5 queries in 2 minutes.
sol.
)
(a)
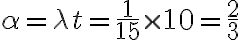
=1-P(N\le 4)=1-\sum_{k=0}^4\frac{(\frac23)^k}{k!}e^{-\frac23}\approx 0.000633 ) in 10(s)
in 10(s)
(a)
(b) 120초 안에 문의가 5개 이하 (less than: 작다, fewer than: 작거나 같다. 라고 강의함)

=\sum_{k=0}^5\frac{8^k}{k!}e^{-8}\approx 0.1)
3.6. 이항확률변수 X와 포아송확률변수 N의 관계 ¶
43:45분
For the binomial r.v. X with the prob. p of a success in n-Bernoulli's trials, when n is very large and p is very small,
이항확률변수 with 확률
with 확률  베르누이 시행에서
베르누이 시행에서  번의 성공....이고, n이 매우 크고 p가 매우 작으면,
번의 성공....이고, n이 매우 크고 p가 매우 작으면,
 fixed, then
fixed, then
={}_n{\rm C}_k p^k (1-p)^{n-k} \;\rightarrow\; P(N=k)=\frac{\alpha^k}{k!}e^{-\alpha})
pf. Since 
=\binom{n}{k}p^k(1-p)^{n-k})
\cdots(n-k+1)}{k!}(\frac{\alpha}n)^k(1-\frac{\alpha}n)^{n-k})
\cdots(n-k+1)}{n^k}\cdot \frac{\alpha^k}{k!} \cdot (1-\frac{\alpha}n)^n \cdot (1-\frac{\alpha}{n})^{-k})
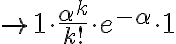
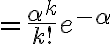
\textrm{ as }n\to\infty.)
52:39
ex.
109 bits/s 의 통신시스템. 비트 에러 확률은 10-9.
Q: 1초에 5개 이상의 오류 발생 확률을 구하라.
이항확률변수
binomial RV X -> Poisson RV N.
i.e. if ex.
109 bits/s 의 통신시스템. 비트 에러 확률은 10-9.
Q: 1초에 5개 이상의 오류 발생 확률을 구하라.
Sol.
여기선 bit error날 확률을 success로 보아야 함에 주의.
Since
 and
and 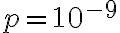 in 1(s),
in 1(s), 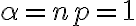 in 1(s).
in 1(s).
=1-P(N\le 4)=1-\sum_{k=0}^4 \frac{1^k}{k!}e^{-1})
\approx0.00366)
On the other hand,
=1-P(X\le4))
^0(1-10^{-9})^{10^9})
^1(1-10^{-9})^{10^9-1})
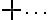
^4(1-10^{-9})^{10^9-4}\}) .....계산하기가 복잡. (Poisson RV가 나온 이유.)
.....계산하기가 복잡. (Poisson RV가 나온 이유.)
ex. n커지고 p작아지면 poisson과 binomial사이의 차이/오류,error가 줄어든다는 예.
제품 불량(defective) 확률이 p1=0.1(p2=0.01).
제품 샘플 수가 n1=10(n2=100)일 때, 최대 한 개의 불량품일 확률을 찾으라.
Find the probability that a sample of n1=..... items contain at most one defective item.
Assume that the quality of successive items is independent.
여기선 bit error날 확률을 success로 보아야 함에 주의.
Since
On the other hand,
제품 불량(defective) 확률이 p1=0.1(p2=0.01).
제품 샘플 수가 n1=10(n2=100)일 때, 최대 한 개의 불량품일 확률을 찾으라.
Find the probability that a sample of n1=..... items contain at most one defective item.
Assume that the quality of successive items is independent.
Sol.
For n1=10 and p1=0.1,
={}_{10}{\rm C}_{0}(\frac9{10})^{10}+{}_{10}{\rm C}_1(\frac1{10})(\frac9{10})^9\approx 0.7361.)
Since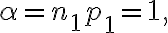
=\sum_{k=0}^1\frac{1^k}{k!}e^{-1}=e^{-1}(1+1)\approx0.7358.)
i.e.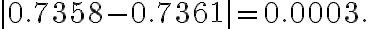
Since
i.e.
For n2=100 and p2=0.01,
={}_{100}{\rm C}_0 (\frac{99}{100})^{100} + {}_{100}{\rm C}_1 (\frac1{100})(\frac{99}{100})^{99}\approx 0.7357.)
i.e.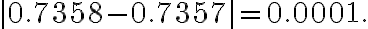
i.e.
3.7. tmp ¶
from http://www.kocw.net/home/search/kemView.do?kemId=1162312 4장_확률변수와분포_포아송분포
{
확률변수 X의 확률질량함수,probability_mass_function,PMF:
=f(x;\mu)=\frac{e^{-\mu}\mu^x}{x!},\quad x=0,1,2,\cdots)
) : 포아송분포의 확률질량함수
: 포아송분포의 확률질량함수
 : 포아송확률변수
: 포아송확률변수 ) ,
,
포아송확률분포의 기대값과 분산:
=\mu)
=\mu)
이항분포와 포아송분포
{
확률변수 X의 확률질량함수,probability_mass_function,PMF:
주어진 단위시간(or 단위영역)에서 발생하는 사건의 횟수.
포아송분포는 발생확률 p가 아주 작아서, 발생평균회수 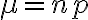 가 작은 사건에 대한 언급.
가 작은 사건에 대한 언급.
i.e.
^{n-x}\,\sim\,\frac{e^{-\mu}\mu^x}{x!})
희소하고 우연한 현상에 적용되는 확률분포임.
n이 크고 확률 p가 작아짐에 따라, 이항분포는 포아송분포와 유사.i.e.
n↑ p↓
예제 1
어떤 항구에 매일 도착하는 유조선: 평균 7척
이 항구의 유조선 수용능력: 10척 / 일
어떤 날 유조선을 외항에 대기시킬 확률은?
Sol.이 항구의 유조선 수용능력: 10척 / 일
어떤 날 유조선을 외항에 대기시킬 확률은?
X: 매일 도착하는 유조선의 수
=1-P(X\le 10)=1-\sum_{x=0}^{10}f(x;7))
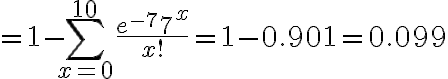
예제 2스캐너 제품 출하시, 1000개당 평균 1개의 불량품
8000개의 제품을 출하할 때 불량품의 개수가 6개 미만일 확률은?
Sol.8000개의 제품을 출하할 때 불량품의 개수가 6개 미만일 확률은?
불량품의 개수가 X라 하면 =B(8000,0.001))
=\sum_{x=0}^5\binom{8000}{x}(0.001)^x(1-0.001)^{8000-x})
이 식은 계산하기 어려우므로 포아송 분포를 사용하면,
\simeq\sum_{x=0}^{5}\frac{e^{-8}8^x}{x!}=0.191)
}이 식은 계산하기 어려우므로 포아송 분포를 사용하면,
4. 푸아송 확률변수 Poisson random variable ¶
푸아송_확률변수,Poisson_random_variable
{
Note in counting the number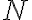 of occurrences of an event in a certain time period or in a certain region in space.
of occurrences of an event in a certain time period or in a certain region in space.
![$P[N=k]=\frac{\alpha^k}{k!}e^{-\alpha}$ $P[N=k]=\frac{\alpha^k}{k!}e^{-\alpha}$](/123/cgi-bin/mimetex.cgi?\Large P[N=k]=\frac{\alpha^k}{k!}e^{-\alpha})
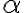 is the average number of event occurrences in a specified time interval or region in space.
is the average number of event occurrences in a specified time interval or region in space.
Let's check the sum of probabilities of all the events
![$\sum_{k=0}^{\infty}P[N=k]=\sum_{k=0}^{\infty}\frac{\alpha^k e^{-\alpha}}{k!}=e^{-\alpha}\sum_{k=0}^{\infty}\frac{\alpha^k}{k!}=e^{-\alpha}\cdot e^{\alpha}=1$ $\sum_{k=0}^{\infty}P[N=k]=\sum_{k=0}^{\infty}\frac{\alpha^k e^{-\alpha}}{k!}=e^{-\alpha}\sum_{k=0}^{\infty}\frac{\alpha^k}{k!}=e^{-\alpha}\cdot e^{\alpha}=1$](/123/cgi-bin/mimetex.cgi?\Large \sum_{k=0}^{\infty}P[N=k]=\sum_{k=0}^{\infty}\frac{\alpha^k e^{-\alpha}}{k!}=e^{-\alpha}\sum_{k=0}^{\infty}\frac{\alpha^k}{k!}=e^{-\alpha}\cdot e^{\alpha}=1)
Note that Poisson pmf is the limiting form of the Binomial pmf when  is very large and the probability of success is kept small; that is,
is very large and the probability of success is kept small; that is,
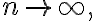 while keeping
while keeping 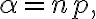 we get the approximation
we get the approximation
^{n-k}\simeq \frac{\alpha^k}{k!}e^{-\alpha})
Proof:
First, consider the probability that no events occur in trials
trials
^n=(1-\frac{\alpha}n)^n\to e^{-\alpha}) as
as 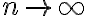
Consider the ratio of successive binomial probabilities
^{n-k-1}}{{}_n{\rm C}_k p^k(1-p)^{n-k}})
p}{(k+1)(1-p)}=\frac{(1-k/n)\alpha}{(k+1)(1-\alpha/n)})
) as
as 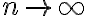
Thus the limiting probabilities satisfy
(\frac{\alpha}{k})\cdots(\frac{\alpha}1)p_0=\frac{\alpha^{k+1}}{(k+1)!}e^{-\alpha})
푸아송_분포,Poisson_distribution 페이지에도 Poisson RV 강의 받아적은 거 있음
}
{
Note in counting the number
is called the Poisson r.v.
- Sample space SX={0, 1, 2, …}
k=0,1,…
- event A of interest is very rare but # of Bernoulli trials is very large
k=0,1,…
First, consider the probability that no events occur in
}


![[https]](/123/imgs/https.png)