완전그래프,complete_graph

Difference between r1.5 and the current

@@ -1,29 +1,50 @@
MKLINK
[[클릭,clique]]
서로 다른 두 꼭짓점,,node,,이 반드시 하나의 변,,edge,,으로 연결된 그래프
참고로 완전그래프는 undirected_graph임.
모든 꼭짓점이 서로 이어진 그래프.[* hz]
WtEn:complete_graph
Sub: [[complete_bipartite_graph]]? chk WtEn:complete_bipartite_graph - [[이분그래프,bipartite_graph]] and [[완전그래프,complete_graph]]? chk
= 채색수, 그래프색칠 문제와의 관계[* hz] =
그래프의 채색수 값이 언제 큰지 쉽게 아는 방법으로, 그래프에 들어있는 '''완전그래프'''를 찾는 방법을 생각해 볼 수 있음.
만약 그래프에 꼭짓점 $k$ 개 짜리 '''완전그래프'''가 들어있다면, 그 $k$ 개는 모두 서로 다른 [[색,color]]이 되어야 하므로, 채색수가 $k$ 이상이어야 하므로, 그래프 $G$ 에 들어있는 가장 큰 '''완전그래프'''의 꼭짓점 수를 $\omega(G)$ 라 하면 다음 부등식이 성립.
$\chi(G)\ge\omega(G)$
[[채색수,chromatic_number]]
[[그래프색칠,graph_coloring]]

TODO moved from clique; merge.
= MKLINK =
[[클릭,clique]]
----
from https://m.blog.naver.com/minichuuuuu/220808115381
{
서로 다른 두 [[꼭짓점node]]이 반드시 하나의 [[변edge]]으로 연결된 그래프
모든 vertex가 직접 adjacent.
그래서 edge의 개수가 정해져 있다.
$n$ 개의 vertex가 있는 '''complete graph'''의 edge 수는 $\frac{n(n-1)}2$
}

참고로 완전그래프는 undirected_graph임.
= tmp bmks ko =
널 그래프와 컴플리트 그래프
https://freshrimpsushi.github.io/posts/null-graph-and-complete-graph/
rel. [[Srch:null_graph]]

----
Compare:
[[완벽그래프,perfect_graph]]는 다른 것임
[[완전트리,complete_tree]]? - [[완전이진트리,complete_binary_tree]] etc

Twins:
https://encyclopediaofmath.org/wiki/Complete_graph
[[WpKo:완전_그래프]]
[[WpEn:Complete_graph]]
https://mathworld.wolfram.com/CompleteGraph.html

Up: [[그래프,graph]]
}
from https://m.blog.naver.com/minichuuuuu/220808115381
{
모든 vertex가 직접 adjacent.
그래서 edge의 개수가 정해져 있다.
$n$ 개의 vertex가 있는 complete graph의 edge 수는 $\frac{n(n-1)}2$
}

References:
hz: https://horizon.kias.re.kr/17681/


서로 다른 두 꼭짓점node이 반드시 하나의 변edge으로 연결된 그래프

참고로 완전그래프는 undirected_graph임.

모든 꼭짓점이 서로 이어진 그래프.[1]



[edit]

채색수, 그래프색칠 문제와의 관계[2]

그래프의 채색수 값이 언제 큰지 쉽게 아는 방법으로, 그래프에 들어있는 완전그래프를 찾는 방법을 생각해 볼 수 있음.
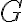만약 그래프에 꼭짓점 $k$ 개 짜리 완전그래프가 들어있다면, 그 $k$ 개는 모두 서로 다른 색,color이 되어야 하므로, 채색수가 $k$ 이상이어야 하므로, 그래프 $G$ 에 들어있는 가장 큰 완전그래프의 꼭짓점 수를 $\omega(G)$ 라 하면 다음 부등식이 성립.
$\chi(G)\ge\omega(G)$

채색수,chromatic_number
그래프색칠,graph_coloring

[edit]

MKLINK


from https://m.blog.naver.com/minichuuuuu/220808115381
{
모든 vertex가 직접 adjacent.
그래서 edge의 개수가 정해져 있다.
$n$ 개의 vertex가 있는 complete graph의 edge 수는 $\frac{n(n-1)}2$
}

[edit]

tmp bmks ko

----