상미분방정식,ordinary_differential_equation,ODE

상미분방정식,ordinary_differential_equation,ODE (rev. 1.23)
하나 이상의 unknown function(주로 $y, y(x), y(t)$ 로 표기)의 미분,derivatives을 포함한 미분방정식,differential_equation.


특히 단일 변수에 관하여 하나 또는 그 이상의 종속변수,dependent_variable의 통상도함수(편도함수가 아닌 도함수)만을 포함하는 방정식.

ODE의 order
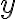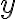ODE가 be of order $n$ 이라는 것: unknown function $y$ 의 $n$ 번째 미분,derivative is the highest derivative of $y$ in the equation
세는 법: of first order, of second order, etc.

따라서 first order ODE의 식은
$F(x,y,y')=0$ (implicit form)
또는
$y'=f(x,y)$ (explicit form)

마찬가지로, General form of nth order ODE:
$F(y,y',y'',\cdots,y^{(n)},x)=0$
다른 표현으로 $F\left(x,y,\frac{dy}{dx},\cdots,\frac{d^ny}{dx^n}\right)=0$ (implicit form)
or
$y^{(n)}=f(y,y',y'',\cdots,y^{(n-1)},x)$ (explicit form)
normal form (Zill)

또는, (wpen)
Implicit form:
$F(x,y,y',\cdots,y^{(n)})=0$
Explicit form:
$F(x,y,y',\cdots,y^{(n-1)})=y^{(n)}$



[edit]

1. MW

[edit]

2. 상미분방정식의 해

구간 $I$ 에서 정의된 함수 $f$ 가 $n$ 번 미분가능하고, $n$ 계 상미분방정식
$F(x,y,y',\cdots,y^{(n)})=0$
이 있고 $\forall x\in I,$
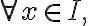
$F(x,f(x),f'(x),\cdots,f^{(n)}(x))=0$
이 성립하면 $f$ 는 구간 $I$ 에서 위 미분방정식의 해이다.

A solution of a given ODE is a relation between 독립변수,independent_variable and 종속변수,dependent_variable which satisfies the given ODE. (최정환)