둘 이상의 독립변수에 대한 unknown function의 편미분을 동반한 미분방정식.
두 개 또는 그 이상의 독립변수,independent_variable에 관하여 하나 또는 그 이상의 종속변수,dependent_variable의 편도함수(편미분,partial_derivative)를 포함하는 방정식.
1.1. The heat equation ¶
1.2. The potential equation AKA Laplace's equation ¶
일 때 퍼텐셜 V는 원점을 제외한 점에서 다음 식을 만족.
2.1. heat eq ¶
열방정식,heat_equation
{
1D: 온도가 제각각인 막대(rod)를 생각
=\alpha\frac{\partial^2T}{\partial x^2}(x,t))
보면 좌변은 온도가 시간에 따라 어떻게 변하는지, 우변은 온도가 공간에 따라 어떻게 변하는지에 대한 것.
(우변은 공간에 대한 second partial derivative에 비례함을 서술함)
3D:
)

여기서 T는 x,y,z,t를 파라미터로 하는 함수임. )
{
1D: 온도가 제각각인 막대(rod)를 생각
보면 좌변은 온도가 시간에 따라 어떻게 변하는지, 우변은 온도가 공간에 따라 어떻게 변하는지에 대한 것.
(우변은 공간에 대한 second partial derivative에 비례함을 서술함)
1D에서 온도 변화에 대해 생각.
from https://youtu.be/ly4S0oi3Yz8?t=496 (3Blue1Brown의 DE 동영상 2: PDE관련)
어떤 점보다 그 주변(neighbor)의 평균 온도가 높다면 온도가 올라가고, 낮다면 온도가 내려갈 것이다.
문제를 간단하게 만들기 위해 (연속적이 아닌) 이산적인 1D 공간을 가정하고, 이웃하는 세 점을 생각하고, 주변은 양쪽 두 곳만 본다.
공간의 점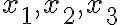 가 연달아 있고, 그 점에서 온도가 각각
가 연달아 있고, 그 점에서 온도가 각각 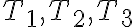 이다.
이다.
주변 온도 평균은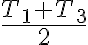 이다.
이다.
그래서) 가 양이면 뜨거워지고(heat up), 음이면 식을 것이다(cool down). 차이,difference가 클수록 빨리.
가 양이면 뜨거워지고(heat up), 음이면 식을 것이다(cool down). 차이,difference가 클수록 빨리.
)
-(T_2-T_1) \right))
이렇게 약간의 조작을 가하면 이것이 차의 차(difference of differences)임을 볼 수 있다. 이 식에서
-(\underbrace{T_2-T_1}_{\Delta T_1}))
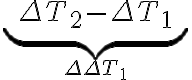
좀 특이하게 보이지만 이렇게 생각하면
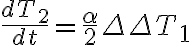
from https://youtu.be/ly4S0oi3Yz8?t=496 (3Blue1Brown의 DE 동영상 2: PDE관련)
어떤 점보다 그 주변(neighbor)의 평균 온도가 높다면 온도가 올라가고, 낮다면 온도가 내려갈 것이다.
문제를 간단하게 만들기 위해 (연속적이 아닌) 이산적인 1D 공간을 가정하고, 이웃하는 세 점을 생각하고, 주변은 양쪽 두 곳만 본다.
공간의 점
주변 온도 평균은
그래서
from https://www.youtube.com/watch?v=ToIXSwZ1pJU (3Blue1Brown의 DE 동영상 3: Solving the heat equation)
나중에
나중에
}
3. 수치적 근사적 해법 ¶
유한요소법,finite_element_method,FEM
{
 유한요소법
유한요소법
 Finite_element_method
Finite_element_method
}
유한차분법,finite_difference_method,FDM
{
미분방정식을 차분방정식으로 근사시켜 컴퓨터로 풀어냄.
공간에서 연속인 지배방정식을 컴퓨터로 풀기 위해서는, 공간을 차분화( 이산화,discretization 이산화
이산화  Discretization )하는 과정이 필요하다.
Discretization )하는 과정이 필요하다.
 Finite_difference_method
Finite_difference_method
{
}
유한차분법,finite_difference_method,FDM
{
미분방정식을 차분방정식으로 근사시켜 컴퓨터로 풀어냄.
공간에서 연속인 지배방정식을 컴퓨터로 풀기 위해서는, 공간을 차분화( 이산화,discretization
PDE뿐만 아니라 ODE에도 쓰인다고 함... 이 내용 relocate... TODO
}4. 간단한 형식으로 써서 몇 PDE 비교 ¶
라플라스_방정식,Laplace_equation
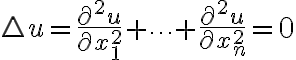
열방정식,heat_equation
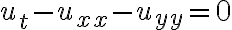
파동방정식,wave_equation
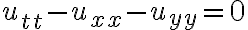
// from https://terms.naver.com/entry.naver?docId=3405384&cid=47324&categoryId=47324 맨밑 참고
Twins:
![[https]](/123/imgs/https.png) 수학백과: 편미분방정식
수학백과: 편미분방정식
http://www.scholarpedia.org/article/Partial_differential_equation
https://everything2.com/title/Partial differential equation
 Partial_differential_equation
Partial_differential_equation
 편미분방정식
편미분방정식
https://encyclopediaofmath.org/wiki/Differential_equation,_partial
https://mathworld.wolfram.com/PartialDifferentialEquation.html
![[https]](/123/imgs/https.png) 수학백과: 편미분방정식
수학백과: 편미분방정식http://www.scholarpedia.org/article/Partial_differential_equation
https://everything2.com/title/Partial differential equation
https://encyclopediaofmath.org/wiki/Differential_equation,_partial
https://mathworld.wolfram.com/PartialDifferentialEquation.html

